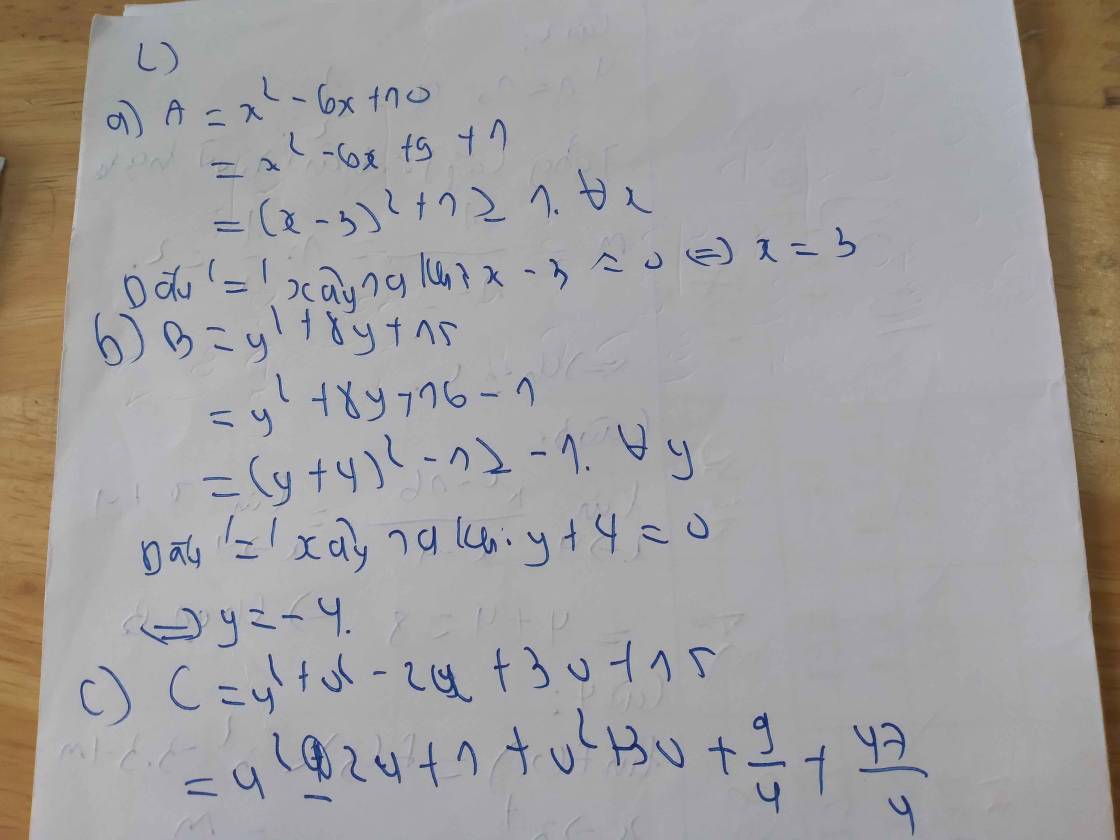Cho x2 +y2 = u2+v2 và xu +yv =0
CMR x2+u2=y2+v2=1 và xy +uv =0

Những câu hỏi liên quan
Dạng 4. Bài Tập Nâng Cao :
Bài 1 : Chứng minh rằng
a, A = 9c2 - 6c + 3 > 0, ∀ c. B = 14m - 6m2 - 13 < 0, ∀ m.
Bài 2. Tìm GTNN của các biểu thức sau
a, A = x2 - 6x + 10. b, B = y2 + 8y + 15.
c, C = u2 + v2 - 2u + 3v + 15 d, D = 2x2 + 5y2 + 4xy + 8x - 4y - 100.
Tìm hai số u và v trong mỗi trường hợp sau: u 2 + v 2 =85,uv =18
Hai số u và v với u 2 + v 2 =85 và uv =18 suy ra : u 2 v 2 =324 nên u 2 và v 2 là nghiệm của phương trình x 2 -85x +324 =0
∆ = - 85 2 – 4.1.324= 7225 – 1296=5929 > 0
∆ = 2959 =77
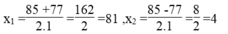
Ta có: u 2 =81 , v 2 =4 suy ra: u = ± 9 ,v= ± 2
hoặc u 2 =4 , v 2 =81 suy ra: u = ± 2 ,v= ± 9
Vậy nếu u=9 thì v=2 hoặc u=-9 ,v=-2
nếu u=2 thì v=9 hoặc u= -2 ,v=-9
Đúng 0
Bình luận (0)
Hãy cho biết phương trình nào dưới đây là phương trình của một đường tròn và tìm tâm, bán kính của đường tròn tương ứng.
a) x2 + y2 + xy + 4x – 2 = 0;
b) x2 + y2 – 2x – 4y + 5 = 0;
c) x2 + y2 + 6x – 8y + 1 = 0.
a) Đây không phải là phương trình đường tròn do có \(xy\).
b) Vì \({a^2} + {b^2} - c = {1^2} + {2^2} - 5 = 0\)nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {4^2} - 1 = 24 > 0\)nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;4} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = 2\sqrt 6 \).
Đúng 0
Bình luận (0)
Tìm u và v trong mỗi trường hợp sau: u2+v2=13, uv=16
Giúp mik vs các bn ơi huhuhu :(((
\(\left\{{}\begin{matrix}u^2+v^2=13\\uv=16\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}u^2+v^2=13\\u^2v^2=256\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}u^2=13-v^2\\\left(13-v^2\right)v^2=256\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}u^2=13-v^2\\13v^2-v^4-256=0\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}u^2=13-v^2\\v^4-13v^2+256=0\left(1\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow\) v4 - 2.\(\dfrac{13}{2}\)v2 + \(\dfrac{169}{4}\) + \(\dfrac{855}{4}\) = 0
\(\Leftrightarrow\) (v2 - \(\dfrac{13}{2}\))2 + \(\dfrac{855}{4}\) = 0 (Vô nghiệm)
\(\Rightarrow\) Pt vô nghiệm
\(\Rightarrow\) Hpt vô nghiệm
Chúc bn học tốt!
Đúng 2
Bình luận (0)
Cho x,y >0 và X2 +y2 =8 . Tìm GTLN của xy/xy+1 .
Đặt \(P=\dfrac{xy}{xy+1}\Rightarrow\dfrac{1}{P}=\dfrac{xy+1}{xy}=1+\dfrac{1}{xy}\)
Ta có : \(xy\le\dfrac{x^2+y^2}{2}=\dfrac{8}{2}=4\Rightarrow\dfrac{1}{xy}\ge4\)
\(\Rightarrow\dfrac{1}{P}\ge5\Rightarrow P\le\dfrac{1}{5}\)
Dấu "=" xảy ra khi $x=y=2$
Đúng 2
Bình luận (0)
a) Vẽ hình theo diễn đạt sau đây: Hai đường thẳng mn và pq ko có điểm chung. Đường thẳng xy cắt đường thẳng mn tại điểm U và cắt đường thẳng pq tại điểm V. Biết rằng : góc V1 và U1 là hai góc trong cùng phía: góc U2 và V1 là 2 góc đồng vị: góc V2 và U1 là 2 góc so le trong
b) Khi biết thêm góc U1=V2=360, hãy tìm số đo của các góc V1 và U2
b)
góc V1+góc V2=180 độ
=> V1=góc U2=180 độ-V2=180 độ -36 độ=144 độ
Đúng 0
Bình luận (0)
Cho x>y>2
a.chứng minh x+y>4, xy>4
b. x2 -xy>0, y2 -2y>0, xy-y2>0
a: x>2
y>2
=>x+y>2+2=4
x>y>2
=>xy>2^2=4
b: x^2-xy=x(x-y)
x-y>0; x>0
=>x(x-y)>0
=>x^2-xy>0
y>2
=>y-2>0
=>y(y-2)>0
=>y^2-2y>0
x>y và y>2
=>y>0 và x-y>0
=>y(x-y)>0
=>xy-y^2>0
Đúng 0
Bình luận (0)
1 .cho x + y = 2 và x2 + y2 = 16 . Tính x3 + y3
2. cho x + y = 8 và xy = -20 . Tính x2 + y2 ; x3 + y3 ; và x2 + xy + y2
giúp ạ , cảm cơn
1)
Ta có: x+y=2
nên \(\left(x+y\right)^2=4\)
\(\Leftrightarrow x^2+y^2+2xy=4\)
\(\Leftrightarrow2xy=2\)
hay xy=1
Ta có: \(x^3+y^3\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(=2^3-3\cdot1\cdot2\)
=2
2)\(x^2+y^2=\left(x+y\right)^2-2xy=8^2-2\cdot\left(-20\right)=104\)
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)=8^3-3\cdot\left(-20\right)\cdot8=512+480=992\)
\(x^2+y^2+xy=\left(x+y\right)^2-xy=8^2-\left(-20\right)=64+20=84\)
Đúng 1
Bình luận (0)
Cho x, y là hai số thực thỏa mãn
x
y
+
(
1
+
x
2
)
(
1
+
y
2
)
1.
Chứng minh rằng
x
1
+
y
2
+
y
1
+
x
2...
Đọc tiếp
Cho x, y là hai số thực thỏa mãn x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1. Chứng minh rằng x 1 + y 2 + y 1 + x 2 = 0.
x y + ( 1 + x 2 ) ( 1 + y 2 ) = 1 ⇔ ( 1 + x ) 2 ( 1 + y ) 2 = 1 − x y ⇒ ( 1 + x 2 ) ( 1 + y 2 ) = 1 - x y 2 ⇔ 1 + x 2 + y 2 + x 2 y 2 = 1 − 2 x y + x 2 y 2 ⇔ x 2 + y 2 + 2 x y = 0 ⇔ x + y 2 = 0 ⇔ y = − x ⇒ x 1 + y 2 + y 1 + x 2 = x 1 + x 2 − x 1 + x 2 = 0
Đúng 0
Bình luận (0)