0\(a.S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ 5S=5-5^2+5^3-5^4+.....+5^{99}-5^{100}\\ 5S+S=\left(5-5^2+5^3-5^4+.....+5^{99}-5^{100}\right)+\left(1-5^{ }+5^2-5^3+.....+5^{98}-5^{99}\right)\\ 6S=1-5^{100}\\ S=\dfrac{1-5^{100}}{6}\\ \)

\(b,S6=1-5^{100}\\ 1-S6=5^{100}\) 

=> 5¹⁰⁰ chia 6 du 1

e đang cần gấp, có ai đến giúp e ko?

\(S=1-5+5^2-5^3+...+5^{98}-5^{99}\\ a,S=5^0.\left(1-5\right)+5^2.\left(1-5\right)+...+5^{98}.\left(1-5\right)=-4.\left(5^0+5^2+5^4+...+5^{98}\right)\)

Bài 2: 

Ta có: (x-3)(x+4)>0

=>x>3 hoặc x<-4

Bài 3:

a: \(5S=5-5^2+...+5^{99}-5^{100}\)

\(\Leftrightarrow6S=1-5^{100}\)

hay \(S=\dfrac{1-5^{100}}{6}\)

Đề bài thiếu yêu cầu cụ thể em nhé. em cập nhật lại câu hỏi để được sự hỗ trợ tốt nhất cho tài khoản olm vip

#@₫!%&@^@₫@₫=_++_×%@%@&@@@@=@

Lời giải:

$C=1+5+5^2+5^4+.....+5^{98}+5^{100}$

$25C=5^2C=5^2+5^3+5^4+5^6+....+5^{100}+5^{102}$

$25C-C=(5^3+5^{102})-(5+1)$

$24C=5^{102}-119$

$C=\frac{5^{102}-119}{24}$

a. S = 5 + 5² + 5³ + 5⁴ + 5⁵ + 5⁶ +...+ 5²⁰¹². 

S = (5 + 5² + 5³ + 5⁴) + 5⁵(5 + 5² + 5³ + 5⁴)+....+ 5²⁰⁰⁹(5 + 5² + 5³ + 5⁴)

Vì (5 + 5² + 5³ + 5⁴) = 780 chia hết cho 65

Vậy S chia hết cho 65

b. Gọi số cần tìm là a ta có: (a - 6) chia hết cho 11; (a - 1) chia hết cho 4; (a - 11) chia hết cho 19. 

(a - 6 + 33) chia hết cho 11; (a - 1 + 28) chia hết cho 4; (a - 11 + 38) chia hết cho 19.

(a + 27) chia hết cho 11; (a + 27) chia hết cho 4; (a + 27) chia hết cho 19. 

Do a là số tự nhiên nhỏ nhất nên a + 27 nhỏ nhất

Suy ra: a + 27 = BCNN (4;11; 19).

Từ đó tìm được: a = 809

A = 10ⁿ + 18n - 1 = 10ⁿ - 1 - 9n + 27n

Ta biết số n và số có tổng các chữ số bằng n có cùng số dư khi chia cho 9 do đó  nên 

       * Vậy A chia hết cho 27

a. S = 5 + 5² + 5³ + 5⁴ + 5⁵ + 5⁶ +...+ 5²⁰¹². 

S = (5 + 5² + 5³ + 5⁴) + 5⁵(5 + 5² + 5³ + 5⁴)+....+ 5²⁰⁰⁹(5 + 5² + 5³ + 5⁴)

Vì (5 + 5² + 5³ + 5⁴) = 780 chia hết cho 65

Vậy S chia hết cho 65

b. Gọi số cần tìm là a ta có: (a - 6) chia hết cho 11; (a - 1) chia hết cho 4; (a - 11) chia hết cho 19. 

(a - 6 + 33) chia hết cho 11; (a - 1 + 28) chia hết cho 4; (a - 11 + 38) chia hết cho 19.

(a + 27) chia hết cho 11; (a + 27) chia hết cho 4; (a + 27) chia hết cho 19. 

Do a là số tự nhiên nhỏ nhất nên a + 27 nhỏ nhất

Suy ra: a + 27 = BCNN (4;11; 19).

Từ đó tìm được: a = 809

A = 10ⁿ + 18n - 1 = 10ⁿ - 1 - 9n + 27n

Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:

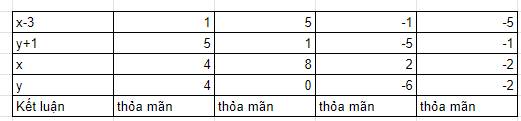
b.

$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$

$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$

$=2+24+(1+5)(5^2+5^4+...+5^{98}$

$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$

$\Rightarrow A$ chia $6$ dư $2$.

1, \(\overline{a45b}\) \(⋮\) 2; 3; 5; 9 

⇒ b = 0; a + 4 + 5 + b ⋮ 9 ⇒ a + 9 ⋮ 9 ⇒ a = 9

Vậy \(\overline{a45b}\) = 9450

2, \(\overline{a1b8}\) \(⋮\) 2;3;9 ⇔ a + 1 + b + 8 ⋮ 9 ⇒ a + b ⋮ 9

⇒ b = 0; 1; 2; 3; 4; 5; 6; 7; 8

     a = 9; 8; 7; 6; 5; 4; 3; 2; 1

\(\Rightarrow\) \(\overline{a1b8}\) = 9108; 8118; 7128; 6138; 5148; 4158; 3168; 2178; 1188

3, 2025 + \(\overline{a36}\) \(⋮\)  3

  ⇔ 2 + 0 + 2 + 5 + a + 3 + 6 ⋮ 3

                    18 + a ⋮ 3 

                             a ⋮ 3 

 a = 0; 3; 6; 9 

4, 125 + 5¹⁰⁰ + \(\overline{31a}\) ⋮ 5

⇔ \(\overline{31a}\) ⋮ 5 

   a ⋮ 5 

   a = 0; 5

1) \(\overline{x45y}⋮2;3;5;9\)

\(\Rightarrow y=0\left(⋮2;5\right)\)

\(x+4+5+0⋮\left(3;9\right)\)

\(\Rightarrow x=9\)

\(\Rightarrow\overline{x45y}=9450\)

3) \(2025+\overline{x36}⋮3\)

mà \(2025⋮3\)

\(\Rightarrow\overline{x36}⋮3\)

\(\Rightarrow x+3+6⋮3\)

\(\Rightarrow x\in\left\{3;6;9\right\}\)

3) \(2022^{10}+4^{20}+\overline{53x}⋮2\)

\(2022^{10}=2022^8.2022^2=\overline{.....6}x\overline{....4}=\overline{.....4}⋮2\)

\(4^{20}=\overline{.....6}⋮2\)

\(\Rightarrow\overline{53x}⋮2\)

\(\Rightarrow x\in\left\{0;2;4;6;8\right\}\)