Cho hàm số \(y = \frac{1}{x}\). Chứng tỏ hàm số đã cho:
a) Nghịch biến trên khoảng \(\left( {0; + \infty } \right)\);
b) Nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Chứng tỏ hàm số \(y = 6{x^2}\) nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
Xét hai số bất kì \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).
Ta có: \(f\left( {{x_1}} \right) = 6x_1^2;f\left( {{x_2}} \right) = 6x_2^2\)
\(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = 6x_1^2 - 6x_2^2\)\( = 6\left( {{x_1} - {x_2}} \right)\left( {{x_1} + {x_2}} \right)\)
\({x_1} < {x_2} \Rightarrow {x_1} - {x_2} < 0\)
\({x_1} < 0;{x_2} < 0 \Rightarrow {x_1} + {x_2} < 0\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0\)
Vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\).
cho hàm số y=f(x)=-x^2-2x+1. Mệnh đề nào sau đây là đúng? A. Hàm số nghịch biến trên khoảng (-1;+vô cực) B. Hàm số nghịch biến trên khoảng (-vô cực;-1) C. Hàm số đồng biến trên khoảng (-1;+vô cực) D. Hàm số đồng biến trên khoảng (-vô cực;0)
B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)
Vẽ đồ thị của các hàm số \(y=3x+1\) và \(y=-2x^2\). Hãy cho biết:
a) Hàm số \(y=3x+1\) đồng biến hay nghịch biến trên R.
b) Hàm số \(y=-2x^2\) đồng biến hay nghịch biến trên mỗi khoảng: \(\left(-\infty;0\right)\) và \(\left(0;+\infty\right)\)
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)

a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Cho hàm số . Trong các khẳng định sau đây, khẳng định nào đúng?
Hàm số đã cho nghịch biến trên nửa khoảng và đồng biến trên nửa khoảng .Hàm số đã cho nghịch biến trên mỗi nửa khoảng , và đồng biến trên khoảng.Hàm số đã cho đồng biến trên mỗi nửa khoảng ;Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
a, chứng tỏ hàm số y = 2x^2 đồng biến khi x > 0; nghịch biến khi x <0
b, chứng tỏ hàm số y = -x^2 đồng biến khi x > 0; nghịch biến khi x <0
a: Khi x>0 thì y>0
=> Hàm số đồng biến
Khi x<0 thì y<0
=> Hàm số nghịch biến
b: Khi x>0 thì y<0
=> Hàm số nghịch biến
Khi x<0 thì y<0
=> Hàm số đồng biến
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Cho hàm số y=f(x) có bảng biến thiên như sau:
A. (1, + 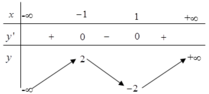
Hàm số đã cho nghịch biến trên khoảng
A. (1, + ∞ )
B. (- ∞ ; -1)
C. (-1,1)
D. (-2,2)
Chọn C
Từ bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng C. (-1,1)
Trong các hàm số sau, hàm số nào đồng biến, hàm số nào nghịch biến trên khoảng xác định của hàm số đó? Vì sao?
a) \(y = {\left( {\frac{{\sqrt 3 }}{2}} \right)^x}\)
b) \(y = {\left( {\frac{{\sqrt[3]{{26}}}}{3}} \right)^x}\)
c) \(y = {\log _\pi }x\)
d) \(y = {\log _{\frac{{\sqrt {15} }}{4}}}x\)
\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)
Hàm số đồng biến là: \(log_{\pi}x\)
Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)