Cho Hình 14, biết ED = EF và EI là tia phân giác của \(\widehat {DEF}\)

Chứng minh rằng:
a) \(\Delta EID = \Delta EIF\)
b) Tam giác DIF cân
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
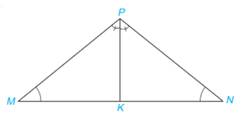
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
Cho \(\Delta ABC\) có \(\widehat{B}\) và \(\widehat{C}\). Vẽ tia phân giác \(\widehat{B}\) cắt AC tại D, vẽ tia phân giác \(\widehat{C}\) cắt AB tại E, BD cắt CE tại F. Chứng minh rằng:
a) BD = CE
b) \(\Delta BEF=\Delta CDF\)
c) AF là tia phân giác của \(\widehat{BAC}\)
Quan sát Hình 6. Vẽ vào tờ giấy tam giác \(DEF\) với \(EF = 4cm,\widehat E = 36^\circ ,\widehat F = 76^\circ \).
a) Chứng minh \(\Delta DEF\backsim\Delta AMC\).
b) Dùng thước đo chiều dài cạnh \(DF\) của \(\Delta DEF\). Tính khoảng cách giữa hia điểm \(A\) và \(C\) ở hai bờ sông trong Hình 6.

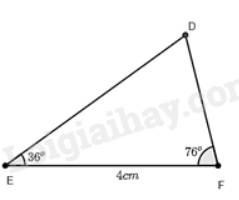
a) Xét tam giác \(DEF\) và tam giác \(AMC\) có:
\(\widehat E = \widehat M = 36^\circ \)
\(\widehat F = \widehat C = 76^\circ \) (chứng minh trên)
Suy ra, \(\Delta DEF\backsim\Delta AMC\) (g.g).
b) Đổi 25m = 2500 cm.
Dùng thước đo độ dài cạnh \(DF\) ta được độ dài \(DF\) là 2,6cm.
Vì \(\Delta DEF\backsim\Delta AMC\) nên \(\frac{{DF}}{{EF}} = \frac{{AC}}{{MC}}\) (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{2,6}}{4} = \frac{{AC}}{{2500}} \Rightarrow AC = \frac{{2,6.2500}}{4} = 1625\).
Vậy khoảng cách giữa hai điểm \(A\) và \(C\) là 1625 cm hay 16,25m.
Cho tam giác DEF cân tại D với đường trung tuyến DI
a) Chứng minh \(\Delta DEI=\Delta DFI\)
b) Cho biết số đo của hai góc DIE và DIF
c) Biết DE = DF = 13 cm, EF = 10 cm. Hãy tính độ dài đường trung tuyến DI ?
a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)
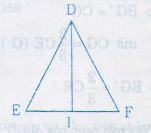
b) Vì ∆DEI = ∆DFI =>
mà = 1800 ( kề bù)
nên = 900
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12
a) ∆DEI = ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
=> ∆DEI = ∆DFI (c.c.c)

b) Vì ∆DEI = ∆DFI => ˆDIE=ˆDIFDIE^=DIF^
mà ˆDIE+ˆDIFDIE^+DIF^ = 1800 ( kề bù)
nên ˆDIE=ˆDIFDIE^=DIF^ = 900
c) I là trung điểm của EF nên IE = IF = 5cm
∆DEI vuông tại I => DI2 = DE2 – EI2 (định lí pytago)
=> DI2 = 132 – 52 = 144
=> DI = 12
Cho tam giác DEF vuông tại D, có DEF=60 độ ,EC là tia phân giác của góc E (C thuộc DF). Từ C, vẽ CH vuông góc EF (H thuộc EF)
a) Chứng minh: tam giác DCE= tam giác HCE
b) Cạnh CH kéo dài cắt tia ED tại K. Chứng minh: tam giác CKF cân tại C
c) chứng minh: DH<CF
a: Xét ΔEDC vuông tại D và ΔEHC vuông tại H có
EC chung
\(\widehat{DEC}=\widehat{HEC}\)
Do đó; ΔEDC=ΔEHC
b: Xét ΔDCK vuông tại D vàΔHCF vuông tại H có
CD=CH
\(\widehat{DCK}=\widehat{HCF}\)
Do đó; ΔDCK=ΔHCF
Suy ra: CK=CF
a, Xét Δ DCE và Δ HCE, có :
EC là cạnh chung
\(\widehat{CDE}=\widehat{CHE}=90^o\)
\(\widehat{DEC}=\widehat{HEC}\) (EC là tia phân giác \(\widehat{DEH}\))
=> Δ DCE = Δ HCE (g.c.g)
=> DC = HC
b, Xét Δ DCK và Δ HCF, có :
DC = HC (cmt)
\(\widehat{DCK}=\widehat{HCF}\) (đối đỉnh)
=> Δ DCK = Δ HCF ( ch - cgn)
=> CK = CF
=> Δ CKF cân tại C
cho tam giác nhọn DEF có DE=DF tia phân giác của góc D cắt EF tại K. Chứng minh:
a/ Tam giác EID bằng tam giác FIK
b/ ED song song với FK
c/Kẻ KX vuông góc với EF tại H trên tia Kx lấy điểm A sao cho HA=HK chứng minh IA=ID
Cho tam giác ABC và điểm M thuộc cạnh BC thỏa mãn \(\Delta AMB = \Delta AMC\)(Hình 32). Chứng minh rằng:
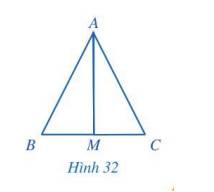
a) M là trung điểm của đoạn thẳng BC.
b) Tia AM là tia phân giác của góc BAC và \(AM \bot BC\).
a) Ta có:\(\Delta AMB = \Delta AMC\)nên AB = AC, MB = MC nên M là trung điểm của đoạn thẳng BC.
b) Ta có:\(\Delta AMB = \Delta AMC\)nên \(\widehat {AMB} = \widehat {AMC},\widehat {MAB} = \widehat {MAC},\widehat {MBA} = \widehat {MCA}\).
Vậy tia AM là tia phân giác của góc BAC vì \(\widehat {MAB} = \widehat {MAC}\).
Ta thấy:\(\widehat {AMB} = \widehat {AMC}\)mà ba điểm B, M, C thẳng hàng nên \(\widehat {BMC} = 180^\circ \).
\(\Rightarrow \widehat {AMB} = \widehat {AMC} = \dfrac{1}{2}.\widehat {BMC} = \dfrac{1}{2}.180^\circ = 90^\circ \). Vậy \(AM \bot BC\).
Cho\(\Delta\)DEF có\(\widehat{EDF}\)=60o, EP là tia phân giác của\(\widehat{DEF}\), FQ là tia phân giác của\(\widehat{DFE}\), PE và FQ cắt nhau tại O.
a) Tính\(\widehat{EOP}\)và chứng minh OP=OQ
b) Tìm điều kiện của\(\Delta\)DEF để P và Q cách đều đường thẳng EF
cho tam giác DEF cân tại D,gọi M là trung điểm EF
a) chứng minh tam giác DEM = tam giác DFM , từ đó chứng minh DM vuông góc EF
b)trên tia đối tia ED lấy điểm K,tia đối của tia FD lấy điểm H sao cho EK=FH.chứng minh tam giác DHK là tam giác cân
c) chứng minh EF // HK
d) gọi I là trung điểm HK .chứng minh D,M,I thẳng hàng
e) chứng minh tam giác HFI = tam giác KEI , từ đó chứng minh tam giác IEF là tam giác cân
f) gọi M là trung điểm EK trên tia đối tia MI lấy điểm N sao cho MI=MN ,chứng minh E,F,N thẳng hàng