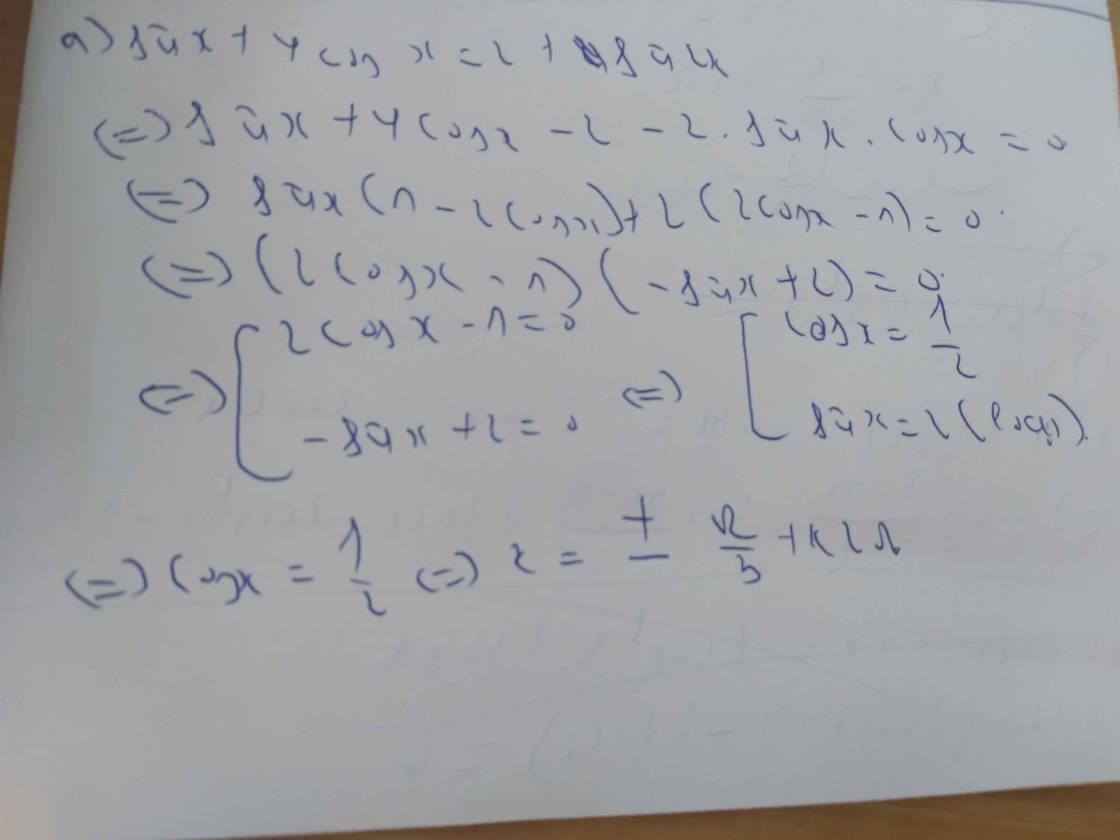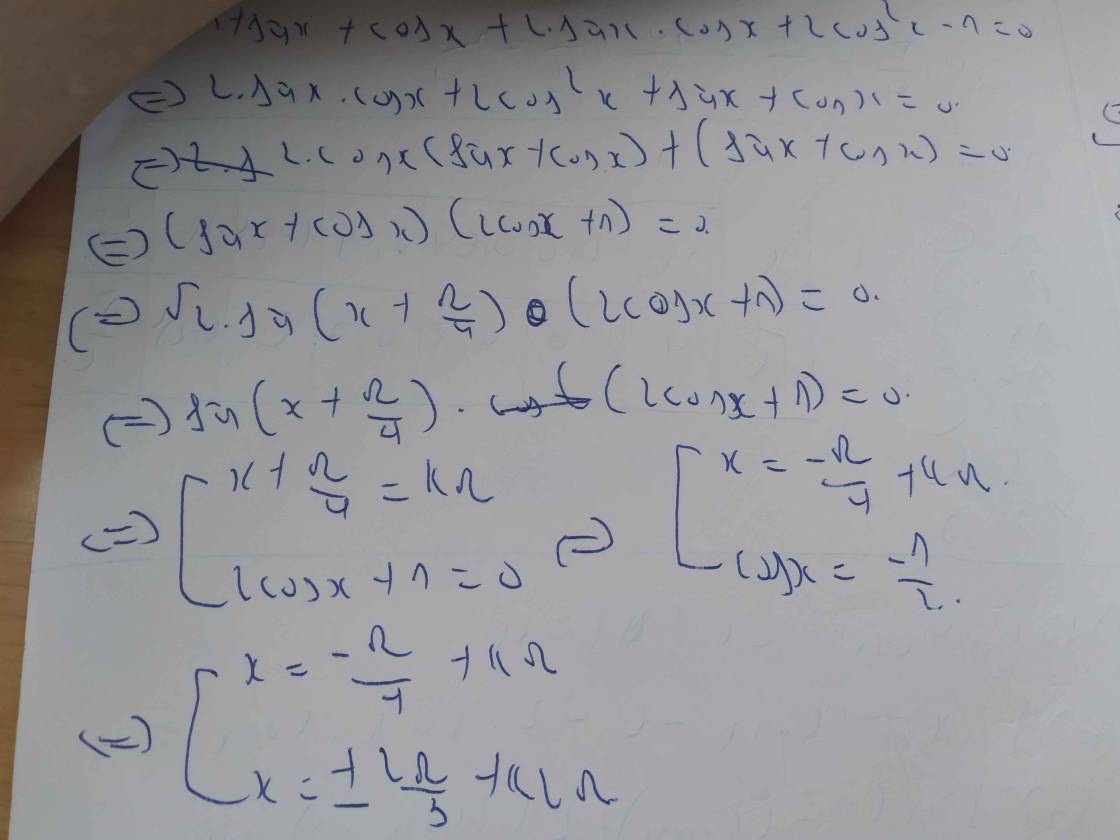1.

\(2sin\left(x+\dfrac{\pi}{6}\right)+sinx+2cosx=3\)

\(\Leftrightarrow\sqrt{3}sinx+cosx+sinx+2cosx=3\)

\(\Leftrightarrow\left(\sqrt{3}+1\right)sinx+3cosx=3\)

\(\Leftrightarrow\sqrt{13+2\sqrt{3}}\left[\dfrac{\sqrt{3}+1}{\sqrt{13+2\sqrt{3}}}sinx+\dfrac{3}{\sqrt{13+2\sqrt{3}}}cosx\right]=3\)

Đặt \(\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)

\(pt\Leftrightarrow\sqrt{13+2\sqrt{3}}sin\left(x+\alpha\right)=3\)

\(\Leftrightarrow sin\left(x+\alpha\right)=\dfrac{3}{\sqrt{13+2\sqrt{3}}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\alpha=arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\\x+\alpha=\pi-arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\end{matrix}\right.\)

Vậy phương trình đã cho có nghiệm:

\(x=k2\pi;x=\pi-2arcsin\dfrac{3}{\sqrt{13+2\sqrt{3}}}+k2\pi\)

2.

\(\left(sin2x+cos2x\right)cosx+2cos2x-sinx=0\)

\(\Leftrightarrow2sinx.cos^2x+cos2x.cosx+2cos2x-sinx=0\)

\(\Leftrightarrow\left(2cos^2x-1\right)sinx+cos2x.cosx+2cos2x=0\)

\(\Leftrightarrow cos2x.sinx+cos2x.cosx+2cos2x=0\)

\(\Leftrightarrow cos2x.\left(sinx+cosx+2\right)=0\)

\(\Leftrightarrow cos2x=0\)

\(\Leftrightarrow2x=\dfrac{\pi}{2}+k\pi\)

\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

Vậy phương trình đã cho có nghiệm \(x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

a/

\(\sqrt{3}sin4x-cos4x=2cosx\)

\(\Leftrightarrow\frac{\sqrt{3}}{2}sin4x-\frac{1}{2}cos4x=cosx\)

\(\Leftrightarrow sin\left(4x-\frac{\pi}{6}\right)=sin\left(\frac{\pi}{2}-x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}4x-\frac{\pi}{6}=\frac{\pi}{2}-x+k2\pi\\4x-\frac{\pi}{6}=\frac{\pi}{2}+x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{2\pi}{15}+\frac{k2\pi}{5}\\x=\frac{2\pi}{9}+\frac{k2\pi}{3}\end{matrix}\right.\)

b/

\(\Leftrightarrow cosx-\sqrt{3}sinx=sin2x-\sqrt{3}cos2x\)

\(\Leftrightarrow\frac{1}{2}cosx-\frac{\sqrt{3}}{2}sinx=\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x\)

\(\Leftrightarrow cos\left(x+\frac{\pi}{3}\right)=sin\left(2x-\frac{\pi}{3}\right)\)

\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(\frac{\pi}{6}-x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{6}-x+k2\pi\\2x-\frac{\pi}{3}=\frac{5\pi}{6}+x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+\frac{k2\pi}{3}\\x=\frac{7\pi}{6}+k2\pi\end{matrix}\right.\)

c/

\(\Leftrightarrow cos3x-\sqrt{3}sin3x=\sqrt{3}cos2x-sin2x\)

\(\Leftrightarrow\frac{1}{2}cos3x-\frac{\sqrt{3}}{2}sin3x=\frac{\sqrt{3}}{2}cos2x-\frac{1}{2}sin2x\)

\(\Leftrightarrow cos\left(3x+\frac{\pi}{3}\right)=cos\left(2x+\frac{\pi}{6}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{3}=2x+\frac{\pi}{6}+k2\pi\\3x+\frac{\pi}{3}=-2x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{6}+k2\pi\\x=-\frac{\pi}{10}+\frac{k2\pi}{5}\end{matrix}\right.\)

hộ vs ae ơi

1.

\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)

\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)

\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)

\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)

\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)

2.

\(\left|cosx-sinx\right|+2sin2x=1\)

\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)

\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)

\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)

3.

\(2sin2x-3\sqrt{6}\left|sinx+cosx\right|+8=0\)

\(\Leftrightarrow2\left(sinx+cosx\right)^2-3\sqrt{6}\left|sinx+cosx\right|+6=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left|sinx+cosx\right|=\sqrt{6}\left(vn\right)\\\left|sinx+cosx\right|=\dfrac{\sqrt{6}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left|sin\left(x+\dfrac{\pi}{4}\right)\right|=\dfrac{\sqrt{3}}{2}\)

\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\pm\dfrac{\sqrt{3}}{2}\)

...

    1 + sinx + cosx + sin2x + cos2x = 0

<=> sin^2x+ cos^2 x + ( sinx+cosx) + 2.sinx.cosx + ( cos^2 x - sin^2 x)=0

<=> 2 cos^2 x + 2sinx.cosx + sinx + cosx =0

<=> 2cosx ( cos x + sinx) + sinx + cosx = 0

<=> ( cosx + sinx ) (2 cos x + 1 ) = 0

<=> cosx + sinx = 0 hoặc 2cosx + 1 =0

1.

\(\Leftrightarrow4sinx.cosx+3\left(sinx-cosx\right)=0\)

Đặt \(sinx-cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\2sinx.cosx=1-t^2\end{matrix}\right.\)

Pt trở thành:

\(2\left(1-t^2\right)+3t=0\)

\(\Leftrightarrow-2t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=2\left(l\right)\\t=-\frac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow sinx-cosx=-\frac{1}{2}\)

\(\Leftrightarrow\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=-\frac{1}{2}\)

\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=-\frac{1}{2\sqrt{2}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+arcsin\left(-\frac{1}{2\sqrt{2}}\right)+k2\pi\\x=\frac{5\pi}{4}-arcsin\left(-\frac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)

2.

Đặt \(sinx-cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sin2x=2sinx.cosx=1-t^2\end{matrix}\right.\)

Pt trở thành:

\(1-t^2-4t=4\)

\(\Leftrightarrow t^2+4t+3=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-3\left(l\right)\end{matrix}\right.\)

\(\Rightarrow sinx-cosx=-1\)

\(\Leftrightarrow\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=-1\)

\(\Leftrightarrow sin\left(x-\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\x-\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\frac{3\pi}{2}+k2\pi\end{matrix}\right.\)

3.

\(\Leftrightarrow1+cosx+sinx+sinx.cosx=2\)

\(\Leftrightarrow2\left(sinx+cosx\right)+2sinx.cosx-2=0\)

Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\2sinx.cosx=t^2-1\end{matrix}\right.\)

Pt trở thành:

\(2t+t^2-1-2=0\)

\(\Leftrightarrow t^2+2t-3=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-3\left(l\right)\end{matrix}\right.\)

\(\Leftrightarrow sinx+cosx=1\)

\(\Leftrightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=1\)

\(\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\frac{\pi}{2}+k2\pi\end{matrix}\right.\)