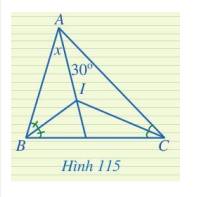
Tìm số đo x trong Hình 115.
bài 58 : tìm số đo x trong hình 40 .hãy giải thích vì sao tính được như vậy ? ?
Do trong hình có 2 đường thẳng cùng vuông góc với một đường thẳng nên 2 đt đó // với nhau
Do đó \(x+115^0=180^0\) (2 góc ở vị trí trong cùng phía)
Vậy \(x=180^0-115^0=65^0\)
vì 2 góc này cùng phía nên tổng bằng 180
có 180-115=65
tìm số đo x trong hình bên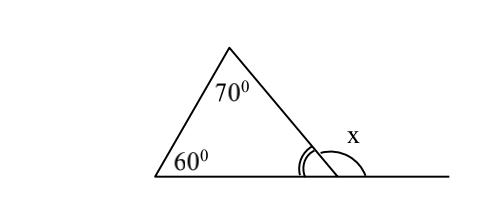
Ta có: △ABC=180o
=> góc C=180o-(70o+60o)=50o
=> C1+C2=180o
=>C2=180o-50o=130o
hay x=130o
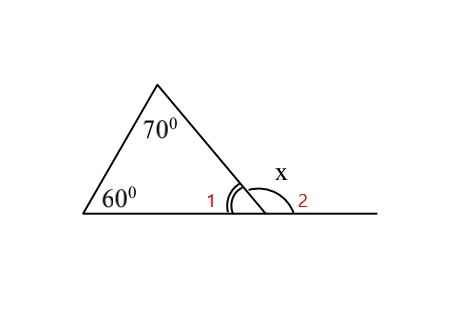
Ta chia \(\widehat{x}:\widehat{x1};\widehat{x2}\)
\(\Rightarrow\widehat{x1}=50^o\)
\(\widehat{x1}+\widehat{x2}=180^o\) (kề bù)
\(\Rightarrow\widehat{x2}=180^o-50^o=130^o\)
tìm số đo x trong hình vẽ
Ta có EMN = 1200
MNF = 600
2 góc này ở vị trí trong cùng phía và EMN + MNF = 1200 + 600 = 1800
=> a//b
Mặt khác, EFN = 900
Mà a//b
=> MEF = 900 (từ vuông góc đến song song)
Vì \(\widehat{EMN}+\widehat{MNF}=120^0+60^0=180^0\) mà 2 góc này ở vị trí trong cùng phía nên a//b
Mà \(b\perp EF\) nên \(a\perp EF\)
Do đó \(x=90^0\)
Tìm số đo x trong Hình 17
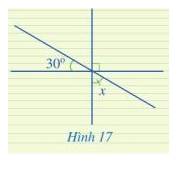
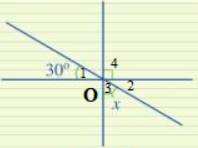
Ta có: \(\widehat {{O_1}} = \widehat {{O_2}}\) ( 2 góc đối đỉnh). Mà \(\widehat {{O_1}} = 30^\circ \Rightarrow \widehat {{O_2}} = 30^\circ \)
Ta có: \(\widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} = 180^\circ \)( kề bù)
\(\begin{array}{l} \Rightarrow x + 30^\circ + 90^\circ = 180^\circ \\ \Rightarrow x = 180^\circ - 30^\circ - 90^\circ = 60^\circ \end{array}\)
Vậy x = 60\(^\circ \)
Tìm số đo x trong hình vẽ sau:
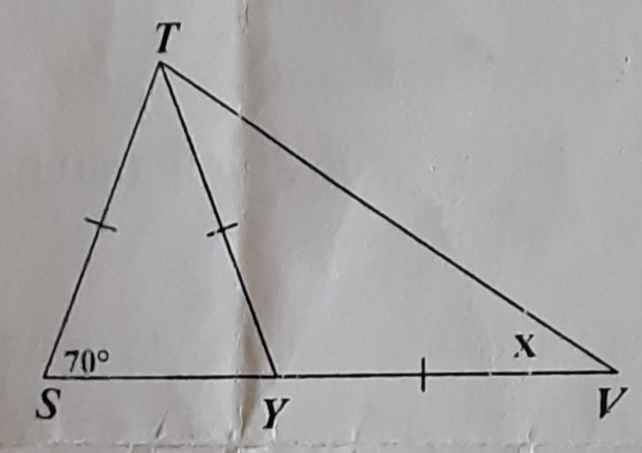
Do tam giác TSY cân tại T \(\Rightarrow\widehat{TSY}=\widehat{TYS}=70^o\)
Mà \(\widehat{TYS}\) là góc ngoài đỉnh Y của tam giác cân TVY
⇒\(2\cdot\widehat{TVY}=\widehat{TYS}=70^o\\ \Rightarrow x=35^o\)
`hat(SYT) = hat(TSY) = 70^o`
`hat(TYV) = 180^o - hat(SYT) = 180^o - 70^o = 110^o`
`=> x = (180^o - 110^o)/2 = 35^o`
Tìm các số đo x, y trong Hình 140.

Tam giác ABO là tam giác đều nên \(\widehat {ABO} = \widehat {AOB} = \widehat {BAO} = 60^\circ \). Vậy \(x = 60^\circ \).
Ba điểm B, O, C thẳng hàng nên \(\widehat {BOC} = 180^\circ \). Mà \(\widehat {AOB} = 60^\circ \)nên \(\widehat {AOC} = 180^\circ - 60^\circ = 120^\circ \).
Xét tam giác AOC có OA = OC. Vậy tam giác AOC cân tại O nên \(\widehat{OAC} = \widehat{OCA} =\dfrac{1}{2}. (180^0-\widehat{AOC})= \dfrac{1}{2}.(180^\circ - 120^\circ ) = 30^\circ \)
Hay \(y = 30^\circ \).
Vậy \(x = 60^\circ \); \(y = 30^\circ \).
Tìm số đo x trong Hình 43, biết u // v
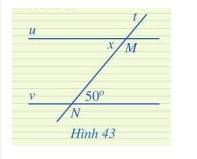
Vì u // v nên x = 50\(^\circ \) ( 2 góc so le trong)
Tìm số đo x của \(\widehat {uOt}\) trong Hình 12.
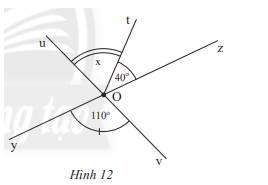
Ta có: \(\widehat {uOz} = \widehat {yOv}\) ( 2 góc đối đỉnh), mà \(\widehat {yOv} = 110^\circ \) nên \(\widehat {uOz} = 110^\circ \)
Mà \(\widehat {uOt},\widehat {tOz}\) là 2 góc kề nhau nên \(\widehat {uOt} + \widehat {tOz} = \widehat {uOz}\)
\(\begin{array}{l} \Rightarrow x + 40^\circ = 110^\circ \\ \Rightarrow x = 110^\circ - 40^\circ = 70^\circ \end{array}\)
Vậy x = 70\(^\circ \)
Trên hình 126, số đo góc MPN nhỏ hơn số đo góc MON là 35 ° . Tổng số đo hai góc MPN và MON là:
(A) 90 °
(B) 105 °
(C) 115 °
(D) 70 °
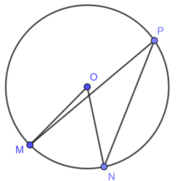
Ta có:
![]() ( góc nội tiếp và góc ở tâm cùng chắn cung nhỏ MN)
( góc nội tiếp và góc ở tâm cùng chắn cung nhỏ MN)
Mà

Đáp án: (B)