Cho a,b,c dương. Chứng minh:
√c(a-c) +√c(b-c) - √ab <=0
Ai giúp hộ mình với,đang cần gấp :v, tks trc
Cho ba số a, b, c dương thỏa mãn a + b + c = 3. Chứng minh rằng: a + b + c ≥ a b + a c + b c
Áp dụng bất đẳng thức Cô – si ta có:
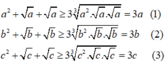
Cộng vế với vế bất phương trình (1), (2), (3) ta được:
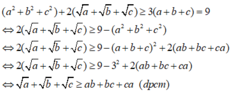
cho a,b,c dương Chứng minh: (a^2 +bc)/(b+c) + (c^2+ab)/(a+b) + (b^2+ac)/(a+c) lớn hơn hoặc bằng a+b+c
cho 3 số dương a,b,c thỏa mãn ab+bc+ca=3.Chứng minh rằng :(a+b)(b+c)(c+a)>=8
Ta có:
\(\left(a+b\right)\left(b+c\right)\left(c+a\right)=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)
\(=\left(a+b+c\right)\left(ab+bc+ca\right)-\sqrt[3]{abc}.\sqrt[3]{ab.bc.ca}\)
\(\ge\left(a+b+c\right)\left(ab+bc+ca\right)-\dfrac{1}{3}\left(a+b+c\right).\dfrac{1}{3}\left(ab+bc+ca\right)\)
\(=\dfrac{8}{9}\left(a+b+c\right)\left(ab+bc+ca\right)\)
Do đó:
\(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge\dfrac{8}{9}.3.\left(a+b+c\right)\ge\dfrac{8}{3}\sqrt{3\left(ab+bc+ca\right)}=8\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=1\)
cho 3 số dương a,b,c thỏa mãn ab+bc+ca=3.Chứng minh rằng :(a+b)(b+c)(c+a)>=8
a+b>=2căn ab
b+c>=2*căn bc
a+c>=2*căn ac
=>(a+b)(b+c)(a+c)>=2*2*2*căn ab*bc*ac=8
Cho ba số thực dương a, b, c . Chứng minh rằng:
\(\dfrac{a^2+bc}{b+c}+\dfrac{b^2+ca}{c+a}+\dfrac{c^2+ab}{a++b}\ge a+b+c\)
\(\dfrac{a^2+bc}{b+c}=\dfrac{\left(a+b\right)\left(a+c\right)-a\left(b+c\right)}{b+c}=\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}-a\)
\(\Rightarrow VT=\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}+\dfrac{\left(a+c\right)\left(b+c\right)}{a+b}-\left(a+b+c\right)\)
Mặt khác áp dụng \(x+y+z\ge\sqrt{xy}+\sqrt{yz}+\sqrt{zx}\)
\(\Rightarrow\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}+\dfrac{\left(a+c\right)\left(b+c\right)}{a+b}\ge a+b+b+c+a+c=2\left(a+b+c\right)\)
\(\Rightarrow VT\ge2\left(a+b+c\right)-\left(a+b+c\right)=a+b+c\) (đpcm)
cho a b c là 3 số dương thoã mãn a+b+c=1 chứng minh rằng:
\(\dfrac{c+ab}{a+b}\)+\(\dfrac{a+bc}{b+c}\)+\(\dfrac{b+ac}{a+c}\)≥2
Đặt vế trái là P
\(P=\dfrac{1.c+ab}{a+b}+\dfrac{1.a+bc}{b+c}+\dfrac{1.b+ac}{a+c}=\dfrac{c\left(a+b+c\right)+ab}{a+b}+\dfrac{a\left(a+b+c\right)+bc}{b+c}+\dfrac{b\left(a+b+c\right)+ac}{a+c}\)
\(P=\dfrac{ac+c^2+bc+ab}{a+b}+\dfrac{a^2+ac+ab+bc}{b+c}+\dfrac{ab+ac+b^2+bc}{a+c}\)
\(P=\dfrac{c\left(a+c\right)+b\left(a+c\right)}{a+b}+\dfrac{a\left(a+c\right)+b\left(a+c\right)}{b+c}+\dfrac{a\left(b+c\right)+b\left(b+c\right)}{a+c}\)
\(P=\dfrac{\left(a+c\right)\left(b+c\right)}{a+b}+\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}\)
Áp dụng BĐT Cô-si:
\(\dfrac{\left(a+c\right)\left(b+c\right)}{a+b}+\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}\ge2\sqrt{\dfrac{\left(a+c\right)\left(b+c\right)\left(a+b\right)\left(a+c\right)}{\left(a+b\right)\left(b+c\right)}}=2\left(a+c\right)\) (1)
Tương tự: \(\dfrac{\left(a+c\right)\left(b+c\right)}{a+b}+\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}\ge2\left(b+c\right)\) (2)
\(\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}\ge2\left(a+b\right)\) (3)
Cộng vế với vế (1);(2);(3):
\(2.\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+2.\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}+2.\dfrac{\left(a+c\right)\left(b+c\right)}{a+b}\ge2\left(a+b\right)+2\left(b+c\right)+2\left(c+a\right)\)
\(\Leftrightarrow\dfrac{\left(a+b\right)\left(a+c\right)}{b+c}+\dfrac{\left(a+b\right)\left(b+c\right)}{a+c}+\dfrac{\left(a+c\right)\left(b+c\right)}{a+c}\ge2\left(a+b+c\right)=2\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
Cho các số dương \(a,b,c\) thoả mãn \(a+b+c=3\). Chứng minh rằng: \(\dfrac{a^2+bc}{b+ca}+\dfrac{b^2+ca}{c+ab}+\dfrac{c^2+ab}{a+bc}\ge3\)
Cho a, b, c là các số dương. Chứng minh rằng a + b c + b + c a + c + a b ≥ 6
Ta có:
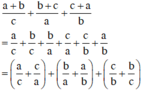
Áp dụng bất đẳng thức Cô-si cho hai số dương
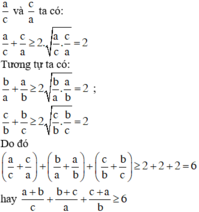
Dấu "=" xảy ra khi và chỉ khi a = b = c
cho a,b,c dương thỏa mãn ab+bc+ca=1. Chứng minh a-b/1+c^2 + b-c/1+a^2 + c-a/1+b^2 = 0