Ta có:
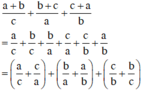
Áp dụng bất đẳng thức Cô-si cho hai số dương
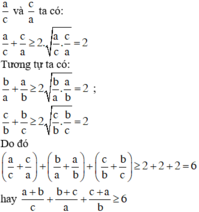
Dấu "=" xảy ra khi và chỉ khi a = b = c
Ta có:
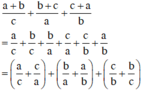
Áp dụng bất đẳng thức Cô-si cho hai số dương
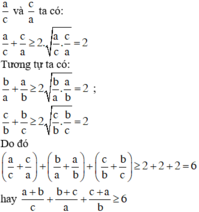
Dấu "=" xảy ra khi và chỉ khi a = b = c
Cho a,b,c là các số thực dương bất kì, chứng minh rằng:
\(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\ge\frac{a+b}{b+c}+\frac{b+c}{a+b}+1\)
Cho a,b,c là các số thực dương thỏa mãn. Chứng minh rằng:
\(\frac{a}{1+b-a}+\frac{b}{1+c-b}+\frac{c}{1+a-c}\ge1\)
Cho $a$, $b$, $c$ là các số dương thỏa mãn $abc = 1$. Chứng minh rằng nếu $a + b + c > \dfrac1a + \dfrac1b + \dfrac1c$ thì có một và chỉ một trong ba số $a$, $b$, $c$ lớn hơn $1$.
Cho a,b,c là các số dương tùy ý, chứng minh rằng:
\(\frac{a^2+b^2}{a+b}+\frac{b^2+c^2}{b+c}+\frac{c^2+a^2}{c+a}\ge\frac{3\left(ab+bc+ca\right)}{a+b+c}\)
Cho a,b,c là các số dương tùy ý. Chứng minh rằng:
\(\frac{\left(a+b+c\right)^3}{abc}+\frac{ab+bc+ca}{a^2+b^2+c^2}\ge28\)
Chứng minh rằng:
(a + 1)(b + 1)(a + c)(b + c) ≥ 16abc, với a, b, c là những số dương tùy ý.
Cho a,b,c là các số thực dương bất kì, chứng minh rằng:
\(\frac{a}{\sqrt{a^2+8bc}}+\frac{b}{\sqrt{b^2+8ca}}+\frac{c}{\sqrt{c^2+8ab}}\ge1\)
Cho ba số a, b, c dương thỏa mãn a + b + c = 3. Chứng minh rằng: a + b + c ≥ a b + a c + b c
Cho a,b,c là các số thực dương thỏa mãn rằng \(a+b+c=3\) . Chứng minh rằng:
\(\left(\frac{a+b}{c}+\frac{b+c}{a}+\frac{c+a}{b}\right)^2\ge4\left(ab+bc+ca\right)\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\)