Tứ giác ABCD có \(\widehat{A}\)= 65o , \(\widehat{B}\)= 117o, \(\widehat{C}\)= 71o. Tính góc ngoài tại đỉnh D.

Những câu hỏi liên quan
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : widehat{A}+widehat{B}200^{^0};widehat{B}+widehat{C}218^0;widehat{C}+widehat{D}160^0 TÍNH widehat{C}VÀ widehat{D}BÀI 2 : CHO TỨ GIÁC ABCD CÓ widehat{B}80^0;widehat{D}120^0GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC BÀI 3 : TỨ GIÁC ABCD CÓ widehat{A}57^0;widehat{C}110^0;widehat{D}75^0.TÍNH GÓC NGOÀI TẠI ĐỈNH B
Đọc tiếp
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : \(\widehat{A}+\widehat{B}=200^{^0};\widehat{B}+\widehat{C}=218^0;\widehat{C}+\widehat{D}=160^0\) TÍNH \(\widehat{C}\)VÀ \(\widehat{D}\)
BÀI 2 : CHO TỨ GIÁC ABCD CÓ \(\widehat{B}=80^0;\widehat{D}=120^0\)GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC
BÀI 3 : TỨ GIÁC ABCD CÓ \(\widehat{A}=57^0;\widehat{C}=110^0;\widehat{D}=75^0\).TÍNH GÓC NGOÀI TẠI ĐỈNH B
Cho tứ giác ABCD có:
\(\widehat{A}=78^o;\widehat{B}=115^o\) góc ngoài tại đỉnh C bằng 102o. Tính D
Gọi góc ngoài đỉnh C là \(\widehat{C}'\)
Ta có: \(\widehat{C}+\widehat{C}'=180^o\)
\(\Rightarrow\widehat{C}=180^o-\widehat{C}'=180^o-102^o=78^o\)
Tổng của bốn góc trong tứ giác là:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Rightarrow\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}+\widehat{C}\right)\)
\(\Rightarrow\widehat{D}=360^o-\left(78^o+115^o+78^o\right)\)
\(\Rightarrow\widehat{D}=89^o\)
Đúng 2
Bình luận (0)
góc C=180-102=78 độ
góc D=360 độ-78 độ-115 độ-78 độ=89 độ
Đúng 1
Bình luận (0)
Tứ giác \(ABCD\) có \(\widehat A = 100^\circ \), góc ngoài tại đỉnh \(B\) bằng \(110^\circ \), \(\widehat C = 75^\circ \). Tính số đo góc \(D\)
Gọi góc ngoài đỉnh B là x
Ta có:
$\widehat {B} + x = 180^0 $
`=>`$ \widehat {B} + 110^0 = 180^0$
`=>` $\widehat {B} = 70^0$
Xét tứ giác ABCD:
$\widehat {A} + \widehat {B} + \widehat {C} + \widehat {D}= 360^0$
`=>` $100^0 + 70^0 + 75^0 + \widehat {D} = 360^0$
`=>` $\widehat {D} = 115^0$
Vậy, $\widehat {D} = 115^0.$
Đúng 1
Bình luận (0)
góc B=180-110=70 độ
góc D=360-100-70-75=115 độ
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có \(\widehat{B}\)=120o,\(\widehat{C}\)=60o,\(\widehat{D}\)=90o.Tính góc A và góc ngoài tại đỉnh A
giúp mik nhe
- Xét tứ giác ABCD:
\(\hat{A}+\hat{B}+\hat{C}+\hat{D}=360\text{°}\)
\(\Rightarrow\hat{A}+120\text{°}+60\text{°}+90\text{°}=360\text{°}\)
\(\Rightarrow\hat{A}=90\text{°}\)
Góc ngoài của đỉnh A \(=360\text{°}-90\text{°}=270\text{°}\)
Đúng 0
Bình luận (0)
Tứ giác ABCD có \(\widehat{A}=65^0,\widehat{B}=117^0,\widehat{C}=71^0\). Tính số đo góc ngoài tại đỉnh D ?
Ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{0}\)(Định lí tổng các góc trong tứ giác)
\(\Rightarrow\)\(\widehat{D}=360^{0}-(\widehat{A}+\widehat{B}+\widehat{C})\)
\(=360^{0}-(65^{0}+117^{0}+71^{0}) =107^{0}\)
Gọi \(\widehat{D_{1}}\) là góc ngoài tại đỉnh D của tứ giác ABCD. Ta có:
\(\widehat{D}+\widehat{D_{1}}=180^{0}\) (\(\widehat{D}\) và \(\widehat{D_{1}}\) là hai góc kề bù)
\(\Rightarrow\) \(\widehat{D_{1}}=180^{0}-\widehat{D}\)
\(=180^{0}-107^{0}=73^{0}\)
Vậy số đo góc ngoài tại đỉnh D của tứ giác ABCD là 730
Đúng 0
Bình luận (0)
Tứ giác ABCD có : \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(65^o+117^o+71^o+\widehat{D}=360^o\)
\(253^o+\widehat{D}=360^o\)
\(\widehat{D}=360^o-253^o=107^o\)
\(\Rightarrow\) Góc ngoài của \(\widehat{D}=180^o-107^o=73^o\)
Vậy số đo góc ngoài tại đỉnh D là \(73^o\)
Đúng 0
Bình luận (0)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^O\) (định lí tứ giác)\
\(\Rightarrow\widehat{D}=360^o-65^o-117^o-71^o\)
\(\Rightarrow\widehat{D}=107^o\)
Gọi \(\widehat{D_1}\) là góc ngoài tại đỉnh D của tứ giác ABCD
\(\Rightarrow\widehat{D}+\widehat{D_1}=180^o\) (kề bù)
\(\Rightarrow\widehat{D_1}=180^o-107^o\)
\(\Rightarrow\widehat{D_1}=73^o\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tứ giác ABCD có\(\widehat{A}=100^0,\widehat{D}=80^0.\) Tia phân giác của góc C và D cắt nhau ở E. Các đường phân giác của góc ngoài tại đỉnh C và D cắt nhau tại F. Tính các góc \(\widehat{CED},\widehat{CFD}\)
Tứ giác ABCD có\(\widehat{A}=110^0,\widehat{B}=100^0\) . Các tia phân giác của các góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau ở F. Tính \(\widehat{CED,}\widehat{CFD}\)
Tứ giác ABCD có \(\widehat{A}=110^0,\widehat{B}=100^0\). Các tia phân giác của các góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau ở F. Tính \(\widehat{CED},\widehat{CFD}\) ?
Tứ giác ABCD có : góc C + góc D = \(360^o\) - ( góc A + góc B )
góc C + góc D = \(360^o\) - ( \(110^o+100^o\) )
góc C + góc D = \(360^o\) - \(210^o\)
góc C + góc D = \(150^o\)
\(\Rightarrow\) Góc \(C_1\) + góc \(D_1\) = \(\dfrac{gocC+gocD}{2}\) = \(\dfrac{150^o}{2}\) = \(75^o\)
Xét \(\Delta CED\) có góc \(C_1\) + góc \(D_1\) + góc CED = \(180^o\) ( Tổng 3 góc của 1 \(\Delta\) )
\(75^o\) + góc CED = \(180^o\)
góc CED = \(180^o\) - \(75^o\)
góc CED = \(105^o\)
Vì DE và DF là các tia phân giác của hai góc kề bù ( gt)
\(\Rightarrow\) DE \(\perp\) DF
Vì CE và CF là các tia phân giác của hai góc kề bù ( gt )
\(\Rightarrow\) CE \(\perp\) CF
Xét tứ giác CEDF co :
góc E + góc ECF + góc EDF + góc F = \(360^o\) ( tổng 4 góc trong 1 tứ giác )
\(105^o+90^o+90^o\)+ góc F = \(360^o\)
góc F = \(360^o\) - ( \(105^o+90^o+90^o\) )
góc F = \(360^o\) - \(285^o\)
góc F = \(75^o\)
Đúng 0
Bình luận (1)
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác
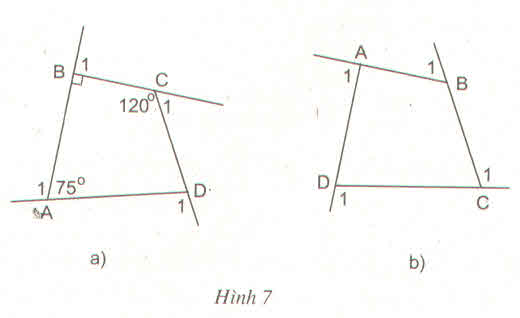
a) Tính các góc ngoài của tứ giác ở hình 7a ?
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài) : widehat{A_1}+widehat{B}_1+widehat{C}_1+widehat{D}_1?
c) Có nhận xét gì về tổng các góc ngoài của tứ giác ?
Đọc tiếp
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác
a) Tính các góc ngoài của tứ giác ở hình 7a ?
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài) : \(\widehat{A_1}+\widehat{B}_1+\widehat{C}_1+\widehat{D}_1=?\)
c) Có nhận xét gì về tổng các góc ngoài của tứ giác ?
Bài giải:
a) Góc ngoài còn lại: 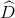 =3600 – (750 + 900 + 1200) = 750
=3600 – (750 + 900 + 1200) = 750
Ta tính được các góc ngoài tại các đỉnh A, B, C, D lần lượt là:
1050, 900, 600, 1050
b)Hình 7b SGK:
Tổng các góc trong  +
+  +
+ +
+ =3600
=3600
Nên tổng các góc ngoài
 +
+  +
+ +
+ =(1800 -
=(1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  )
)
=(1800.4 - ( 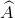 +
+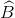 +
+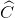 +
+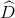 )
)
=7200 – 3600 =3600
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng 3600
Đúng 0
Bình luận (0)
Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Leftrightarrow\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}+\widehat{C}\right)\)
\(\Leftrightarrow\widehat{D}=360^o-\left(90^o+120^o+75^o\right)\)
\(\Leftrightarrow\widehat{D}=360^o-285^o=75^o\)
Ta có:+)\(\widehat{BAD}+\widehat{A_1}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{A_1}=180^o-\widehat{BAD}\)
\(\Rightarrow\widehat{A_1}=180^o-75^o=105^o\)
+)\(\widehat{B}_1+\widehat{CBA}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{B_1}=180^o-\widehat{CBA}\)
\(\Rightarrow\widehat{B_1}=180^o-90^0=90^o\)
\(+)\widehat{C_1}+\widehat{BCD}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{C_1}=180^o-\widehat{BCD}\)
\(\Rightarrow\widehat{C_1}=180^o-120^o=60^o\)
\(+)\widehat{D_1}+\widehat{ADC}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{D}_1=180^o-\widehat{ADC}\)
\(\Rightarrow\widehat{D_1}=180^o-75^o=105^o\)
b,Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}+\widehat{D_1}\)
\(=\left(180^o-\widehat{A}\right)+\left(180^o-\widehat{B}\right)+\left(180^o-\widehat{C}\right)+\left(180^o-\widehat{D}\right)\)
\(=180^o.4-\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)\)
\(=720^o-360^o=360^o\)
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng \(360^o\)
Đúng 0
Bình luận (0)
a)
\(\widehat{A_1}=180^0-75^0=105^0\)|(kề bù)
\(\widehat{B_1}=180^0-90^0=90^0\)(kề bù)
\(\widehat{C_1}=180^0-120^0=60^0\)(kề bù)
\(\Rightarrow\widehat{D}=360^0-\left(\widehat{B_1}+\widehat{C_1}+\widehat{A_1}\right)\)
\(\widehat{D}=360^0-\left(90^0+120^0+75^0\right)\)
\(\leftrightarrow\widehat{D}=75^0\)
\(\Rightarrow\widehat{D_1}=180^0-75^0=105^0\)
b)Xét tứ giác ABCD (hình 7b) có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
Nên tổng các góc ngoài là:
\(\widehat{A}_1+\widehat{B}_1+\widehat{C}_1+\widehat{D}_1=\left(180^0-\widehat{A}\right)+\left(180^0-\widehat{B}\right)+\left(180^0-\widehat{C}\right)+\left(180^0-\widehat{D}\right)\)
\(\Rightarrow180^0.4-\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)\)
\(\Leftrightarrow\widehat{A}_1+\widehat{B}_1+\widehat{C}_1+\widehat{D}_1=720^0-360^0\)
\(\Rightarrow\widehat{A}_1+\widehat{B}_1+\widehat{C}_1+\widehat{D}_1=360^0\)
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng \(360^0\)
Đúng 0
Bình luận (0)



























