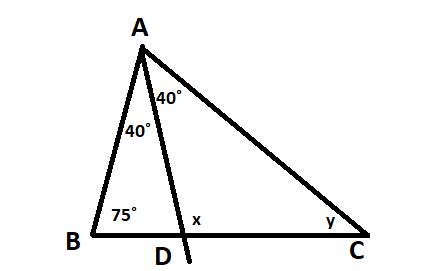
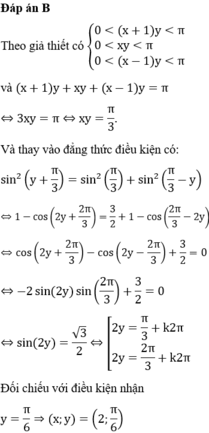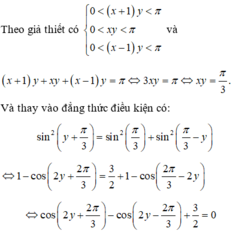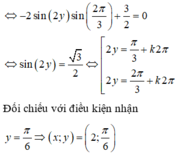Tính số đo x và y
Những câu hỏi liên quan
x/8=y/3 và 2x+3y = 50
Tính X Y
5x=6y và 2x^2 - y^2 = 47
Tính XY
16/11.X=3/2.Y và Y - X =-4
Tính XY
Tính số đo các góc của tam giác ABC. Biết tỷ số giữa số đo góc A cà số đo góc B là 3:4, tỉ số giữa số đo góc B và số đo góc C là 3:5
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{8}=\frac{y}{3}=\frac{2x}{16}=\frac{3y}{9}=\frac{2x+3y}{16+9}=\frac{50}{25}=2\)
Nên : x/8 = 2 => x = 16
y/3 = 2 => y = 6
Vậy x = 16 ; y = 6 .
Đúng 0
Bình luận (0)
Có bao nhiêu cặp số thực (x; y) sao cho (x+1)y, xy và (x-1)y là số đo ba góc một tam giác (tính theo rad) và
sin
2
[
(
x
+
1
)
y
]
sin
2
(
x
y
)
+
sin
2
[
(
x
-
1
)...
Đọc tiếp
Có bao nhiêu cặp số thực (x; y) sao cho (x+1)y, xy và (x-1)y là số đo ba góc một tam giác (tính theo rad) và sin 2 [ ( x + 1 ) y ] = sin 2 ( x y ) + sin 2 [ ( x - 1 ) y ]
A. 4.
B. 1
C. 3.
D. 2.
Đáp án B
Theo giả thiết có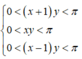 
và
Và thay vào đẳng thức điều kiện có:
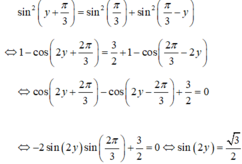
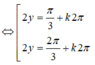
Đối chiếu với điều kiện nhận 
Đúng 0
Bình luận (0)
cho 2 góc kề bù có số đo là x và y tính x;y biết .
A) x;y tỉ lệ thuận với 2 và 3
B) x;y tỉ lệ nghịch với 2 và 3
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{180}{5}=36\)
Do đó: x=72; y=108
Đúng 0
Bình luận (0)
Có bao nhiêu cặp số thực (x; y) sao cho (x+1)y, xy và (x-1)y là số đo ba góc một tam giác (tính theo rad) và
sin
2
x
+
1
y
sin
2
x
y
+
sin
2
x...
Đọc tiếp
Có bao nhiêu cặp số thực (x; y) sao cho (x+1)y, xy và (x-1)y là số đo ba góc một tam giác (tính theo rad) và sin 2 x + 1 y = sin 2 x y + sin 2 x - 1 y
A. 4
B. 1
C. 3
D. 2
câu 5 cho hình vẽ bên biết x//y và M2=125 .Tính số đo các góc m3 ;N1 và N2
Cho biết m // n và a // b. Tính số đo x,y,z và t của các góc trong hình 12.
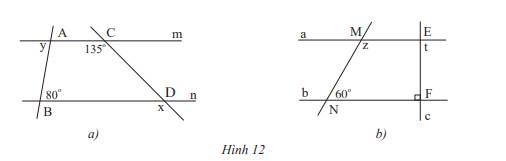
a) Vì m // n nên x = 135\(^\circ \)( 2 góc đồng vị) ; y = 80\(^\circ \) ( 2 góc so le trong)
b)
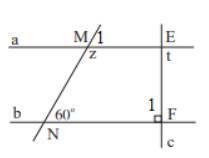
Vì a // b nên \(\widehat {{M_1}} = 60^\circ \) ( 2 góc đồng vị)
Mà \(\widehat {{M_1}} + z = 180^\circ \) ( 2 góc kề bù) nên z = 180\(^\circ \)- 60\(^\circ \)=120\(^\circ \)
Vì a // b nên \(\widehat {{F_1}} = t\) ( 2 góc so le trong), mà \(\widehat {{F_1}} = 90^\circ \) nên t = 90\(^\circ \)
Đúng 1
Bình luận (0)
Có bao nhiêu cặp số thực (x; y) sao cho
x
+
1
y
,
x
y
và
x
-
1
y
là số đo ba góc một tam giác (tính theo rad) và
sin
2
x
+
1
y...
Đọc tiếp
Có bao nhiêu cặp số thực (x; y) sao cho x + 1 y , x y và x - 1 y là số đo ba góc một tam giác (tính theo rad) và sin 2 x + 1 y = sin 2 x y + sin 2 x - 1 y
A. 4.
B. 1.
C. 3.
D. 2.
Tính số đo góc giữa hai đường thẳng \({d_1}:2x--y + 5 = 0\) và\({d_2}:x - 3y + 3 = 0\).
Vecto pháp tuyến của đường thẳng \({d_1}\) là: \(\overrightarrow {{n_1}} = \left( {2; - 1} \right)\)
Vecto pháp tuyến của đường thẳng \({d_2}\) là: \(\overrightarrow {{n_2}} = \left( {1; - 3} \right)\)
Ta có: \(\cos \left( {{d_1},{d_2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.1 + \left( { - 1} \right).\left( { - 3} \right)} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\)
Vậy \(\left( {{d_1},{d_2}} \right) = {45^o}\)
Đúng 0
Bình luận (0)
Cho a// b và x// y như hình vẽ bên. Tính số đo góc x. A.30o B. 60o C. 120o D. 150o
Đọc tiếp
Cho a// b và x// y như hình vẽ bên. Tính số đo góc x.
A.30o B. 60o
C. 120o D. 150o
Xem thêm câu trả lời