Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)

Do đó đề bài xảy ra khi và chỉ khi :

\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)

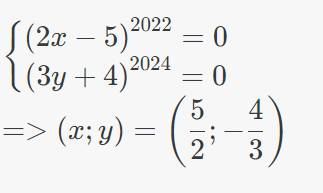Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?

Em xem lại số mũ của 2x - 5y nhé

2023 hay 2024?

\(\left(2x+4\right)^{2024}+\left(\left|3y-9\right|\right)^{2023}=0\) (*) 

Ta có: \(\left(2x+4\right)^{2024}\ge0\forall x\) (vì có số mũ chẵn) (1)

\(\left(\left|3y-9\right|\right)^{2023}\ge0\forall y\) (vì giá trị tuyệt đối luôn ≥0) (2) 

Từ (1) và (2) ta có: 

\(\Rightarrow\left\{{}\begin{matrix}2x+4=0\\3y-9=0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=3\end{matrix}\right.\)

Vậy: ... 

Vì `{(|x - 3y|^2023 >=0), (|y+4|^2024 >=0):} forall x, y`

Nên `{(x=3y), (y = -4):}`

`<=> {(x=-12), (y=-4):}`

=>x-3y=0 và y+4=0

=>y=-4 và x=3y=-12

 |x-3y|^2023 + |y+4|^2024 = 0 

⇒|x-3y| = 0 và |y+4| = 0

⇒x- 3y=0     và    y+4 = 0

                            y     = -4

Vậy, nghiệm của phương trình |x-3y|^2023 + |y+4|^2024 = 0 là x - 3y = 0 và y = -4.

a,Nghiệm của (2\(x\) - 5)²⁰²² là giá trị của \(x\) thỏa mãn

  (2\(x\) - 5)²⁰²² = 0

   2\(x\) -  5 = 0

  2\(x\)        = 5

  2\(x\)       = 5:2

   \(x\)        = 2,5

b, Nghiệm của (3\(x\) + 4)²⁰²⁴ là giá trị của \(x\) thỏa mãn:

(3\(x\) + 4)²⁰²⁴ = 0

    3\(x\) + 4 = 0

    3\(x\)       = -4

   \(x\)       = - 4 : 3

   \(x\) = -\(\dfrac{4}{3}\)

A là giao điểm AB và AC nên tọa độ thỏa mãn:

\(\left\{{}\begin{matrix}2x+y-5=0\\x-3y+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\) \(\Rightarrow A\left(2;1\right)\)

\(d\left(A;...\right)=\dfrac{\left|7.2-8.1+26\right|}{\sqrt{7^2+\left(-8\right)^2}}=\dfrac{32}{\sqrt{113}}\)

a,  7\(x\).(2\(x\) + 10) = 0

        \(\left[{}\begin{matrix}x=0\\2x+10=0\end{matrix}\right.\)

         \(\left[{}\begin{matrix}x=0\\2x=-10\end{matrix}\right.\)

         \(\left[{}\begin{matrix}x=0\\x=-10:2\end{matrix}\right.\)

         \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)

Vậy \(x\in\){-5; 0}

b, - 9\(x\) : (2\(x\) - 10) = 0

      - 9\(x\) = 0

           \(x\) = 0

c, (4 - \(x\)).(\(x\) + 3) = 0

    \(\left[{}\begin{matrix}4-x=0\\x+3=0\end{matrix}\right.\)

    \(\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)

Vậy \(x\in\) {-3; 4}

d, (\(x\) + 2023).(\(x\) - 2024) = 0

    \(\left[{}\begin{matrix}x+2023=0\\x-2024=0\end{matrix}\right.\)

    \(\left[{}\begin{matrix}x=-2023\\x=2024\end{matrix}\right.\)

Vậy \(x\) \(\in\) {-2023; 2024}

\(a\text{) }\left|2x-5\right|+\left|3y+1\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|2x-5\right|=0\\\left|3y+1\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x-5=0\\3y+1=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x=5\\3y=-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
b) \(\left|3x-4\right|+\left|3y-5\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|3x-4\right|=0\\\left|3y-5\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x-4=0\\3y-5=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x=4\\3y=5\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=\dfrac{4}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
c) \(\left|2x-5\right|+\left|xy-3y+2\right|=0\)
\(\Rightarrow\left\{{}\begin{matrix}\left|2x-5\right|=0\\\left|xy-3y+2\right|=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x-5=0\\xy-3y+2=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2x=5\\xy-3y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\xy-3y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\\dfrac{5}{2}y-3y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\\left(\dfrac{5}{2}-3\right)y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\\left(-\dfrac{1}{2}\right)y=-2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=4\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}x=\dfrac{5}{2}\\\left(-\dfrac{1}{2}\right)y=-2\end{matrix}\right.\)