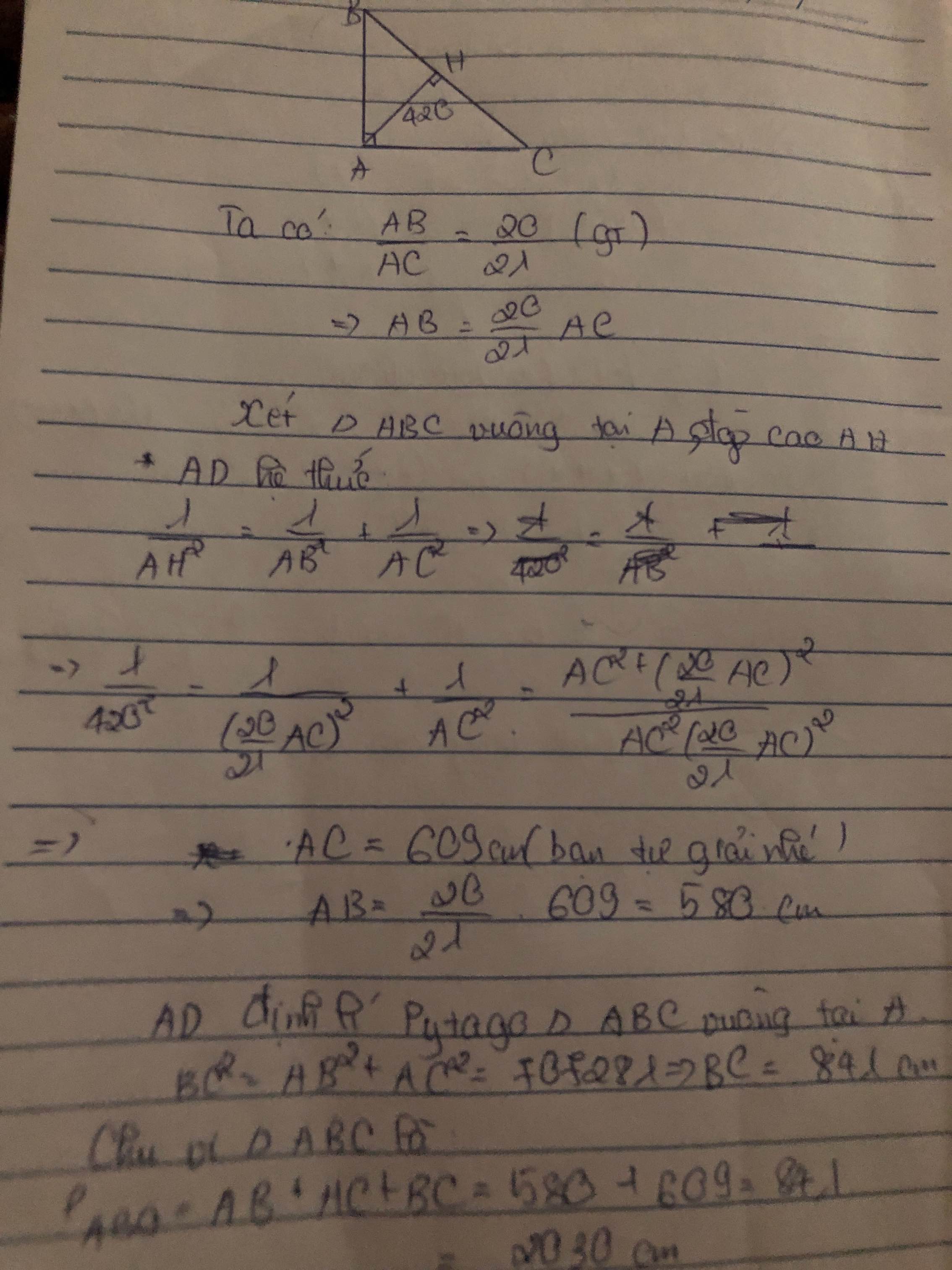\(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)

Áp dụng hệ thức lượng:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{841}{400AC^2}\)

\(\Rightarrow AC=609\) \(\Rightarrow AB=\dfrac{20}{21}AC=580\)

\(BC=\sqrt{AB^2+AC^2}=841\)

Chu vị: \(609+580+841=2030\)

Ta có: \(\dfrac{AB}{AC}=\dfrac{20}{21}\)

nên \(AB=\dfrac{20}{21}\cdot AC\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\dfrac{1}{\dfrac{400}{441}AC^2}+\dfrac{\dfrac{400}{441}}{\dfrac{400}{441}AC^2}=\dfrac{1}{176400}\)

\(\Leftrightarrow\dfrac{400}{441}AC^2=336400\)

\(\Leftrightarrow AC^2=370881\)

hay AC=609(cm)

\(\Leftrightarrow AB=\dfrac{20}{21}\cdot AC=\dfrac{20}{21}\cdot609=580\left(cm\right)\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=580^2+609^2=371461\)

hay BC=841(cm)

Chu vi tam giác ABC là:

AB+AC+BC=580+609+841=2030(cm)

Giải: 

Ta có: AB:AC = 20 : 21 

=> AB:20 = AC:21 (1)

Đặt tỉ số (1) = X,ta có : AB =20X ; AC=21X

Áp dụng định lí PY-TA-GO,ta có:

BC=√(AB²+AC²)=√(20X)²+(21X)²=√(400X²+441X²)=√881X²=29X

Áp dụng hệ thức cạnh và đường cao trong tam giác ABC vuông tại A,ta có:

                        AH = (ABxAC):BC =(20X x 21X):29X =(140:3) X

=> 420 = (140:3)X => X = 9 

=> AB = 20 x 9 = 180 (cm)    

=> AC = 21 x 9 = 189 (cm)    

=> BC = 29 x 9 =261 (cm)    

 => P_abc = 180 + 189 + 261= 630 (cm)       

câu trả lời của bn sai rồi

(20x*21x):29x=14.48275862

Ta cm được: \(\Delta\)ABH\(\infty\)\(\Delta\)CAH

\(\Rightarrow\)\(\dfrac{AB}{AC}=\dfrac{AH}{CH}=\dfrac{BH}{AH}\)

\(\Rightarrow CH=\dfrac{AC\cdot AH}{AB}=441\)

\(\Rightarrow BH=\dfrac{AH^2}{CH}=400\)

Áp dụng định lí pitago vào \(\Delta\)AHC vuông tại H có:

\(AC^2=HC^2+AH^2\)

\(\Rightarrow AC=\)609

AB=580

Chu vi \(\Delta ABC\) là:

Pabc=AB+AC+BC=2030

Xét ΔABH và ΔCAH có:

  \(\widehat{AHB}=\widehat{CHA}=90\left(gt\right)\)

  \(\widehat{ABH}=\widehat{CAH}\) (cùng phụ với \(\widehat{BAH}\) )

=>ΔABH=ΔCAH (g.g)

=>\(\frac{AB}{AC}=\frac{AH}{CH}=\frac{BH}{AH}\)

=>\(\frac{20}{21}=\frac{420}{HC}=\frac{BH}{420}\)

=>\(HC=\frac{420\cdot21}{20}=441\)

    \(BH=\frac{420\cdot20}{21}=400\)

=> BC=HC+HB=441+400=841

Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:

\(AB^2=BH\cdot BC=400\cdot841=336400\Rightarrow AB=580\)

\(AC^2=HC\cdot BC=441\cdot841=370881\Rightarrow AC=609\)

Vậy chu vi của ΔABC là: AB+AC+BC=580+609+841=2030

 AB/AC = 20/21 => Đặt  AB/20  = AC / 21 = x

=> AB = 20x ; AC= 21x

Tam giác ABC vuông tại A , theo PY TA GO :

               \(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(20x\right)^2+\left(21x\right)^2}=\sqrt{400x^2+441x^2}=\sqrt{881x^2}=29x\)

Tam giác ABC vuông tại A, theo HTL :

                        AH = \(\frac{AB.AC}{BC}=\frac{20x.21x}{29x}=\frac{140}{3}x\)

=> 420 = 140/3 * x => x = 9

=> AB = 20 . 9 = 180

=> AC = 21.9 = 189

=> BC = 29 . 9 =261

 => Cabc = 180 + 189 + 261= 630        

lm kieu j ko hieu kai deo j het

630 okkkk

tham khảo câu tl nàu nhé !

 BÀI 1:

a)

·         Trong ∆ ABC, có:     AB²= BC.BH

                           Hay BC= =

·         Xét ∆ ABC vuông tại A, có:

    AB²= BH²+AH²

↔AH²= AB² – BH²

↔AH= =4 (cm)

b)

·         Ta có: HC=BC-BH

      àHC= 8.3 - 3= 5.3 (cm)

·         Trong ∆ AHC, có:    

·                                         

Bài 1:

a)  Áp dụng hệ thức lượng ta có:

   \(AB^2=BH.BC\)

\(\Rightarrow\)\(BC=\frac{AB^2}{BH}\)

\(\Rightarrow\)\(BC=\frac{5^2}{3}=\frac{25}{3}\)

Áp dụng Pytago ta có:

     \(AH^2+BH^2=AB^2\)

\(\Rightarrow\)\(AH^2=AB^2-BH^2\)

\(\Rightarrow\)\(AH^2=5^2-3^2=16\)

\(\Rightarrow\)\(AH=4\)

b)  \(HC=BC-BH=\frac{25}{3}-3=\frac{16}{3}\)

Áp dụng hệ thức lượng ta có:

   \(\frac{1}{HE^2}=\frac{1}{AH^2}+\frac{1}{HC^2}\)

\(\Leftrightarrow\)\(\frac{1}{HE^2}=\frac{1}{4^2}+\frac{1}{\left(\frac{16}{3}\right)^2}=\frac{25}{256}\)

\(\Rightarrow\)\(\frac{1}{HE}=\frac{5}{16}\)

\(\Rightarrow\)\(HE=\frac{16}{5}\)

Xét tam giác ABC vuông tại A:

\(BC^2=AB^2+AC^2\left(Pytago\right)\)

\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{20^2+15^2}=25\left(cm\right)\)

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A:

\(AH.BC=AB.AC\)

\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{20.15}{25}=12\left(cm\right)\)

Ta có: \(P_{ABC}=AB+AC+BC=20+15+25=60\left(cm\right)\)

Có AB^2 = BC . BH

AC^2 = BC . CH

AB^2 : AC^2 = (BC . BH ) : ( BC . CH) 

400/ 441 = BH / CH suy ra BH= 400/ 441 . CH

mà AH² = BH . CH= CH² . 400 /441

240² = CH² . 400/441

suy ra CH= 252

từ đó tính tiếp nhé

Dễ thấy D nằm giữa M và H

Ta có : AD là tia phân giác góc BAC \(\Rightarrow\widehat{PAB}=\widehat{PAC}=\frac{1}{2}\widehat{BAC}=45^o\)

Mà \(\widehat{BAP}=\frac{1}{2}sđ\widebat{BP}=45^o\); \(\widehat{PAC}=\frac{1}{2}sđ\widebat{PC}=45^o\)

\(\Rightarrow sđ\widebat{BP}=sđ\widebat{PC}=90^o\)

Ta có : AM là đường trung tuyến nên M là tâm đường tròn ngoại tiếp tam giác ABC

\(\Rightarrow\widehat{BMP}=sđ\widebat{BP}=90^o\)

\(\Rightarrow BM\perp MP\)hay \(BC\perp MP\)( 1 )

Mà AH là đường cao tam giác ABC nên \(BC\perp AH\) ( 2 )

Từ ( 1 ) và ( 2 ) suy ra AH // MP