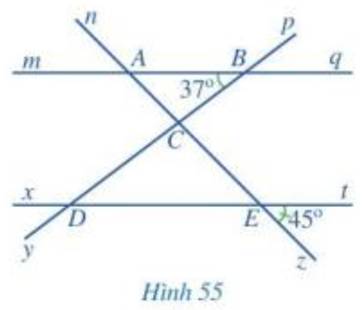
cho hình vẽ
a)kể tên các cặp góc đồng vị bằng nhau b) Tính BAC;CDE c)qua điểm c kề đường thẳng song song hai đường thẳng mq và ct. Tính BCE
Những câu hỏi liên quan
Thay 37 độ bằng 39 độ nha.
Đề bài:
a, Kể tên các góc đồng vị bằng nhau
b, Kể tên các góc so le trong bằng nhau
c, Tính góc BAC,CDE
d, Tính góc BCE(gợi ý từ kẻ đường thẳng ab song song vs mq) Các bn lm hình giúp mik ạ!!!
a, Các góc đồng vị bằng nhau là:
\(\widehat{nAm}\) = \(\widehat{AEx}\); \(\widehat{mAE}\) = \(\widehat{zED}\); \(\widehat{nAB}\) = \(\widehat{AEt}\)
\(\widehat{qAE}\) = \(\widehat{tEz}\); \(\widehat{pBq}\) = \(\widehat{BDE}\); \(\widehat{qBC}\) = \(\widehat{EDy}\); \(\widehat{pBA}\) = \(\widehat{BDx}\); \(\widehat{ABD}\)=\(\widehat{xDy}\)
b, Các góc so le trong:
\(\widehat{ABC}\) = \(\widehat{CDE}\); \(\widehat{mAC}\) = \(\widehat{CEt}\); \(\widehat{BAC}\) = \(\widehat{CED}\); \(\widehat{qBc}\) = \(\widehat{CDx}\)
c, \(\widehat{BAC}\) = \(\widehat{zEt}\) = 450
\(\widehat{CDE}\) = \(\widehat{ABC}\) = 390
d, \(\widehat{BCE}\) = \(\widehat{CDE}\) + \(\widehat{CED}\) (góc ngoài tam giác bằng tổng hai góc trong không kề với nó.
\(\widehat{CED}\) = \(\widehat{zEt}\) = 450 (hai góc đối đỉnh)
\(\widehat{BCE}\) = 390 + 450 = 840
Đúng 4
Bình luận (0)
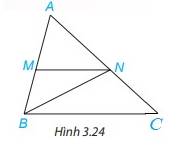
Quan sát hình 3.24.
a) Tìm một góc ở vị trí so le trong với góc MNB.
b) Tìm một góc ở vị trí đồng vị với góc ACB.
c) Kể tên một cặp góc trong cùng phía.
d) Biết MN//BC, em hãy kể tên ba cặp góc bằng nhau trong hình vẽ
a) Góc MNB so le trong với góc NBC
b) Góc ACB đồng vị với góc ANM
c) Các cặp góc trong cùng phía là: góc MNC và góc NCB; góc NMB và góc MBC
d) Vì MN//BC nên
\(\widehat {ANM} = \widehat {ACB}\) (2 góc đồng vị)
\(\widehat {AMN} = \widehat {ABC}\) (2 góc đồng vị)
\(\widehat {MNB} = \widehat {NBC}\) ( 2 góc so le trong)
Đúng 0
Bình luận (0)
Bai 2:Cho các hình vẽ dưới đây aFbEc43211234600120oa) Kể tên các cặp góc so le trong, đồng vị, trong cung phía.b) Tính F_1;F_2;F_3;F_4 c) Hai đường thẳng a, b có song song với nhau không? Vì sao? ( nếu có giải thích bằng 2 cách)
Đọc tiếp
Bai 2:Cho các hình vẽ dưới đây
a) Kể tên các cặp góc so le trong, đồng vị, trong cung phía.
b) Tính \(F_1;F_2;F_3;F_4\)
c) Hai đường thẳng a, b có song song với nhau không? Vì sao? ( nếu có giải thích bằng 2 cách)
\(a,\)So le trong: \(E_1 và F_2;E_2 và F_1\)
Đồng vị: \(E_1 và F_4;E_2 và F_3;E_3 và F_2;E_4 và F_1\)
Trong cùng phía: \(E_1 và F_1;E_2 và F_2\)
\(b,\widehat{F_1}=\widehat{F_3}=120^0\left(đối.đỉnh\right)\\ \widehat{F_2}+\widehat{F_3}=180^0\left(kề.bù\right)\Rightarrow\widehat{F_2}=180^0-120^0=60^0\\ \widehat{F_2}=\widehat{F_4}-60^0\left(đối.đỉnh\right)\)
\(c,C_1:\widehat{F_2}=\widehat{E_3}\left(=60^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(a//b\)
\(C_2:\)\(\widehat{E_1}=\widehat{E_3}=60^0\left(đối.đỉnh\right)\Rightarrow\widehat{E_1}=\widehat{F_2}\left(=60^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(a//b\)
Đúng 2
Bình luận (0)
a. Các cặp góc:
- So le trong là: \(\widehat{E_1}\) và \(\widehat{F_2};\widehat{E_2}\) và \(\widehat{F_1}\)
- Đồng vị là: \(\widehat{E_4},\widehat{F_1};\widehat{E_3},\widehat{F_2};\widehat{E_2},\widehat{F_3};\widehat{E_1},\widehat{F_4}\)
- Trong cùng phía là: \(\widehat{E_1},\widehat{F_1};\widehat{E_2},\widehat{F_2}\)
b. Ta có: \(\widehat{F_1}=\widehat{F_3}=120^o\) (đối đỉnh)
\(\widehat{F_2}=180^o-\widehat{F_1}=180^o-120^o=60^o\)
\(\widehat{F_3}=120^o\)
\(\widehat{F_4}=\widehat{F_2}=60^o\) (đối đỉnh)
c.
C1: Ta có: \(\widehat{E_1}=\widehat{E_3}=60^o\) (đối đỉnh)
Ta thấy: \(\widehat{E_1}=\widehat{F_2}=60^o\)
=> a//b (so le trong)
C2: Ta có: \(\widehat{E_2}=180^o-\widehat{E_3}=180^o-60^o=120^o\)
Ta thấy: \(\widehat{E_2}=\widehat{F_1}=120^o\)
=> a//b (so le trong)
Đúng 0
Bình luận (0)
a) Trong cùng phía:
-E1 và F2
-E2 và F4
Đồng vị:
- E1 và F4
- E2 và F3
- E4 và F1
- E3 và F2
Trong cùng phía:
- E1 và F1
E2 và F2
b) Vì E3 và F2 là hai góc đồng vị
-> E3 = F2 = 60O
Vì F1 và F2 là hai góc kề bù
-> F1 + F2 = 180o
Thay số: F1 + 60O = 180O
-> F1 = 180O – 60O = 120O
Vì F3 và F4 là hai góc kề bù
-> F3 + F4 = 180O
Thay số: 120o + F4 = 180O
-> F4 = 180O – 120O = 60O
c) Vì E3 và F3 là hai góc ngoài cùng phía
-> a//b
Vậy a//b
Đúng 0
Bình luận (2)
Cho hình vẽ bêna) Kể tên các cặp góc so le trong,các cặp góc đồng vị và các cặp góc trong cùng phíab) Tính các góc còn lạibiết aBO 140°, BOn 40°
Đọc tiếp
Cho hình vẽ bên
a) Kể tên các cặp góc so le trong,
các cặp góc đồng vị và các cặp góc
trong cùng phía
b) Tính các góc còn lại
biết aBO = 140°, BOn = 40°
GIÚP MÌNH VỚI MN ƠIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
Đúng 0
Bình luận (1)
a) Bạn tự lm
b) Ta có: \(\widehat{aBo}=\widehat{nOd}=140^0\) (đồng vị)
\(\widehat{nOm}=\widehat{aBc}=40^0\)(đồng vị)
Ta lại có: \(\widehat{aBo}=\widehat{bOm}=140^0\) (so le trong)
\(\widehat{nOB}=\widehat{bBO}=40^0\) (so le trong)
Lại có: \(\widehat{aBO}=\widehat{bBc}=140^0\)(2 góc đối đỉnh)
\(\widehat{nOB}=\widehat{dOm}=40^0\) (2 góc đối đỉnh)
Đúng 0
Bình luận (0)
Cho hình vẽ bêna) Kể tên các cặp góc so le trong,các cặp góc đồng vị và các cặp góc trong cùng phíab) Tính các góc còn lạibiết aBO 140°, BOn 40°
Đọc tiếp
Cho hình vẽ bên
a) Kể tên các cặp góc so le trong,
các cặp góc đồng vị và các cặp góc
trong cùng phía
b) Tính các góc còn lại
biết aBO = 140°, BOn = 40°
![]()
![]()
![]()
![]()
Cho hình vẽ bêna) Kể tên các cặp góc so le trong,các cặp góc đồng vị và các cặp góc trong cùng phíab) Tính các góc còn lạibiết aBO 140°, BOn 40°
Đọc tiếp
Cho hình vẽ bên
a) Kể tên các cặp góc so le trong,
các cặp góc đồng vị và các cặp góc
trong cùng phía
b) Tính các góc còn lại
biết aBO = 140°, BOn = 40°
Bài 1- Cho hình vẽ bên
1 2 3 4 s p 1 2 4 3 m n r
a) Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía.
b) Tính số đo các cặp góc còn lại, biết:
R4 S2 120° .
Đọc tiếp
Bài 1- Cho hình vẽ bên
a) Kể tên các cặp góc so le trong, các cặp góc đồng vị và các cặp góc trong cùng phía.
b) Tính số đo các cặp góc còn lại, biết:
R4 = S2 = 120° .
a) Các cặp góc sole trong là : S3 và R2 ; S4 và R1
Các cặp góc đồng vị là : S1 và R1; S2 và R2; S3 và R4; S4 và R3
Các góc trong cùng phía là : S3 và R1; S4 và R2
b) R4 = S3 = 120\(\)o (2 góc đồng vị)
R4 = R2 = 120o (2 góc đối đỉnh)
R2 + R1 = 180o (2 góc kề bù)
⇒ 120o + R1 =180o
⇒ R1 = 180o - 120o
⇒ R1 = 60o
R1 = S1 = 60o (2 góc đồng vị)
R1 = R3 = 60o (2 góc đối đỉnh)
S1 = S4 = 60o (2 góc đối đỉnh)
Đúng 1
Bình luận (0)
trên tia Ox, lấy 2 điểm A và B sao cho OA= 5cm, OB= 8cm a) tính độ dài đoạn thẳng AB b) kể tên 1 cặp tia đối nhau gốc A 1 cặp tia trùng nhau gốc A c0 vẽ tia At sao cho góc xAt bằng 60 độ. kể tên các góc đỉnh A có trên hình d) mỗi góc đỉnh A kể tên đâu là loại góc nhọn, góc vuông, góc tù hay góc bẹt? Hộ mik với ạ mai mik thi rồi
a: OA<OB
=>A nằm giữa O và B
=>OA+AB=OB
=>AB=8-5=3cm
b: Đối nhau gốc A: AO và Ax
Trùng nhau gốc A: AB và Ax
c: góc xAt, góc tAO
d: Góc nhọn: góc xAt
góc tù: góc tAO
Góc bẹt: góc xAO
Đúng 0
Bình luận (0)
bài 1: Vẽ 4 đường thẳng aa' ,bb' ,cc' ,dd' cắt nhau tại điểm A.
a) Kể tên cặp góc bằng nhau.
b) Cho góc aAb^ = 30' ; góc bAc^ = 40' ; góc aAd^ = 50'. Tính các góc còn lại
CẢM ƠN !




















