\(a,\)So le trong: \(E_1 và F_2;E_2 và F_1\)
Đồng vị: \(E_1 và F_4;E_2 và F_3;E_3 và F_2;E_4 và F_1\)
Trong cùng phía: \(E_1 và F_1;E_2 và F_2\)
\(b,\widehat{F_1}=\widehat{F_3}=120^0\left(đối.đỉnh\right)\\ \widehat{F_2}+\widehat{F_3}=180^0\left(kề.bù\right)\Rightarrow\widehat{F_2}=180^0-120^0=60^0\\ \widehat{F_2}=\widehat{F_4}-60^0\left(đối.đỉnh\right)\)
\(c,C_1:\widehat{F_2}=\widehat{E_3}\left(=60^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(a//b\)
\(C_2:\)\(\widehat{E_1}=\widehat{E_3}=60^0\left(đối.đỉnh\right)\Rightarrow\widehat{E_1}=\widehat{F_2}\left(=60^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(a//b\)
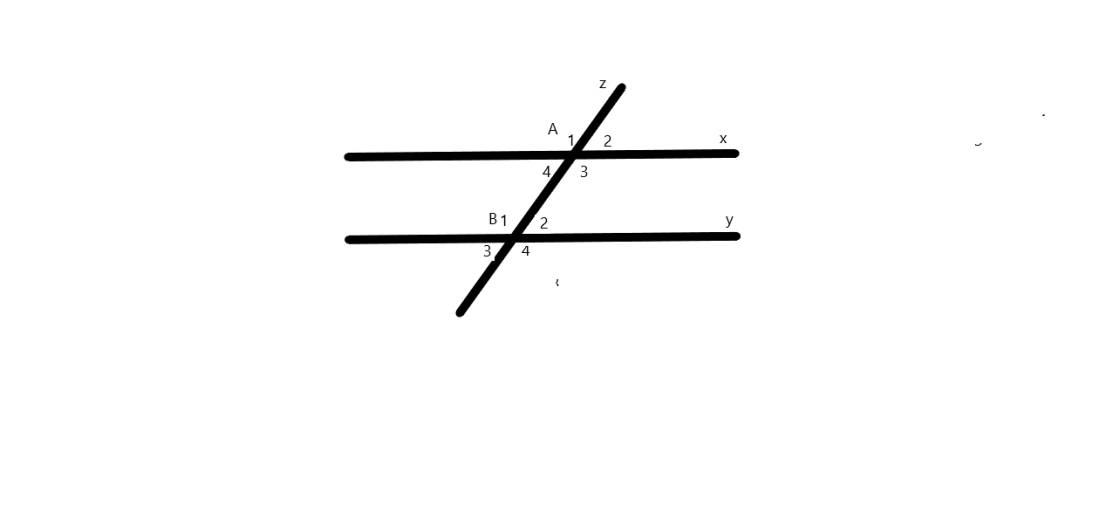
a. Các cặp góc:
- So le trong là: \(\widehat{E_1}\) và \(\widehat{F_2};\widehat{E_2}\) và \(\widehat{F_1}\)
- Đồng vị là: \(\widehat{E_4},\widehat{F_1};\widehat{E_3},\widehat{F_2};\widehat{E_2},\widehat{F_3};\widehat{E_1},\widehat{F_4}\)
- Trong cùng phía là: \(\widehat{E_1},\widehat{F_1};\widehat{E_2},\widehat{F_2}\)
b. Ta có: \(\widehat{F_1}=\widehat{F_3}=120^o\) (đối đỉnh)
\(\widehat{F_2}=180^o-\widehat{F_1}=180^o-120^o=60^o\)
\(\widehat{F_3}=120^o\)
\(\widehat{F_4}=\widehat{F_2}=60^o\) (đối đỉnh)
c.
C1: Ta có: \(\widehat{E_1}=\widehat{E_3}=60^o\) (đối đỉnh)
Ta thấy: \(\widehat{E_1}=\widehat{F_2}=60^o\)
=> a//b (so le trong)
C2: Ta có: \(\widehat{E_2}=180^o-\widehat{E_3}=180^o-60^o=120^o\)
Ta thấy: \(\widehat{E_2}=\widehat{F_1}=120^o\)
=> a//b (so le trong)
a) Trong cùng phía:
-E1 và F2
-E2 và F4
Đồng vị:
- E1 và F4
- E2 và F3
- E4 và F1
- E3 và F2
Trong cùng phía:
- E1 và F1
E2 và F2
b) Vì E3 và F2 là hai góc đồng vị
-> E3 = F2 = 60O
Vì F1 và F2 là hai góc kề bù
-> F1 + F2 = 180o
Thay số: F1 + 60O = 180O
-> F1 = 180O – 60O = 120O
Vì F3 và F4 là hai góc kề bù
-> F3 + F4 = 180O
Thay số: 120o + F4 = 180O
-> F4 = 180O – 120O = 60O
c) Vì E3 và F3 là hai góc ngoài cùng phía
-> a//b
Vậy a//b









 a) k
a) k






