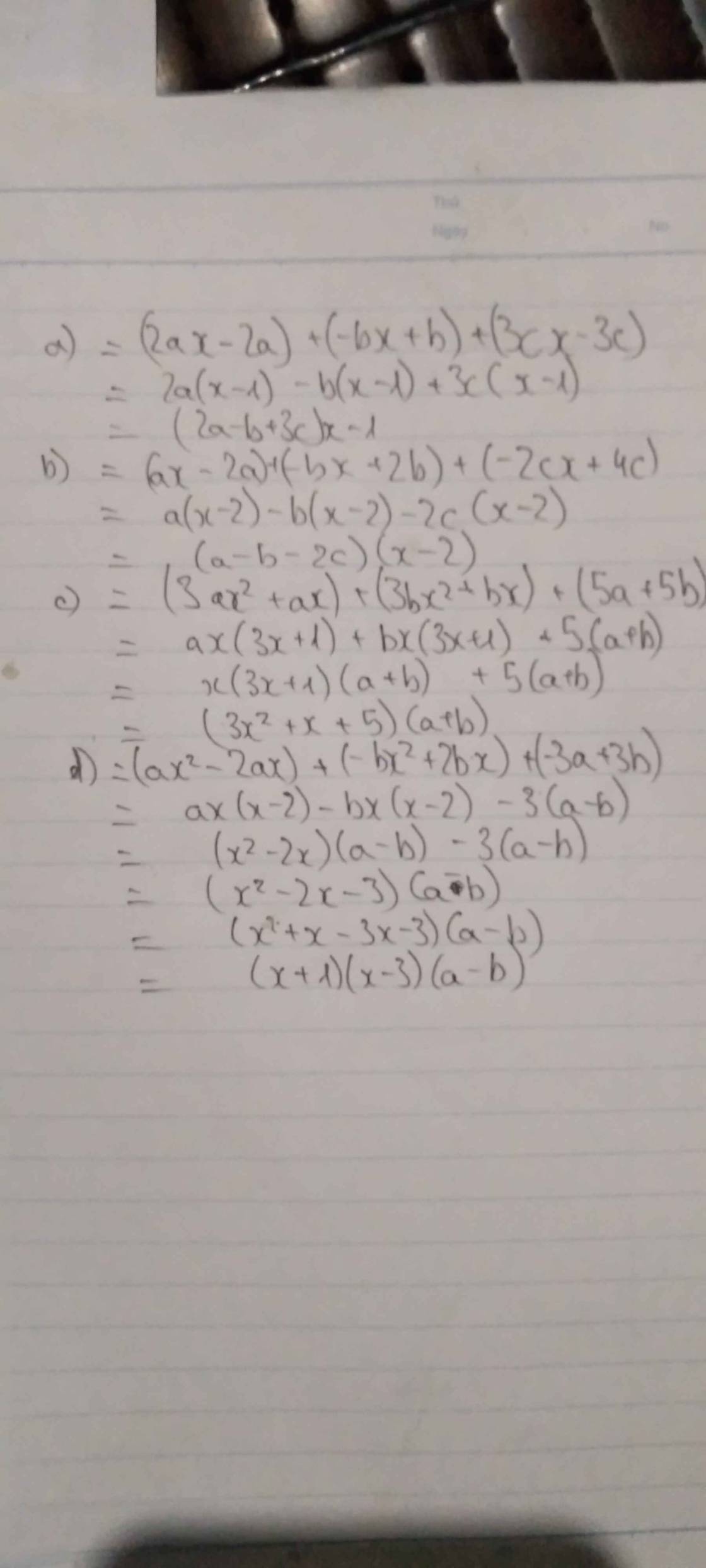sos phân tích thành nhân tử :3ax^2++3bx^2+ã+bx+5a+5b

Những câu hỏi liên quan
Phân tích thành nhân tử (mọi người làm chi tiết ạ)
\(2ax-bx+3cx-2a+b-3c\)
\(ax-bx-2cx-2a+2b+4c\)
\(3ax^2 +3bx^2 +ax+bx+5a+5b\)
\(ax^2 -bx^2 -2ax+2bx-3a+3b\)
\(2ax-bx+3cx-2a+b-3c\\ =x\left(2a-b+3c\right)-\left(2a-b+3c\right)\\ =\left(x-1\right)\left(2a-b+3c\right)\)
\(ax-bx-2cx-2a+2b+4c\\ =x\left(a-b-2c\right)-2\left(a-b-2c\right)\\ =\left(x-2\right)\left(a-b-2c\right)\)
\(3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\)
\(ax^2-bx^2-2ax+2bx-3a+3b\\ =x^2\left(a-b\right)-2x\left(a-b\right)-3\left(a+b\right)\\ =\left(x^2-2x-3\right)\left(a+b\right)\\ =\left(x+1\right)\left(x-3\right)\left(a+b\right)\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử:
a)A=4acx+4bcx+4x+4bx
b)B=ax-bx+cx-3a+3b-3c
c)C=2ax-bx+3cx-2a+b-3c
d)D=ax-bx-2cx-2a+2b+4c
e)E=3ax2+3bx2+ax+bx+5a+5b
f)F=ax2-bx2-2ax+2bx-3a+3b
A = 4acx + 4bcx + 4ax + 4bx ( đã sửa '-' )
= 4x( ac + bc + a + b )
= 4x[ c( a + b ) + ( a + b ) ]
= 4x( a + b )( c + 1 )
B = ax - bx + cx - 3a + 3b - 3c
= x( a - b + c ) - 3( a - b + c )
= ( a - b + c )( x - 3 )
C = 2ax - bx + 3cx - 2a + b - 3c
= x( 2a - b + 3c ) - ( 2a - b + 3c )
= ( 2a - b + 3c )( x - 1 )
D = ax - bx - 2cx - 2a + 2b + 4c
= x( a - b - 2c ) - 2( a - b - 2c )
= ( a - b - 2c )( x - 2 )
E = 3ax2 + 3bx2 + ax + bx + 5a + 5b
= 3x2( a + b ) + x( a + b ) + 5( a + b )
= ( a + b )( 3x2 + x + 5 )
F = ax2 - bx2 - 2ax + 2bx - 3a + 3b
= x2( a - b ) - 2x( a - b ) - 3( a - b )
= ( a - b )( x2 - 2x - 3 )
= ( a - b )( x2 + x - 3x - 3 )
= ( a - b )[ x( x + 1 ) - 3( x + 1 ) ]
= ( a - b )( x + 1 )( x - 3 )
phân tích đa thức thành nhân tử:
ax2-5x2-ax+5x+a-5
3ax2+3bx2+ax+by+5a+5b
ax2-5x2-ax+5x+a-5
=x^2(a-5)-x(a-5)+(a-5)
=(a-5)(x^2-x+1)
cậu ghi sai đề rồi phải là
3ax2+3bx2+ax+bx+5a+5b
=3x^2(a+b)+x(a+b)+5(a+b)
=(a+b)(3x^2+x+5)
Đúng 0
Bình luận (0)
1) \(3ax^2+3bx^2+ax+bx+5a+5b\)
2) \(ax-bx-2cx-2a+2b+4c\)
\(1,3ax^2+3bx^2+ax+bx+5a+5b\)
\(=3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)=\left(a+b\right)\left(3x^2+x+5\right)\)
\(2,ax-bx-2cx-2a+2b+4c=x\left(a-b-2c\right)-2\left(a-b-2c\right)=\left(x-2\right)\left(a-b-2c\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
a^2 + b^2 - 5b -2ab + 5a
a2+b2-5b-2ab+5a
= (b2-2ab+a2)-5(b-a)
= (b-a)2-5(b-a)
= (b-a)(b-a-5)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử :
a, 4(2 - x )^2 + xy - 2y
b, 3a^2x - 3a^2y + abx - aby
c, x( x-y)^3 - y(y-x)^2 - y^2(x-y)
d, 2ax^3 + 6ax^2 + 6ax + 18a
e, x^2y - xy^2 - 3x + 3y
f, 3ax^2 + 3bx^2 + bx + 5a + 5b
Giúp mk vs ạ mk đang cần gấp
a) Ta có: \(4\left(2-x\right)^2+xy-2y\)
\(=4\left(x-2\right)^2+y\left(x-2\right)\)
\(=\left(x-2\right)\left[4\left(x-2\right)+y\right]\)
\(=\left(x-2\right)\left(4x-8+y\right)\)
b) Ta có: \(3a^2x-3a^2y+abx-aby\)
\(=3a^2\left(x-y\right)+ab\left(x-y\right)\)
\(=\left(x-y\right)\left(3a^2+ab\right)\)
\(=a\left(x-y\right)\left(3a+b\right)\)
c) Ta có: \(x\left(x-y\right)^3-y\left(y-x\right)^2-y^2\left(x-y\right)\)
\(=x\left(x-y\right)^3-y\left(x-y\right)^2-y^2\left(x-y\right)\)
\(=\left(x-y\right)\left[x\left(x-y\right)^2-y\left(x-y\right)-y^2\right]\)
\(=\left(x-y\right)\left[x\left(x^2-2xy+y^2\right)-yx+y^2-y^2\right]\)
\(=\left(x-y\right)\left(x^3-2x^2y+xy^2-xy\right)\)
d) Ta có: \(2ax^3+6ax^2+6ax+18a\)
\(=2ax^2\left(x+3\right)+6a\left(x+3\right)\)
\(=\left(x+3\right)\left(2ax^3+6a\right)\)
\(=2a\left(x+3\right)\left(x^3+3\right)\)
e) Ta có: \(x^2y-xy^2-3x+3y\)
\(=xy\left(x-y\right)-3\left(x-y\right)\)
\(=\left(x-y\right)\left(xy-3\right)\)
Đúng 0
Bình luận (0)
Bài 1: phân tích đa thức thành nhân tử
a) 3a^x-3a^2y +abx-aby
b)2ax^3+6ax^2+6ax+18a
c)3ax^2+3bx^2+bx+5a+5b
d)2ax^2-bx^2-2ax+bx+4a-b
Bài 2 tính gt biểu thức
a)x(x-3)-y(3-x)với x =1/3;y=8/3
b)2x^2.(x^2+y^2)+2y^2.(x^2 + y^2)+5.(y^2+x^2) với x^2+y^2=1
Bài 2:
a) x(x - 3)- y(3 - x)
= x(x - 3) + y(x - 3)
= (x - 3)(x + y) (1)
Thay x = \(\frac{1}{3}\); y = \(\frac{8}{3}\)vào (1)
Ta có: (\(\frac{1}{3}\)- 3)(\(\frac{1}{3}\)+ \(\frac{8}{3}\))
= \(\frac{-8}{3}\). 3
= -8
Đúng 0
Bình luận (0)
\(5a^2-5b^2-20a+20 \)
phân tích đa thức thành nhân tử
\(5a^2-5b^2-20a+20b\)
\(=5\left(a^2-b^2\right)-20\left(a-b\right)\)
\(=5\left(a-b\right)\left(a+b\right)-20\left(a-b\right)\)
\(=\left[5\left(a+b\right)-20\right]\left(a-b\right)\)
\(=\left(5a+5b-20\right)\left(a-b\right)\)
Đúng 0
Bình luận (0)
\(5a^2-5b^2-20a+20=-5.\left(b-a+2\right).\left(b+a-2\right)\)
Đúng 0
Bình luận (0)
1, 6a^2y-3aby+4a^2x-2abx2, 5x^2y-5xy^2-a^2x+a^2y3, 2x^2-6xy+5x-15y4, ax^2-5by-5a^2y+2bx5, 2ax^3+6ax^2+6ax+18a6, ax^2-bx^2y-ã+bx+2a-2b7,3ax^2+3bx^2+ã+bx+5a5b8, ax^2-bx^2-2ax+2bx-3a+3b9, 2ax^2-bx^2-2ax+bx-3a+3b10, 2ax^2-5x^2-ax+bx+4a-2b11,ax^2-5x^2-ax+5x+a-5
Đọc tiếp
1, 6a^2y-3aby+4a^2x-2abx
2, 5x^2y-5xy^2-a^2x+a^2y
3, 2x^2-6xy+5x-15y
4, ax^2-5by-5a^2y+2bx
5, 2ax^3+6ax^2+6ax+18a
6, ax^2-bx^2y-ã+bx+2a-2b
7,3ax^2+3bx^2+ã+bx+5a=5b
8, ax^2-bx^2-2ax+2bx-3a+3b
9, 2ax^2-bx^2-2ax+bx-3a+3b
10, 2ax^2-5x^2-ax+bx+4a-2b
11,ax^2-5x^2-ax+5x+a-5