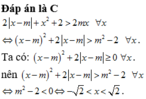Với giá trị nào của m thì bất phương trình: (m−2)x2+2mx−2−m0(�-2)�2+2��-2-�0 có nghiệm
Đọc tiếp
Với giá trị nào của m thì bất phương trình: có nghiệm
Những câu hỏi liên quan
Tìm tất cả các giá trị của m để bất phương trình
2
|
x
-
m
|
+
x
2
+
2
2
m
x
thỏa mãn với mọi x A.
m
-
2
B. không tồn tại m C.
-
2
m
2
D.
m
2
Đọc tiếp
Tìm tất cả các giá trị của m để bất phương trình 2 | x - m | + x 2 + 2 > 2 m x thỏa mãn với mọi x
A. m > - 2
B. không tồn tại m
C. - 2 < m < 2
D. m < 2
Tìm các giá trị của tham số m để các bất phương trình sau nghiệm đúng với mọi x
m ( m + 2 ) x 2 + 2 m x + 2 > 0
+ Nếu m = 0 thì bất phương trình nghiệm đúng với mọi x;
+ Nếu m = -2 thì bất phương tình trở thành – 4x + 2 > 0, không nghiệm đúng với mọi x.
+ Nếu m ≠ 0 và m ≠ -2 thì bất phương trình nghiệm đúng với mọi x khi và chỉ khi
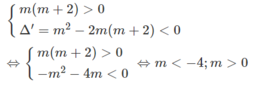
Đáp số: m < -4; m ≥ 0
Đúng 0
Bình luận (0)
Cho phương trình x2 - 2mx - 2 = 0 (1), (m là tham số). Chứng minh phương trình (1) luôn có hai nghiệm x1,x2. Với các giá trị nào của tham số m thì x12 + x22 = 12.
a*c<0
=>Phương trình luôn có hai nghiệm
x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m)^2-2*(-2)=12
=>4m^2+4=12
=>m^2+1=3
=>m^2=2
=>\(m=\pm\sqrt{2}\)
Đúng 1
Bình luận (0)
Cho phương trình x2 - 2mx - 2 = 0 (1), (m là tham số). Chứng minh phương trình (1) luôn có hai nghiệm x1,x2. Với các giá trị nào của tham số m thì x12 + x22 = 12.
\(ac=-2< 0\Rightarrow\) phương trình đã cho luôn có 2 nghiệm (trái dấu)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-2\end{matrix}\right.\)
\(x_1^2+x_2^2=12\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=12\)
\(\Leftrightarrow4m^2+4=12\)
\(\Rightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
Đúng 2
Bình luận (0)
Cho hệ bất phương trình
m
x
2
-
x
-
5
≤
0
(
1
-
m
)
x...
Đọc tiếp
Cho hệ bất phương trình m x 2 - x - 5 ≤ 0 ( 1 - m ) x 2 + 2 m x + m + 2 ≥ 0 . Các giá trị của x thỏa mãn hệ bất phương trình khi m = 1 là:
A. S = 1 - 2 21 2 ; 1 + 2 21 2
B. S = 1 - 3 21 2 ; 1 + 3 21 2
C. S = 1 - 4 21 2 ; 1 + 4 21 2
D. S = 1 - 21 2 ; 1 + 21 2
Chọn D.
Với m = 1 hệ bất phương trình trở thành:
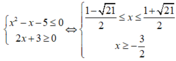
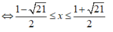
Vậy tập nghiệm hệ bất phương trình là
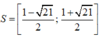
Đúng 0
Bình luận (0)
cho phương trình X^2 - 2mX +m^2 + 1/2 = 0 ( m lafg tham số)
a, với giá trị nào của m thì phương trình có 2 nghiện phân biệt
b, với giá trị nào của m phương trình có 2 nghiệm phân biệt sao cho
M= (X1 - 1)(X2 -`1) đạt GTNN
A=(1 - 1/3) x (1 - 1/4) x ... x (1 - 1/99)
=2/3 x 3/4 x ... x 98/99 (thực hiện phép trừ)
=2 x 1/99 (rút gọn các số giống nhau ở tử và mẫu)
=2/99 (kết quả cuối cùng)
Đúng 0
Bình luận (0)
cho phương trình X^2 - 2mX +m^2 + 1/2 = 0 ( m lafg tham số)
a, với giá trị nào của m thì phương trình có 2 nghiện phân biệt
b, với giá trị nào của m phương trình có 2 nghiệm phân biệt sao cho
M= (X1 - 1)(X2 -`1) đạt GTNN
a/ Phương trình có 2 nghiệm phân biệt khi
\(\Delta'=m^2-m^2-0,5=-0,5< 0\)
Vậy pt này vô nghiệm với mọi m
PS: Xem lại đề đi nhé
Đúng 0
Bình luận (0)
Pt \(\Leftrightarrow\left(x-m\right)^2+\frac{1}{2}\ge\frac{1}{2}\forall x,m\)
Đúng 0
Bình luận (0)
Cho phương trình bậc hai (ẩn x): x 2 - 2mx + 2m – 1 = 0
a) Với giá trị nào của m thì phương trình có nghiệm.
x 2 - 2mx + 2m – 1 = 0
Δ = b 2 - 4ac = 2 m 2 - 4.(2m - 1) = 4 m 2 -8m + 4 = 4 m - 1 2
Do Δ = 4 m - 1 2 ≥ 0 ∀ m nên phương trình luôn có nghiệm với mọi m
Đúng 0
Bình luận (0)
Cho phương trình ( ẩn x ): x2 - 2mx + 1 = 0
a. Tính △'
b. Với giá trị nào của m thì phương trình có nghiệm kép
a) \(\Delta'=m^2-1\)
b) Phương trình có nghiệm kép \(\Leftrightarrow\Delta'=0\Leftrightarrow m^2-1=0\Leftrightarrow m=\pm1\)
Đúng 1
Bình luận (0)