tìm giá trị nn của biểu thức P= căn x + 4/căn x
mọi ng giúp e với e cảm ơn nhiều ạ
cho biểu thức P =căn x+3/ căn x -1 .với các gt nguyên của x tìm gtnn của P
mọi người giúp e với e cảm ơn mn nhìu lắm
e sắp phải nộp rùi ạ
\(P=\sqrt[]{x}+\dfrac{3}{\sqrt[]{x}-1}\left(x>1\right)\)
\(P=\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}+1\)
Áp dụng bất đẳng thức Cauchy cho 2 số \(\sqrt[]{x}-1;\dfrac{3}{\sqrt[]{x}-1}\) ta được :
\(\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}\ge2\sqrt[]{\sqrt[]{x}-1.\dfrac{3}{\sqrt[]{x}-1}}\)
\(\Rightarrow\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}\ge2\sqrt[]{3}\)
\(\Rightarrow P=\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}+1\ge2\sqrt[]{3}+1\)
\(\Rightarrow Min\left(P\right)=2\sqrt[]{3}+1\)
sorry mn cho e sửa lại đề ạ
tìm gtln của p ạ
tìm gtnn của biểu thức p= x+5/căn x+2
giúp e với ạ hiuhiu e nghĩ mãi hong đc chìu nộp r e cảm ơn nhìu
\(P=\dfrac{x+5}{\sqrt[]{x}+2}=\dfrac{x-4+9}{\sqrt[]{x}+2}=\dfrac{\left(\sqrt[]{x}+2\right)\left(\sqrt[]{x}-2\right)+9}{\sqrt[]{x}+2}\)
\(=\left(\sqrt[]{x}-2\right)+\dfrac{9}{\sqrt[]{x}+2}=\left(\sqrt[]{x}+2\right)+\dfrac{9}{\sqrt[]{x}+2}-4\)
Áp dụng bất đẳng thức Cauchy cho 2 số \(\left(\sqrt[]{x}+2\right);\dfrac{9}{\sqrt[]{x}+2}\left(x\ge0\right)\)
\(\left(\sqrt[]{x}+2\right)+\dfrac{9}{\sqrt[]{x}+2}\ge2\sqrt[]{\left(\sqrt[]{x}+2\right).\dfrac{9}{\sqrt[]{x}+2}}=2.3=6\)
\(\Rightarrow P=\left(\sqrt[]{x}+2\right)+\dfrac{9}{\sqrt[]{x}+2}-4\ge6-4=2\)
\(\Rightarrow P\ge2\Rightarrow Min\left(P\right)=2\)
Bạn xem lại đề có phải \(P=x+\dfrac{5}{\sqrt[]{x}+2}\) không?
Tìm giá trị nhỏ nhất của biểu thức D=x - √x +1 với x>0
mọi người giúp e với ạ e cảm ơn rất nhiều ♥
với những giá trị nào của x thì biểu thức B = (2x + 7*( căn bậc hai của x) + 6) / (x+(căn bậc hai của x) -2)
mong thầy cô hãy giúp dùm em sớm ạ, em cảm ơn nhiều !!!!!
Với giá trị nào của x thì căn thức xác định:
Mọi người giúp em với ạ, câu nào cũng được ạ, em cảm ơn nhiều ạ!!!
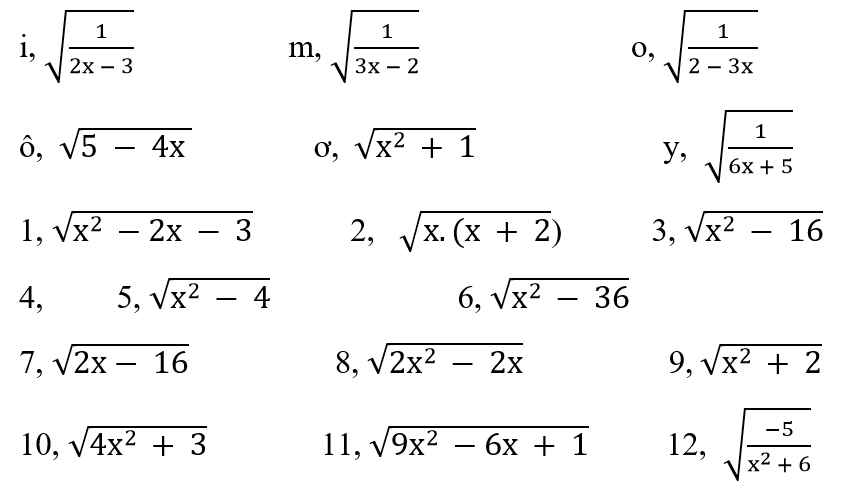
1: ĐKXĐ: (x-3)(x+1)>=0
=>x>=3 hoặc x<=-1
2: ĐKXĐ: x(x+2)>=0
=>x>=0 hoặc x<=-2
3: ĐKXĐ: (x-4)(x+4)>=0
=>x>=4 hoặc x<=-4
4: DKXĐ: (x-2)(x+2)>=0
=>x>=2 hoặc x<=-2
6: ĐKXĐ: (x-6)(x+6)>=0
=>x>=6 hoặc x<=-6
7: ĐKXĐ: 2x-16>=0
=>x>=8
8: ĐKXĐ: x(x-1)>=0
=>x>=1 hoặc x<=0
Mọi người giúp em bài này với ạ . cần gấp lát nữa 5 rưỡi em đi học rồi ạ
bài 1 :Tìm giá trị nhỏ nhất của biểu thức :
a) A= x2 + 4x + 5
b) B= ( x+3 ) ( x-11 ) + 2016
c) C= x2 + 5x + 8
bài 2 : Tìm giá trị lớn nhất của biểu thức :
a) D= 5 - 8x - x2
b) E= x4 + x2 + 2
Mọi người giúp em với :(( em cảm ơn nhiều nhiều lắm ạ
Bài 1:
a) A= x2 + 4x + 5
=x2+4x+4+1
=(x+2)2+1\(\ge\)0+1=1
Dấu = khi x+2=0 <=>x=-2
Vậy Amin=1 khi x=-2
b) B= ( x+3 ) ( x-11 ) + 2016
=x2-8x-33+2016
=x2-8x+16+1967
=(x-4)2+1967\(\ge\)0+1967=1967
Dấu = khi x-4=0 <=>x=4
Vậy Bmin=1967 <=>x=4
Bài 2:
a) D= 5 - 8x - x2
=-(x2+8x-5)
=21-x2+8x+16
=21-x2+4x+4x+16
=21-x(x+4)+4(x+4)
=21-(x+4)(x+4)
=21-(x+4)2\(\le\)0+21=21
Dấu = khi x+4=0 <=>x=-4
b)đề sai à
ài 1:
a) A= x2 + 4x + 5
=x2+4x+4+1
=(x+2)2+1$\ge$≥0+1=1
Dấu = khi x+2=0 <=>x=-2
Vậy Amin=1 khi x=-2
b) B= ( x+3 ) ( x-11 ) + 2016
=x2-8x-33+2016
=x2-8x+16+1967
=(x-4)2+1967$\ge$≥0+1967=1967
Dấu = khi x-4=0 <=>x=4
Vậy Bmin=1967 <=>x=4
Bài 2:
a) D= 5 - 8x - x2
=-(x2+8x-5)
=21-x2+8x+16
=21-x2+4x+4x+16
=21-x(x+4)+4(x+4)
=21-(x+4)(x+4)
=21-(x+4)2$\le$≤0+21=21
Dấu = khi x+4=0 <=>x=-4
b)đề sai à
Rút gọn biểu thức T = căn 27 + 3 / căn 3 Giúp e với e cảm ơn ạ
\(T=\dfrac{\sqrt{27}+3}{\sqrt{3}}=\dfrac{3\sqrt{3}+3}{\sqrt{3}}=\dfrac{3\left(\sqrt{3}+1\right)}{\sqrt{3}}=\sqrt{3}\left(\sqrt{3}+1\right)=3+\sqrt{3}\)
`T=\sqrt{27}+3/\sqrt{3}`
`T=3\sqrt{3}+\sqrt{3}`
`T=4\sqrt{3}`
Tìm giá trị của nhỏ nhất cảu biểu thức: A= |x-1|+|x+3| .Giúp e với ạ em cảm ơn trc
\(A=\left|x-1\right|+\left|x+3\right|=\left|1-x\right|+\left|x+3\right|\)
\(A\ge\left|1-x+x+3\right|=4\)
Vậy giá trị nhỏ nhất của biểu thức A là 4.
Tham khảo thanh này để soạn đề chính xác hơn nha :vvv
a) Ta có: \(M=\left(\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\right)\cdot\dfrac{x+3\sqrt{x}}{7-\sqrt{x}}\)
\(=\left(\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{7-\sqrt{x}}\)
\(=\dfrac{x-9-\left(x-2\sqrt{x}+\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{7-\sqrt{x}}\)
\(=\dfrac{x-9-x+\sqrt{x}+2}{\left(\sqrt{x}-2\right)}\cdot\dfrac{1}{-\left(\sqrt{x}-7\right)}\)
\(=\dfrac{\sqrt{x}-7}{\sqrt{x}-2}\cdot\dfrac{-1}{\sqrt{x}-7}\)
\(=\dfrac{-1}{\sqrt{x}-2}\)(1)
b) Ta có: \(x^2-4x=0\)
\(\Leftrightarrow x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=4\left(loại\right)\end{matrix}\right.\)
Thay x=0 vào biểu thức (1), ta được:
\(M=\dfrac{-1}{\sqrt{0}-2}=\dfrac{-1}{-2}=\dfrac{1}{2}\)
Vậy: Khi \(x^2-4x=0\) thì \(M=\dfrac{1}{2}\)