a: Xét tứ giác AEBC có 

M là trung điểm của AB

M là trung điểm của EC

Do đó: AEBC là hình bình hành

Suy ra: AE=BC

b: Xét tứ giác ABCF có 

N là trung điểm của AC

N là trung điểm của BF

Do đó: ABCF là hình bình hành

Suy ra: AF=BC

mà AE=BC

nên AE=FA

a: Xét tứ giác AEBC có 

M là trung điểm của AB

M là trung điểm của EC

Do đó: AEBC là hình bình hành

Suy ra: AE=BC

b: Xét tứ giác ABCF có 

N là trung điểm của AC

N là trung điểm của BF

Do đó: ABCF là hình bình hành

Suy ra: AF=BC

mà AE=BC

nên AE=FA

a: Xét tứ giác AEBC có 

M là trung điểm của AB

M là trung điểm của EC

Do đó: AEBC là hình bình hành

Suy ra: AE=BC

b: Xét tứ giác ABCF có 

N là trung điểm của AC

N là trung điểm của BF

Do đó: ABCF là hình bình hành

Suy ra: AF=BC

mà AE=BC

nên AE=FA

a: Xét tứ giác ABCD có 

N là trung điểm của AC
N là trung điểm của BD

Do đó: ABCD là hình bình hành

Suy ra: AD=BC

a: Xét tứ giác ADCB có 

N là trung điểm của AC

N là trung điểm của DB

Do đó: ADCB là hình bình hành

Suy ra: DA=BC

xét tam giác ame và tam giác bmc

me=mc (gt)

góc ema= góc bmc (đối đỉnh)

am=bm( m là trung điểm của ab)

=> tam giác ame= tam giác bmc(c.g.c)

=> góc eam= góc cbm ( 2 cạnh tương ứng)

mà góc eam và góc cbm SLT

=>ae //bc

xét tam giác afn và tam giác cbn

fn=bn (gt)

góc an f= góc bnc (đ đ)

an=cn ( n là trung điểm của ac)

=> tam giác a fn= tam giác cbn (c.g.c)

=> a f=cb (2 cạnh t ung)

mà ae=cb (tam giác ame= tam giác bmc)

=>a f= ae (=cb)

=> a là trung điểm của e f

a,b: Xét tứ giác AECB có

N là trung điểm chung của AC,EB

nên AECB là hình bình hành

=>AE//BC và AE=BC

c: Xét tứ giác AFBC có

M là trung điểm chung của AB và FC

nên AFBC là hình bình hành

=>AF//BC

=>F,A,E thẳng hàng

CÍU

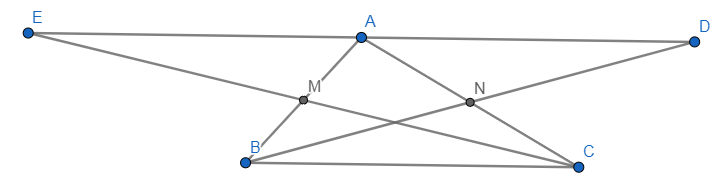
\(a,Xét\) \(\Delta ADN\) \(và\) \(\Delta CBN\) \(có:\) 

\(NC=NA\\ \widehat{BNC}=\widehat{AND}\\ NB=ND\)

\(\Rightarrow\Delta ADN=\Delta CBN\left(c.g.c\right)\)

\(\Rightarrow AD=BC\) (cạnh tương ứng)

\(b,\Rightarrow\widehat{ADN}=\widehat{NBC}\) (góc tương ứng)

\(\Rightarrow AD\) song song với BC (so le trong)

\(CM:\Delta AME=\Delta BMC\) (bạn tự CM nha)

Từ đó suy ra \(EA=BC\) (cạnh tương ứng) mà BC=AD \(\Rightarrow EA=AD\) (1)

\(\Rightarrow\widehat{AEM}=\widehat{MCB}\) (góc tương ứng)

\(\Rightarrow AE\) song song với BC

Mà \(AE\) song song với BC, AD song song với BC\(\Rightarrow E,A,D\) thẳng hàng (2)

Từ (1) và (2) suy ra A là trung điểm của ED

(đpcm)

a, Vì \(\left\{{}\begin{matrix}AN=NC\\\widehat{AND}=\widehat{BNC}\left(đối.đỉnh\right)\\BN=ND\end{matrix}\right.\) nên \(\Delta AND=\Delta CNB\left(c.g.c\right)\)

Do đó \(AD=BC\)

b, Vì \(\left\{{}\begin{matrix}AM=MB\\\widehat{AME}=\widehat{BMC}\left(đối.đỉnh\right)\\EM=MC\end{matrix}\right.\) nên \(\Delta AME=\Delta BMC\left(c.g.c\right)\)

Do đó \(\widehat{MAE}=\widehat{MBC}\) mà 2 góc này ở vị trí so le trong nên AE//BC

c, Vì \(\widehat{NAD}=\widehat{NCB}\left(\Delta AND=\Delta CNB\right)\) mà 2 góc này ở vị trí slt nên AD//BC

Mà AE//BC nên A,D,E thẳng hàng

Ta có \(AE=BC\left(\Delta AME=\Delta BMC\right)\)

Mà \(AD=BC\left(cmt\right)\) nên \(AD=AE\)

Vậy A là trung điểm DE

Xét \(\Delta BNC\)và \(\Delta ANE\)có :

AN=NC(GT)

NE=NB(GT)

GÓC ANE = GÓC BNC (ĐỐI ĐỈNH)

\(\Rightarrow\Delta BNC=\Delta ANE\left(C-G-C\right)\)

=>BC=AE(2 CẠNH TƯƠNG ỨNG )(1)

CHỨNG MINH TƯƠNG TỰ TA CÓ:

FA=CB(2)

TỪ (1) VÀ (2) =>AE=FA (ĐPCM)