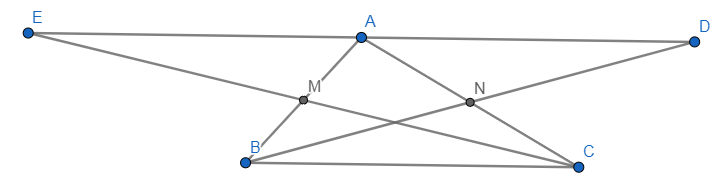
\(a,Xét\) \(\Delta ADN\) \(và\) \(\Delta CBN\) \(có:\)
\(NC=NA\\ \widehat{BNC}=\widehat{AND}\\ NB=ND\)
\(\Rightarrow\Delta ADN=\Delta CBN\left(c.g.c\right)\)
\(\Rightarrow AD=BC\) (cạnh tương ứng)
\(b,\Rightarrow\widehat{ADN}=\widehat{NBC}\) (góc tương ứng)
\(\Rightarrow AD\) song song với BC (so le trong)
\(CM:\Delta AME=\Delta BMC\) (bạn tự CM nha)
Từ đó suy ra \(EA=BC\) (cạnh tương ứng) mà BC=AD \(\Rightarrow EA=AD\) (1)
\(\Rightarrow\widehat{AEM}=\widehat{MCB}\) (góc tương ứng)
\(\Rightarrow AE\) song song với BC
Mà \(AE\) song song với BC, AD song song với BC\(\Rightarrow E,A,D\) thẳng hàng (2)
Từ (1) và (2) suy ra A là trung điểm của ED
(đpcm)











