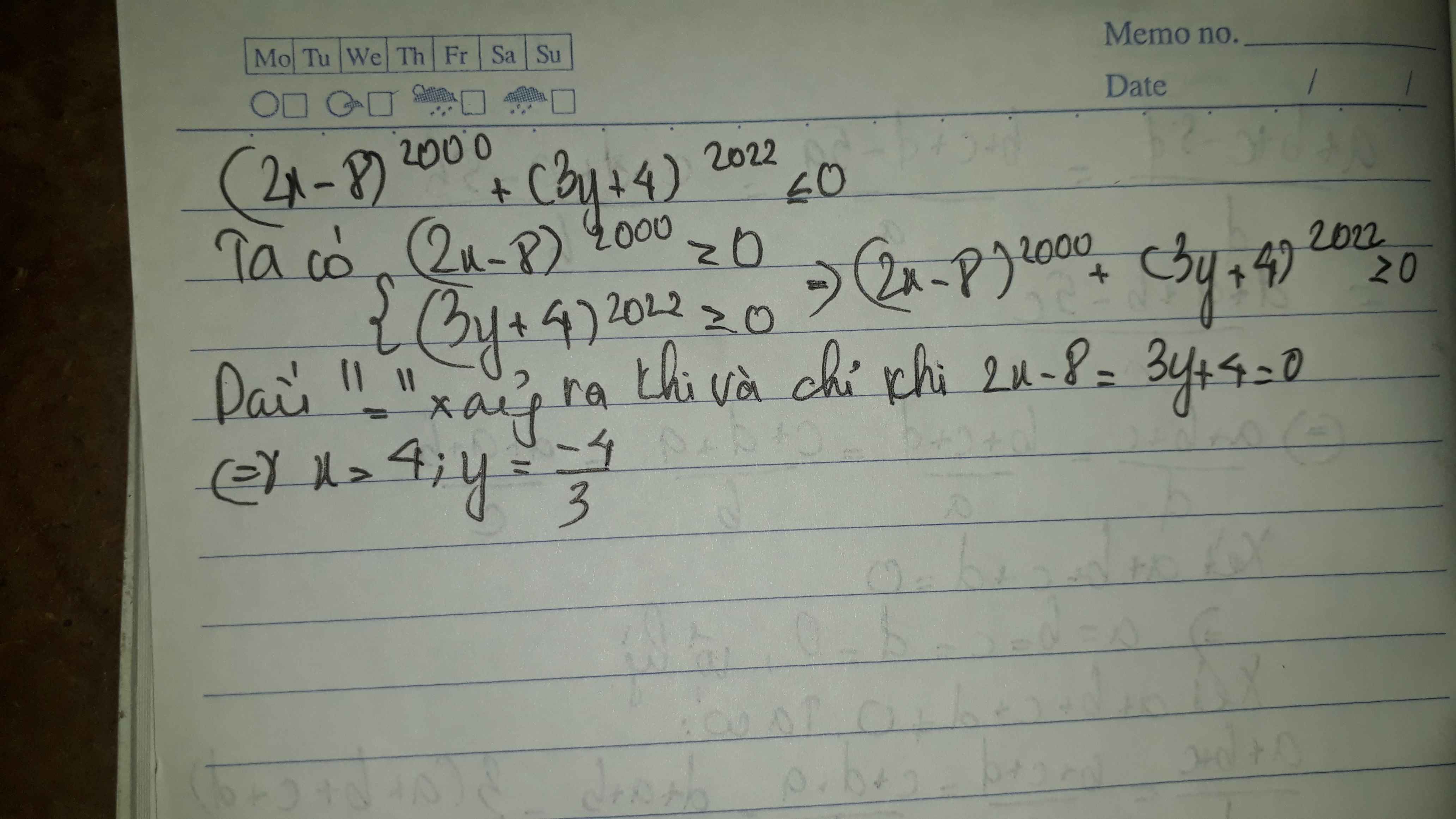Tìm x , y biết: (2x -5)2022 + (3y +4)2024 ≤ 0

Những câu hỏi liên quan
Tìm x,y biết
(2x-5)2023+(3y+4)2024≤0
Em xem lại số mũ của 2x - 5y nhé
2023 hay 2024?
Đúng 0
Bình luận (0)
Tìm x:
a) (2x - 5)2022
b) (3x + 4)2024
Có thể đưa ra lời giải cụ thể ko ạ, 0-0
a,Nghiệm của (2\(x\) - 5)2022 là giá trị của \(x\) thỏa mãn
(2\(x\) - 5)2022 = 0
2\(x\) - 5 = 0
2\(x\) = 5
2\(x\) = 5:2
\(x\) = 2,5
b, Nghiệm của (3\(x\) + 4)2024 là giá trị của \(x\) thỏa mãn:
(3\(x\) + 4)2024 = 0
3\(x\) + 4 = 0
3\(x\) = -4
\(x\) = - 4 : 3
\(x\) = -\(\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
tìm x,y biết ( 2x - 8 ) mũ 2000 + ( 3y + 4 ) mũ 2022 bé hơn hoặc bằng 0
Ta có: \(\left(2x-8\right)^{2000}+\left(3y+4\right)^{2022}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-8=0\\3y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=8\\3y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-\dfrac{4}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm số nguyên dương x sao cho 5x +13 là bội của 2x+1
Tìm x biết (2x-18).(3x+12)=0
Tính S= 1-2-3+4+
5-6-7+8+...+2021-2022-2023+2024+2025
1. Giải:
Do \(5x+13B\in\left(2x+1\right)\Rightarrow5x+13⋮2x+1.\)
\(\Rightarrow2\left(5x+13\right)⋮2x+1\Rightarrow10x+26⋮2x+1.\)
\(\Rightarrow5\left(2x+1\right)+21⋮2x+1.\)
Do 5(2x+1)⋮2x+1⇒ Ta cần 21⋮2x+1.
⇒ 2x+1 ϵ B(21)=\(\left\{1;3;7;21\right\}.\)
Ta có bảng:
| 2x+1 | 1 | 3 | 7 | 21 |
| x | 0 | 1 | 3 | 10 |
| TM | TM | TM | TM |
Vậy xϵ\(\left\{0;1;3;10\right\}.\)
2. Giải:
Do (2x-18).(3x+12)=0.
⇒ 2x-18=0 hoặc 3x+12=0.
⇒ 2x =18 3x =-12.
⇒ x =9 x =-4.
Vậy xϵ\(\left\{-4;9\right\}.\)
3. S= 1-2-3+4+5-6-7+8+...+2021-2022-2023+2024+2025.
S= (1-2-3+4)+(5-6-7+8)+...+(2021-2022-2023+2024)+2025 Có 506 cặp.
S= 0 + 0 + ... + 0 + 2025.
⇒S= 2025.
Đúng 0
Bình luận (0)
Tìm đa thức M biết rằng:M+(5x^2-2xy)=6x^2+9xy-y^2.Tính giá trị của M khi x,y thỏa mãn (2x-5)^2020+(3y+4)^2022 <hoặc=0
M=6x^2+9xy-y^2-5x^2+2xy=x^2+11xy-y^2
(2x-5)^2020+(3y+4)^2022<=0
=>x=5/2 và y=-4/3
M=25/4+11*5/2*(-4/3)-16/9=-1159/36
Đúng 0
Bình luận (0)
(2x + 4) mũ 2024 + I 3y - 9 I mũ 2023 = 0. tìm x và y. nhanh nhé .mk đang cần gấp😊😊
\(\left(2x+4\right)^{2024}+\left(\left|3y-9\right|\right)^{2023}=0\) (*)
Ta có: \(\left(2x+4\right)^{2024}\ge0\forall x\) (vì có số mũ chẵn) (1)
\(\left(\left|3y-9\right|\right)^{2023}\ge0\forall y\) (vì giá trị tuyệt đối luôn ≥0) (2)
Từ (1) và (2) ta có:
\(\Rightarrow\left\{{}\begin{matrix}2x+4=0\\3y-9=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=3\end{matrix}\right.\)
Vậy: ...
Đúng 1
Bình luận (0)
(x-1/3)^2022+ (1/4-y)^2024 =0
=>x-1/3=0 và 1/4-y=0
=>x=1/3 và y=1/4
Đúng 0
Bình luận (0)
(2x-5)^2024 + ( 3y+4)^26 ≤ 0
`(2x-5)^2024 + (3y+4)^26 <= 0`
Vì `(2x-5)^2024 >= 0 AA x`
`(3y+4)^26 >= 0 AA x`
`=>{(2x-5=0),(3y+4=0):}`
`<=>{(x=5/2),(x=-4/3):}`
Đúng 2
Bình luận (0)
Ta thấy: (2x - 5)2024≥ 0 ∀ x ∈ R
(3y + 4)26 ≥ 0 ∀ y ∈ R
=> (2x - 5)2024 + (3y + 4)26 ≥ 0
Mặt khác: (2x - 5)2024 + (3y + 4)26 ≤ 0
Suy ra: (2x - 5)2024 + (3y + 4)26 = 0
\(\Leftrightarrow\left\{{}\begin{matrix}2x-5=0\\3y+4=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy...
Đúng 2
Bình luận (0)
tìm x,y,z biết(2x-1)^2022+(y-2/5)^2022+|x+y-z|=0
\(\left(2x-1\right)^{2020}+\left(y-\frac{2}{5}\right)^{2022}+\left|x+y-z\right|=0\)
Ta có : \(\left(2x-1\right)^{2020}\ge0\forall x;\left(y-\frac{2}{5}\right)^{2022}\ge0\forall x;\left|x+y-z\right|\ge0\forall x;y;z\)
Dấu bằng xảy ra <=> \(x=\frac{1}{2};y=\frac{2}{5};z=x+y=\frac{1}{2}+\frac{2}{5}=\frac{9}{10}\)
Vậy \(x=\frac{1}{2};y=\frac{2}{5};z=\frac{9}{10}\)