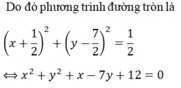Gọi P là trung điểm MN \(\Rightarrow P\left(0;-1\right)\)

\(\overrightarrow{MN}=\left(2;-4\right)=2\left(1;-2\right)\Rightarrow\) trung trực của MN nhận (1;-2) là 1 vtpt

Phương trình trung trực MN:

\(1\left(x-0\right)-2\left(y+1\right)=0\Leftrightarrow x-2y-2=0\)

Gọi I là tâm đường tròn cần tìm \(\Rightarrow\) I là giao điểm của d và trung trực MN

Tọa độ I thỏa mãn: \(\left\{{}\begin{matrix}x-2y-2=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow I\left(-\dfrac{4}{3};-\dfrac{5}{3}\right)\)

\(\overrightarrow{IM}=\left(\dfrac{1}{3};\dfrac{8}{3}\right)\Rightarrow R^2=IM^2=\dfrac{65}{9}\)

Phương trình: \(\left(x+\dfrac{4}{3}\right)^2+\left(y+\dfrac{5}{3}\right)^2=\dfrac{65}{9}\)

Đáp án B

I nằm trên d nên I(x;-2x-5)

IA=IB=R

=>(x-1)^2+(-2x-5+3)^2=(x+3)^2+(-2x-5-1)^2

=>x^2-2x+1+4x^2+8x+4=x^2+6x+9+4x^2+24x+36

=>6x+5=30x+45

=>-24x=40

=>x=-5/3

=>I(-5/3;-5/3)

A(1;-3)

=>R=4/3*căn 5

=>(C): (x+5/3)^2+(y+5/3)^2=80/9

Đáp án B

Gọi I (a; b) là tâm của đường tròn (C)  do đó:

AI² = BI²

Nên ( a-1) ²+ (b-3) ² = (a-3) ²+ (b-1) ²

=> a= b  (1)

 Mà  I( a; b) thuộc d: 2x- y + 7= 0 nên 2a – b+ 7= 0 (2)

Thay (1) vào (2) ta có: a= -7 => b= -7

Khi đó: R²= AI²= 164 .

Vậy  phương trình (C) : ( x+ 7)²+ (y+7)²= 164 .

a) Ta có phương trình đường tròn là \(({C_1}):{\left( {x + 2} \right)^2} + {\left( {y - 4} \right)^2} = 81\)

b) Ta có: \(\overrightarrow {IA}  = (3;3) \Rightarrow IA = 3\sqrt 2  = R\)

Suy ra phương trình đường tròn là; \({C_2}:{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 18\)

c) Vì tâm đường tròn nằm trên đường thẳng \(4x + y - 16 = 0\) nên có tọa độ \(I\left( {a;16 - 4a} \right)\)

Ta có: \(IA = \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {16 - 4a - 1} \right)}^2}} ,IB = \sqrt {{{\left( {a - 6} \right)}^2} + {{\left( {16 - 4a - 5} \right)}^2}} \)

A, B thuộc đường tròn nên \(IA = IB \Rightarrow \sqrt {{{\left( {a - 4} \right)}^2} + {{\left( {16 - 4a - 1} \right)}^2}}  = \sqrt {{{\left( {a - 6} \right)}^2} + {{\left( {16 - 4a - 5} \right)}^2}} \)

\(\begin{array}{l} \Rightarrow {\left( {a - 4} \right)^2} + {\left( {16 - 4a - 1} \right)^2} = {\left( {a - 6} \right)^2} + {\left( {16 - 4a - 5} \right)^2}\\ \Rightarrow {\left( {a - 4} \right)^2} + {\left( {15 - 4a} \right)^2} = {\left( {a - 6} \right)^2} + {\left( {11 - 4a} \right)^2}\\ \Rightarrow  - 28a =  - 84 \Rightarrow a = 3\end{array}\)

Suy ra tâm đường tròn là \(I(3;4)\), bán kính \(R = IA = \sqrt {10} \)

Phương trình đường tròn trên là \(({C_3}):{\left( {x - 3} \right)^2} + {\left( {y - 4} \right)^2} = 10\)

d) Giả sử phương trình đường tròn có dạng \({x^2} + {y^2} - 2mx - 2ny + p = 0\) (với tâm \(I(m;n),R = \sqrt {{m^2} + {n^2} - p} \))

Đường tròn đi qua gốc tọa độ và cắt 2 trục tọa độ tại các điểm có hoành độ a và tung độ là b nên ta có hệ phương trình:

Ta có điều kiện \(a,b \ne 0\), vì khi bằng 0 thì trùng với gốc tọa độ

\(\left\{ \begin{array}{l}{0^2} + {0^2} - 2m.0 - 2n.0 + p = 0\\{a^2} + {0^2} - 2ma - 2n.0 + p = 0\\{0^2} + {b^2} - 2m.0 - 2nb + p = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}p = 0\\{a^2} - 2ma = 0\\{b^2} - 2nb = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}p = 0\\m = \frac{a}{2}\\n = \frac{b}{2}\end{array} \right.\)

Vậy phương trình chính tắc của đường tròn trên là \({x^2} + {y^2} - ax - by = 0\)

Lời giải:

Do $I\in (x-2y-1=0)$ nên gọi tọa độ của $I$ là $(2a+1,a)$

Đường tròn đi qua 2 điểm $A,B$ nên: $IA^2=IB^2=R^2$

$\Leftrightarrow (2a+1+2)^2+(a-1)^2=(2a+1-2)^2+(a-3)^2=R^2$

$\Rightarrow a=0$ và $R^2=10$

Vậy PTĐTr là: $(x-1)^2+y^2=10$

Giả sử \(I=\left(2m+1;m\right)\)

Ta có: \(IA=IB\)

\(\Leftrightarrow\sqrt{\left(-2-2m-1\right)^2+\left(1-m\right)^2}=\sqrt{\left(2-2m-1\right)^2+\left(3-m\right)^2}\)

\(\Leftrightarrow4m^2+9+12m+m^2-2m+1=4m^2-4m+1+m^2-6m+9\)

\(\Leftrightarrow5m^2+10m+10=5m^2-10m+10\)

\(\Leftrightarrow m=0\)

\(\Rightarrow I=\left(1;0\right)\)

Bán kính \(R=\sqrt{\left(2-1\right)^2+3^2}=\sqrt{10}\)

Phương trình đường tròn: \(\left(x-1\right)^2+y^2=10\)

Do tâm nằm trên đường thẳng ∆: x +y – 3 = 0 nên tâm I(x; 3 – x). Mà đường tròn đi qua A(-1; 3), B(1;4) nên 

I A 2 = I B 2 ⇔ x + 1 2 + − x 2 = x − 1 2 + − 1 − x 2

⇔ x 2 + ​ 2 x + ​ 1    + ​ x 2 = x 2 − 2 x + 1 + ​ 1 + ​ 2 x + x 2 ⇔ 2 x 2 + ​ 2 x + ​ 1 = 2 x 2 + ​ 2 ⇔ 2 x = 1 ⇔ x = 1 2

Tọa độ điểm  I 1 2 ;     5 2

Bán kính  I A =    − 1 − 1 2 2 + ​ 3 − 5 2 2 = 10 2

Phương trình đường tròn là  x − 1 2 2 + y − 5 2 2 = 5 2 ⇔   x 2 + y 2 − x − 5 y + 4 = 0

ĐÁP ÁN C

a) Để tìm phương trình đường tròn © có tâm I(2,3) đi qua điểm A(5,7), ta sử dụng công thức khoảng cách từ điểm đến tâm đường tròn:

$I\hat{A} = \sqrt{(x_A - x_I)^2 + (y_A - y_I)^2}$

Với I là tâm đường tròn, A là điểm trên đường tròn.

Ta có: $x_I = 2$, $y_I = 3$, $x_A = 5$, $y_A = 7$

Thay vào công thức ta được:

$\sqrt{(5-2)^2 + (7-3)^2} = \sqrt{34}$

Vậy bán kính của đường tròn là $\sqrt{34}$.

Phương trình đường tròn © có tâm I(2,3) và bán kính $\sqrt{34}$ là:

$(x-2)^2 + (y-3)^2 = 34$

b) Để tìm phương trình tiếp tuyến của đường tròn © : $(x-1)^2 + ( y+5)^2 =4$, ta cần tìm đạo hàm của phương trình đường tròn tại điểm cần tìm tiếp tuyến.

Ta có phương trình đường tròn chính giữa:

$(x-1)^2 + (y+5)^2 = 2^2$

Đạo hàm hai vế theo x:

$2(x-1) + 2(y+5)y' = 0$

Suy ra:

$y' = -\frac{x-1}{y+5}$

Tại điểm M(x,y) trên đường tròn, ta có:

$(x-1)^2 + (y+5)^2 = 2^2$

Đạo hàm hai vế theo x:

$2(x-1) + 2(y+5)y' = 0$

Suy ra:

$y' = -\frac{x-1}{y+5}$

Vậy tại điểm M(x,y), phương trình tiếp tuyến của đường tròn là:

$y - y_M = y'(x-x_M)$

Thay $y'$ bằng $\frac{-(x-1)}{y+5}$ và $x_M$, $y_M$ bằng 1, -5 ta được:

$y + 5 = \frac{-(x-1)}{y+5}(x-1)$

Simplifying:

$x(y+5) + y(x-1) = 6$

Đường thẳng (d) có phương trình là $3x + 4y - 1 = 0$. Vì tiếp tuyến song song với đường thẳng (d) nên hệ số góc của tiếp tuyến