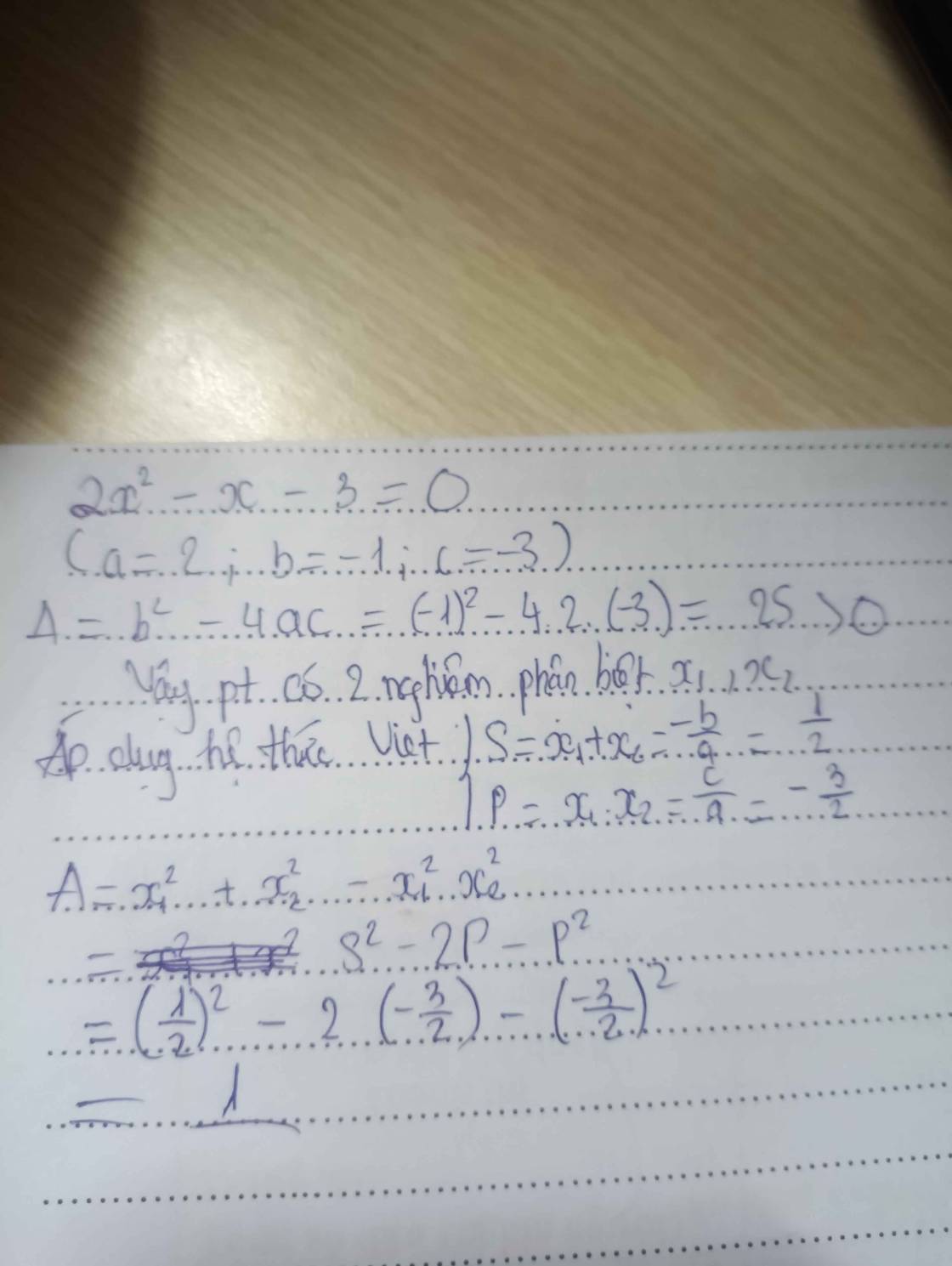x^2-5x+4=0 A= 5x1-x2/x1 - x1-5x2/x2 giúp tớ

Những câu hỏi liên quan
Gọi
x
1
,
x
2
là hai nghiệm của phương trình
x
2
-
5
x
+
6
0
Tính giá trị của
A
5
x
1
+
5
x
2
A.
A...
Đọc tiếp
Gọi x 1 , x 2 là hai nghiệm của phương trình x 2 - 5 x + 6 = 0 Tính giá trị của A = 5 x 1 + 5 x 2
A. A = 125
B. A = 3125
C. A = 150
D. A = 15625
Cho pt : x^2 - 6x + 2n - 3=0 (1)
Tìm n để pt (1) có hai nghiệm phân biệt x1:x2 thỏa
(x1^2 - 5x1 + 2n - 4)(x2^2 - 5x2 + 2n - 4)=-4
\(\Delta'=9-\left(2n-3\right)=12-2n>0\Rightarrow n< 6\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=6\\x_1x_2=2n-3\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên:
\(x_1^2-6x_1+2n-3=0\Leftrightarrow x_1^2-5x_1+2n-4=x_1-1\)
Tương tự ta có: \(x_2^2-5x_2+2n-4=x_2-1\)
Thế vào bài toán:
\(\left(x_1-1\right)\left(x_2-1\right)=-4\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1=-4\)
\(\Leftrightarrow2n-3-6+1=-4\Rightarrow n=2\)
Đúng 2
Bình luận (1)
1. Giải hpt\(\left\{{}\begin{matrix}\dfrac{3y}{x-1}+\dfrac{2x}{y+1}=3\\\dfrac{2y}{x-1}-\dfrac{5x}{y+1}=2\end{matrix}\right.\)
2.Cho PT : x2-6x+2m-3=0
-Tìm m để PT có nghiệm x1,x2 thỏa : (x12-5x1+2m-4)(x22-5x2+2m-4)=2
cho pt x^2 -6x +2m - 3=0 . timf m ddeer pt co hai nghiem phan birt thoa man (x1^2-5x1+2m-4) (x2^2-5x2+2m-4)=2
\(x^2-6x+2m-3=0\)
\(\Delta=b^2-4ac=36-4\left(2m-3\right)=36-8m+12=48-8m\)
Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)\(< =>48-8m>0< =>48>8m< =>6>m\)
Theo Vi-ét ta có :\(\hept{\begin{cases}x_1x_2=\frac{c}{a}=2m-3\\x_1+x_2=\frac{-b}{a}=6\end{cases}}\)là
\(x_1\)là nghiệm phương trình \(x_1^2-6x_1+2m-3=0\)
\(=>x_1^2=3-2m+6x_1\)
\(x_2\)là nghiệm phương trình \(x_2^2-6x_2+2m-3=0\)
\(=>x_2^2=3-2m+6x_2\)
Mà \(\left(x_1^2-5x_1+2m-4\right)\left(x_2^2-5x_2+2m-4\right)=2\)
\(\left(3-2m+6x_1-5x_1+2m-4\right)\left(3-2m+6x_2-5x_2+2m-4\right)=2\)
\(\left(3+x_1-4\right)\left(3+x_2-4\right)=2\)
\(\left(x_1-1\right)\left(x_2-1\right)=2\)
\(x_1x_2-x_1-x_2+1=2\)
\(x_1x_2-\left(x_1+x_2\right)=1\)
\(2m-3-6=1\)
\(2m-9=1\)
\(m=5\)
Vậy m=5
Cho phương trình:x^2-6x+2n-3=0 (với n là tham số ) (1)
1) Giải phương trình (1) với n=4
2) Tìm n để phương trình (1) có hai nghiệm phân biệt x1;x2 thỏa mãn:
(x1^2 -5x1 +2n -4)(x2^2 - 5x2 +2n-4)=-4
Thay n = 4 vào pt (1) ta có
\(x^2-6x+5=0\\ ta.có.a+b+c=1-6+5=0\\ Vậy.pt.có.n_o:\\ x_1=1;x_2=\dfrac{c}{a}=5\)
\(Ta.có:\Delta=b^2-4ac=....=-8n+48\\ Để.pt.\left(1\right).có.1.n_o.phân.biệt.thì.\Delta>0\\ \Leftrightarrow n< 6\)
Vậy m < 6 thì pt (1) có nghiệm phân biệt \(x_1;x_2\) nên theo Vi ét ta có
\(x_1+x_2=\dfrac{-b}{a}=6\\ x_1x_2=\dfrac{c}{a}=2n-3\)
Ta có
\(x^2-6x+2n-3=0\\ \Leftrightarrow x^2-5x+2n-4=x-1\)
Vì x1 x2 là nghiệm pt \(x^2-6x+2n-3=0\) nên x1 x2 là nghiệm PT \(x^2-5x+2n-4=x-1\) nên ta có
\(x_1^2-5x+2x-4=x_1-1.và\\ x_2^2-5x_2+2n-4=x_2-1\\ \Rightarrow\left(x_1^2-5x_1+2n-4\right)\left(x_2^2-5x_2+2n-4\right)=\left(x_1-1\right)\left(x_2-1\right)\)
\(Mà\\ \left(x_1^2-5x_1+2n-4\right)\left(x_2^2-5x_2+2n-4\right)=-4\\ Nên\left(x_1-1\right)\left(x_2-1\right)=-4\\ \Leftrightarrow x_1x_2-\left(x_1+x_2\right)+1=-4\\ \Leftrightarrow2n-3-6+1=-4\\ \Leftrightarrow2n=4\Rightarrow n=2\left(tm\right)\\ ......\left(kl\right)\)
Đúng 2
Bình luận (0)
Cho phương trình \(3x^2-5x+m-2=\)0
Tìm m sao cho phương trình (I) có 2 nghiệm x1,x2 thỏa -5x1 < -5x2 <-2
Cho phương trình: x2 - 6x + 2n - 3 = 0 (với n là tham số). Tìm n để phương trình trên có 2 nghiệm phân biệt x1, x2 thỏa mãn:
(x12 - 5x1 + 2n - 4)(x22 - 5x2 + 2n - 4) = -4
\(\Delta'=9-\left(2n-3\right)>0\Leftrightarrow n< 6\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=6\\x_1x_2=2n-3\end{matrix}\right.\)
Do \(x_1;x_2\) là nghiệm nên:
\(\left\{{}\begin{matrix}x_1^2-6x_1+2n-3=0\\x_2^2-6x_2+2n-3=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1^2-5x_1+2n-4=x_1-1\\x_2^2-5x_2+2n-4=x_2-1\end{matrix}\right.\)
Thay vào bài toán:
\(\left(x_1-1\right)\left(x_2-1\right)=-4\)
\(\Leftrightarrow x_1x_2-\left(x_1+x_2\right)+5=0\)
\(\Leftrightarrow2n-3-6+5=0\Leftrightarrow n=2\)
Đúng 2
Bình luận (2)
Cho phương trình x2 - mx + m - 4 = 0 (x là ẩn ). Chứng minh rằng phương trình có hai nghiệm x1,x2 với mọi m. Tìm tất cả các giá trị nguyên dương của m để (5x1 - 1)(5x2 - 1 ) < 0
\(\Delta=m^2-4\left(m-4\right)=\left(m^2-4m+4\right)+12=\left(m-2\right)^2+12>0;\forall m\)
Suy ra pt luôn có hai nghiệm pb với mọi m
Theo viet có:\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=m-4\end{matrix}\right.\)
\(\left(5x_1-1\right)\left(5x_2-1\right)< 0\)
\(\Leftrightarrow25x_1x_2-5\left(x_1+x_2\right)+1< 0\)
\(\Leftrightarrow25\left(m-4\right)-5m+1< 0\)
\(\Leftrightarrow m< \dfrac{99}{20}\)
Vậy...
Đúng 3
Bình luận (0)
\(\Delta=m^2-4m+16=\left(m-2\right)^2+12>0\)
\(\Rightarrow\) pt luôn có 2 nghiệm phân biệt
Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-4\end{matrix}\right.\)
Ta có: \(\left(5x_1-1\right)\left(5x_2-1\right)=25x_1x_2-5\left(x_1+x_2\right)+1\)
\(=25\left(m-4\right)-5m+1=20m-99\)
\(\Rightarrow20m-99< 0\Rightarrow m< \dfrac{99}{20}\)
Đúng 1
Bình luận (0)
Phương trình : 2x^2-x-3=0 A= x1^2+x2^2-x1^2 x2^2 Giúp tớ đyyy=(
xét ptr \(2x^2-x-3+0\)
△=\(\left(-1\right)^2-4.2.\left(-3\right)=25>0\)
⇒ptr có 2 ngh phân biệt \(x_1;x_2\)
Theo hệt thức viet \(x_1+x_2=\dfrac{1}{2};x_1x_2=\dfrac{-3}{2}\)
Xét A = \(x_1^2+x_2^2-x_1^2x_2^2=\left(x_1+x_2\right)^2-2x_1x_2-x_1^2x_2^2\)
=\(\left(\dfrac{1}{2}\right)^2-2\left(-\dfrac{3}{2}\right)-\left(-\dfrac{3}{2}\right)^2=\dfrac{1}{4}+3-\dfrac{9}{4}=3-2=1\)
Của cậu đây ạ, kh hiểu j thì hỏi tớ nha <3
Đúng 0
Bình luận (0)