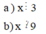tìm a,b ϵ N sao cho 9/56<a/8<b/8<13/28
Những câu hỏi liên quan
![[_khngocc_umeTNhã]](https://hoc24.vn/images/avt/avt156860835_256by256.jpg)
3,Tìm các số tự nhiên m sao cho:
a, m ϵ N(0) và m<36. b, m ϵ N(36) và m > 10
Xác định số phần tử của tập hợp:
a) D = { x ϵ N sao cho x chia 5 dư 2; x < 88 }
b) E = { x ϵ N sao cho x - 15 = 37 }
c) F = { a ϵ N sao cho a x 6 = 4 }
Xem chi tiết
a) D = { x ϵ N sao cho x chia 5 dư 2; x < 88 }
b) E = { x ϵ N sao cho x - 15 = 37 }
c) F = { a ϵ N sao cho a x 6 = 4 }
a) D = {2; 7; 12; ...; 82; 87}
Số phần tử của D:
(87 - 2) : 5 + 1 = 18 (phần tử)
b) x - 15 = 37
x = 37 + 15
x = 52
E = {52}
Số phần tử của E là 1
c) a . 6 = 4
a = 4 : 6
a = 2/3 (loại vì a ∈ ℕ)
F = ∅
Vậy F không có phần tử nào
Đúng 1
Bình luận (0)
a) D = { 2 ; 7 ; 12 ; 17 ; 22 ; 27 ; 32 ; 37 ; 42 ; 47 ; 52 ; 57 ; 62 ; 67 ; 72 ; 77 ; 82 ; 87 }
b) E = { 52 }
c) F = { \(\varnothing\) }
- HokTot -
Đúng 0
Bình luận (0)
Bài 9. Tìm x ϵ N biết:
a) 84⋮x,180⋮x và x≥6
b) x⋮28,x⋮56,x⋮70 và 500<x<600
c) x⋮12 và x<60
a)Vì 84⋮x➩ x∈ƯC(84;180)
180⋮x
Ta có:
24=23.3
180=22.32.5
ƯCLN(...)=22.3=12
ƯC(...)=Ư(12)={1;2;3;4;6;12}
Vì 84⋮x;180⋮x và x≥6
⇔x={6;12}
b)x⋮28;x⋮56;x⋮70➩x∈BC(...)
Ta có:28=22.7
56=23.7
70=2.5.7
BCNN(...)=23.5.7=280
BC(...)=B(280)={0;280;560;840;...}
Vì x⋮28;x⋮56;x⋮70 và 500<x<600
⇔x=280
c)x⋮12➩x=B(12)
B(12)={0;12;24;36;48;60;72;...}
Vì x⋮12 và x<60
⇔ x={0;12;24;48}
Đúng 1
Bình luận (0)
viết 3 số tự nhiên liên tiếp sao cho a ϵ n
a) a;3;4 (a ϵ n )
b)1;a;3 ( a ϵ n* )
Cho A = \(\dfrac{2023.a+b}{2023.a-b}\) với a, b ϵ N; 1 ≤ a ≤ b; 0 ≤ b ≤ 9. Tìm giá trị nhỏ nhất của A
Lời giải:
$A=\frac{2023a+b}{2023a-b}=\frac{(2023a-b)+2b}{2023a-b}$
$=1+\frac{2b}{2023a-b}=1+\frac{2}{2023\frac{a}{b}-1}$
Để $A$ nhỏ nhất thì $\frac{2}{2023.\frac{a}{b}-1}$ nhỏ nhất, tức là $2023\frac{a}{b}-1$ lớn nhất, hay $\frac{a}{b}$ lớn nhất.
Với điều kiện $1\leq a\leq b\leq 9$ và $a,b$ là số tự nhiên thì $\frac{a}{b}$ lớn nhất khi mà $a=b$
Khi đó: $A_{\max}=\frac{2023a+a}{2023a-a}=\frac{2024}{2022}=\frac{1012}{1011}$
Đúng 1
Bình luận (0)
Tìm n ϵ Z sao cho:
a) 25 chia hết cho n + 2
b) 2n + 4 chia hết cho n - 1
c) 1 - 4n chia hết cho n + 3
a) \(25⋮n+2\left(n\in Z\right)\)
\(\Rightarrow n+2\in\left\{-1;1;-5;5;-25;25\right\}\)
\(\Rightarrow n\in\left\{-3;-1;-7;3;-27;23\right\}\)
b) \(2n+4⋮n-1\)
\(\Rightarrow2n+4-2\left(n-1\right)⋮n-1\)
\(\Rightarrow2n+4-2n+2⋮n-1\)
\(\Rightarrow6⋮n-1\)
\(\Rightarrow n-1\in\left\{-1;1;-2;2;-3;3;-6;6\right\}\)
\(\Rightarrow n\in\left\{0;2;-1;3;-2;4;-5;7\right\}\)
c) \(1-4n⋮n+3\)
\(\Rightarrow1-4n+4\left(n+3\right)⋮n+3\)
\(\Rightarrow1-4n+4n+12⋮n+3\)
\(\Rightarrow13⋮n+3\)
\(\Rightarrow n+3\in\left\{-1;1;-13;13\right\}\)
\(\Rightarrow n\in\left\{-4;-2;-15;10\right\}\)
Đúng 4
Bình luận (0)
a) n ϵ{−3;−1;−7;3;−27;23}
b) n ∈{0;2;−1;3;−2;4;−5;7}
c) n ϵ {−4;−2;−15;10}
Đúng 0
Bình luận (0)
Bài 1a) Cho Cfrac{n}{n-2} ( n ϵ Z ; n khác 2)Tìm tất cả các số nguyên n để C là số nguyênb) Cho Dfrac{n}{n+13} ( n ϵ Z ; n khác -13) ( và cũng hỏi như ở câu a)Bài 2a) Cho E frac{3n+5}{n+7} ( n ϵ Z ; n khác -7) Tìm n ϵ Z để E là số nguyênb) Cho F frac{2n+9}{n-5} ( n ϵ Z ; n khác 5) Tìm n ϵ Z để F là số nguyênBài 3a) Cho G frac{n+10}{2n-8} ( n khác 4) Tìm số tự nhiên n để G là số nguyênb) Cho H frac{n-1}{3n-6} ( n khác 2) Tìm n ϵ Z để H là số nguyên
Đọc tiếp
Bài 1
a) Cho C=\(\frac{n}{n-2}\) ( n ϵ Z ; n khác 2)
Tìm tất cả các số nguyên n để C là số nguyên
b) Cho D\(\frac{n}{n+13}\) ( n ϵ Z ; n khác -13) ( và cũng hỏi như ở câu a)
Bài 2
a) Cho E = \(\frac{3n+5}{n+7}\) ( n ϵ Z ; n khác -7) Tìm n ϵ Z để E là số nguyên
b) Cho F = \(\frac{2n+9}{n-5}\) ( n ϵ Z ; n khác 5) Tìm n ϵ Z để F là số nguyên
Bài 3
a) Cho G = \(\frac{n+10}{2n-8}\) ( n khác 4) Tìm số tự nhiên n để G là số nguyên
b) Cho H = \(\frac{n-1}{3n-6}\) ( n khác 2) Tìm n ϵ Z để H là số nguyên
Bài 2:
a: Để E là số nguyên thì \(3n+5⋮n+7\)
\(\Leftrightarrow3n+21-16⋮n+7\)
\(\Leftrightarrow n+7\in\left\{1;-1;2;-2;4;-4;8;-8;16;-16\right\}\)
hay \(n\in\left\{-6;-8;-5;-9;-3;-11;1;-15;9;-23\right\}\)
b: Để F là số nguyên thì \(2n+9⋮n-5\)
\(\Leftrightarrow2n-10+19⋮n-5\)
\(\Leftrightarrow n-5\in\left\{1;-1;19;-19\right\}\)
hay \(n\in\left\{6;4;29;-14\right\}\)
Đúng 0
Bình luận (0)
Cho A= \(\dfrac{19n+1}{2n+3}\) . Tìm n để
a) A là phân số
b) Tìm n ϵ Z để A ϵ z
Cho A = 999- 3 .36 - 6.9 + x với x ϵ N. Tìm điều kiện của x để
a) A chia hết cho 3
b) A không chia hết cho 9
