cíu tui, tui tick cho

Cíu tui zứi ![]() Tui hứa tui tick
Tui hứa tui tick
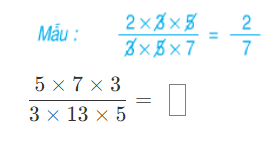
Cíu tui zứi! Tui tick choa nghe!

a: 3/5=9/15
7/3=35/15
b: 9/10=36/40
5/4=50/40
c: 2/7=8/28
5/4=35/28
d: 8/9=16/18
11/6=33/18
e: 6/5=48/40
13/8=65/40
g: 4/5=8/10
3/2=15/10
h: 5/12=10/24
7/8=21/24
i: 11/4=33/12
13/6=26/12
Cíu tui zứi!!! Tui sẽ tick nghe ![]()

Bài 2:
\(a,\dfrac{2\times6\times13}{5\times13\times6}=\dfrac{2}{5}\\ b,\dfrac{8\times11\times13}{11\times13\times16}=\dfrac{8}{16}=\dfrac{8}{8\times2}=\dfrac{1}{2}\\ c,\dfrac{5\times18\times12}{15\times24\times16}=\dfrac{5\times3\times3\times6\times3\times4}{3\times5\times4\times6\times4\times4}=\dfrac{3\times3}{4\times4}=\dfrac{9}{16}\\ d,\dfrac{15\times8\times4}{32\times3\times5}=\dfrac{5\times3\times8\times4}{4\times8\times3\times5}=\dfrac{1}{1}=1\)
Bài 1:
\(a,\dfrac{8}{12}=\dfrac{8:4}{12:4}=\dfrac{2}{3}\\ \dfrac{20}{48}=\dfrac{20:4}{48:4}=\dfrac{5}{12}\\ \dfrac{74}{100}=\dfrac{74:2}{100:2}=\dfrac{37}{50}\\ \dfrac{18}{21}=\dfrac{18:3}{21:3}=\dfrac{6}{7}\\ \dfrac{40}{54}=\dfrac{40:2}{54:2}=\dfrac{20}{27}\\ \dfrac{30}{45}=\dfrac{30:15}{45:3}=\dfrac{2}{3}\\ b,\dfrac{18}{24}=\dfrac{18:6}{24:6}=\dfrac{3}{4}\\ \dfrac{49}{28}=\dfrac{49:7}{28:7}=\dfrac{7}{4}\\ \dfrac{15}{35}=\dfrac{15:5}{35:5}=\dfrac{3}{7}\\ \dfrac{28}{40}=\dfrac{28:4}{40:4}=\dfrac{7}{10}\\ \dfrac{36}{27}=\dfrac{36:9}{27:9}=\dfrac{4}{3}\\ \dfrac{56}{49}=\dfrac{56:7}{49:7}=\dfrac{8}{7}\)
\(c,\dfrac{85}{51}=\dfrac{85:17}{51:17}=\dfrac{5}{3}\\ \dfrac{1515}{2323}=\dfrac{1515:101}{2323:101}=\dfrac{15}{23}\\ \dfrac{39}{26}=\dfrac{39:13}{26:13}=\dfrac{3}{2}\\ \dfrac{323232}{515151}=\dfrac{323232:10101}{515151:10101}=\dfrac{32}{51}\)
Cíu tui zứi -> Tui tick choa nghe! ![]()

Cíu tui vứi...Tui tick choa nhé
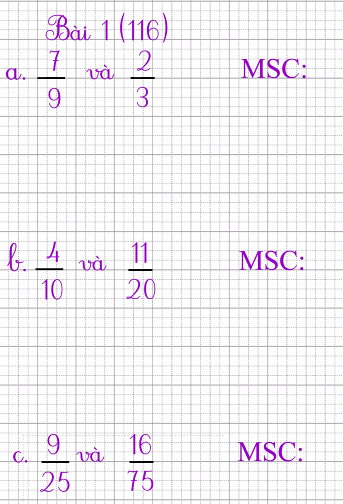
a) MSC là : 9
b) MSC là : 20
c) MSC là : 75
 cíu tui cíu tui
cíu tui cíu tui
1: Xét ΔMNP vuông tại M có MH là đường cao
nên MH^2=HN*HP; MN^2=NH*NP; PM^2=PH*PN
=>MH=căn 3,6*6,4=4,8cm; MN=căn 3,6*10=6cm; PM=căn 6,4*10=8cm
2: MK=8/2=4cm
Xét ΔMNK vuông tại M có tan MNK=MK/MN=4/6=2/3
nên \(\widehat{MNK}\simeq33^041'\)
3: ΔMNK vuông tại M có MF là đường cao
nên NF*NK=NM^2
ΔMNP vuông tại M có MH là đường cao
nên NH*NP=NM^2
=>NF*NK=NH*NP
cíu tui cíu tui ![]()


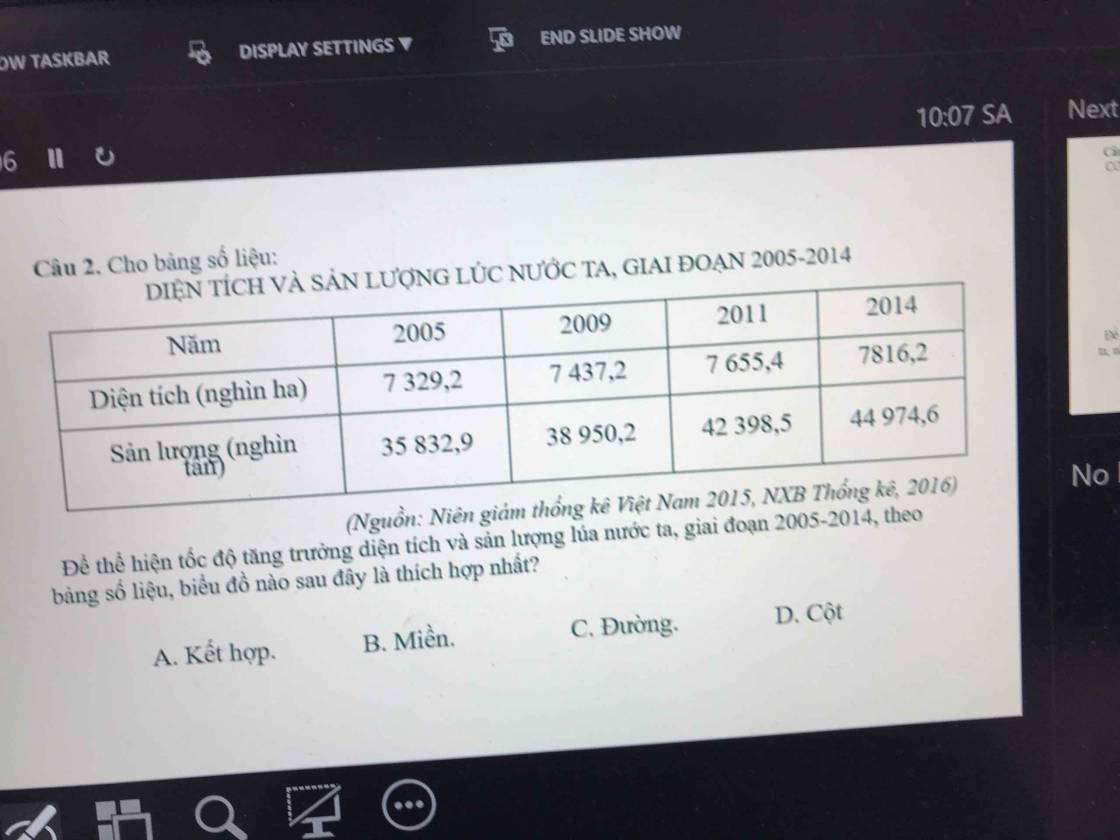
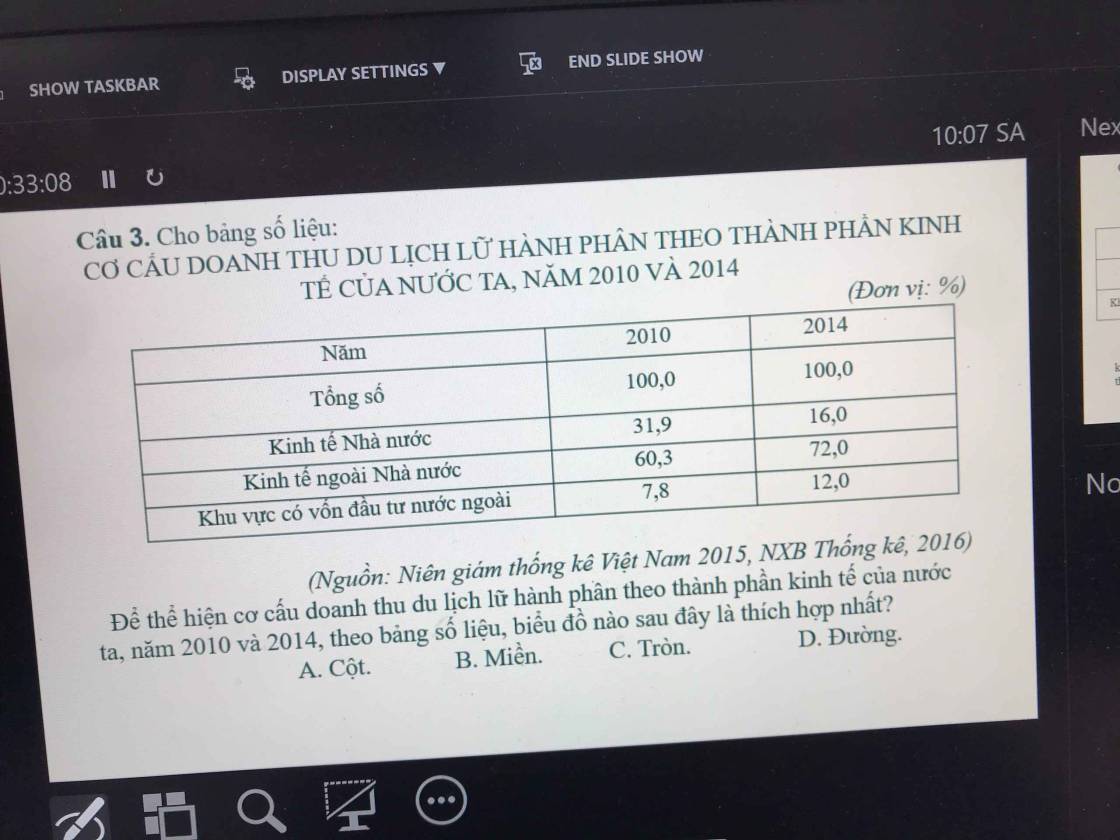
 cíu tui cíu tui
cíu tui cíu tui
a) \(\sqrt[]{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
\(\Leftrightarrow\sqrt[]{3\left(x^2+2x+1\right)+4}+\sqrt{5\left(x^2+2x+1\right)+9}=-\left(x^2+2x+1\right)+5\)
\(\Leftrightarrow\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}=-\left(x+1\right)^2+5\left(1\right)\)
Ta có :
\(\left\{{}\begin{matrix}\sqrt[]{3\left(x+1\right)^2+4}\ge2,\forall x\in R\\\sqrt[]{5\left(x+1\right)^2+9}\ge3,\forall x\in R\end{matrix}\right.\)
\(\Rightarrow VT=\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}\ge5,\forall x\in R\)
\(VP=-\left(x+1\right)^2+5\le5,\forall x\in R\)
Dấu "=" xảy ra thì \(VT=VP=5\)
\(\left(1\right)\Leftrightarrow\left(x+1\right)^2=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Vậy nghiệm của phương trình đã cho là \(x=-1\)

cíu tui cíu tui
a: ΔOHB cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)HB
I là trung điểm của HB
=>\(IH=IB=\dfrac{HB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
ΔOIB vuông tại I
=>\(OB^2=OI^2+IB^2\)
=>\(OB^2=3^2+4^2=25\)
=>OB=5(cm)
=>R=5(cm)
Xét tứ giác MAOI có
\(\widehat{MAO}+\widehat{MIO}=90^0+90^0=180^0\)
=>MAOI là tứ giác nội tiếp đường tròn đường kính MO
Tâm là trung điểm của MO
b: Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó; ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>AH\(\perp\)MB tại H
Xét ΔMAB vuông tại A có AH là đường cao
nên \(MA^2=MH\cdot MB\)
c: Xét (O) có
MA,MK là tiếp tuyến
Do đó: MA=MK
mà OA=OK
nên MO là đường trung trực của AK
\(MA^2=MH\cdot MB\)
MA=MK
Do đó: \(MK^2=MH\cdot MB\)
=>\(\dfrac{MK}{MH}=\dfrac{MB}{MK}\)
Xét ΔMKB và ΔMHK có
\(\dfrac{MK}{MH}=\dfrac{MB}{MK}\)
\(\widehat{KMB}\) chung
Do đó: ΔMKB đồng dạng với ΔMHK
=>\(\widehat{MBK}=\widehat{MHK}\)