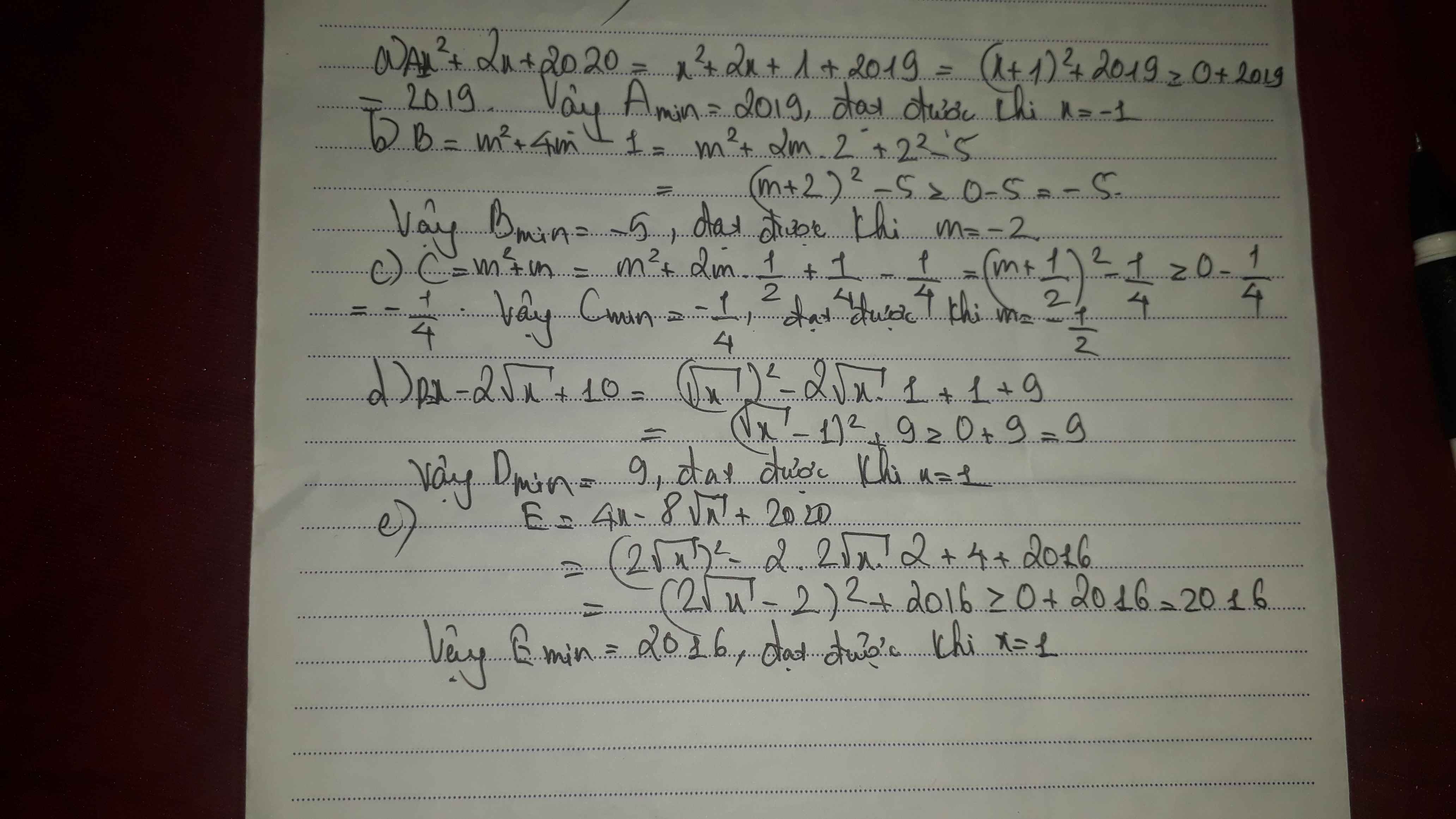Tìm GTNN của biểu thức

Những câu hỏi liên quan
Bài 1) a) (2x+3y)2
b) (25x2-10x+1)
c) (x2-2y)2
d) 16x2-9y2
Bài 2) Tìm GTNN của biểu thức
D= x2+2y2-2xy-6y+2x+2020
Q= 2x2-4xy+y2-4x+6y+10
tìm GTNN của biểu thức : |2x+1|+|x-y+1|, b: |x+2|+1/2.|2x-1| tìm GTLN của biểu thức : |3x+2|-|2020-3x| các cao nhân giúp em với ạ
Tìm GTNN của biểu thức
B=(2x-1) ² +|y-2|+2020
Vì \(\hept{\begin{cases}\left(2x-1\right)^2\ge0\forall x\\\left|y-2\right|\ge0\forall y\end{cases}}\Rightarrow\left(2x-1\right)^2+\left|y-2\right|\ge0\forall x,y\)
\(\Rightarrow\left(2x-1\right)^2+\left|y-2\right|+2020\ge2020\forall x,y\)
Dấu " = " xảy ra khi và chỉ khi \(\hept{\begin{cases}\left(2x-1\right)^2=0\\\left|y-2\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}2x-1=0\\y-2=0\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=2\end{cases}}\)
Vậy GTNN của B bằng 2020 khi x = 1/2,y = 2
Tìm Gtnn của biểu thức: E=2x^2+2xy+2y^2+6x+2020
Ta có: \(E=2x^2+2x\left(y+3\right)+2y^2+2020\)
\(=2\left(x^2+2.x.\frac{\left(y+3\right)}{2}+\frac{\left(y+3\right)^2}{4}\right)+2y^2+2020-\frac{\left(y+3\right)^2}{2}\)
\(=2\left(x+\frac{y+3}{2}\right)^2+\frac{3y^2-6y+4031}{2}\)
\(=2\left(x+\frac{y+3}{2}\right)^2+\frac{3\left(y-1\right)^2+4028}{2}\ge\frac{4028}{2}=2014\)
Đẳng thức xảy ra khi \(\left\{{}\begin{matrix}x=-\frac{y+3}{2}\\y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\)
Vậy...
Đúng 0
Bình luận (0)
tìm giá trị nhỏ nhất của biểu thức A=(x-3)2+2
tìm giá trị nhỏ nhất của biểu thức B=11-x2
+) \(A=\left(x-3\right)^2+2\)
Vì \(\left(x-3\right)^2\)≥0 ∀x
⇒\(A\)≥2 ∀x
Min A=2⇔\(x=3\)
+) \(B=11-x^2\)
Câu này chỉ tìm được max thôi nha
Đúng 1
Bình luận (2)
\(A=\left(x-3\right)^2+2\)
Vì \(\left(x-3\right)^2\ge0\)
\(\Rightarrow\left(x-3\right)^2+2\ge2\)
Vậy GTNN của A là 2 khi x = 3
Đúng 1
Bình luận (0)
tìm gtnn các biểu thức s a)x2+2x+2020
b)m2+4m-1
c)m2+m
d)x-2căn x+10
e)4x-8 căn x +2020
\(a,=x^2+2x+1+2019=\left(x+1\right)^2+2019\ge2019\) dấu"=" xảy ra<=>x=-1
b,\(=m^2+2.2m+4-5=\left(m+2\right)^2-5\ge-5\) dấu"=" xảy ra<=>m=-2
c, \(=x-2\sqrt{x}+10=x-2\sqrt{x}+1+9=\left(\sqrt{x}-1\right)^2+9\ge9\)
dấu"=" xảy ra<=>x=1
b, \(4x-8\sqrt{x}+2020=4x-2.2.2\sqrt{x}+4+2016=\left(2\sqrt{x}-2\right)^2+2016\ge2016\)
dấu"=" xảy ra<=>x=1
Đúng 1
Bình luận (0)
a) Ta có: \(x^2+2x+2020\)
\(=x^2+2x+1+2019\)
\(=\left(x+1\right)^2+2019\ge2019\forall x\)
Dấu '=' xảy ra khi x=-1
b) Ta có: \(m^2+4m-1\)
\(=m^2+4m+4-5\)
\(=\left(m+2\right)^2-5\ge-5\forall m\)
Dấu '=' xảy ra khi m=-2
c) Ta có: \(m^2+m\)
\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}\)
\(=\left(m+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\forall m\)
Dấu '=' xảy ra khi \(m=-\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
tìm GTNN của biểu thức
A=2x2+4y2-4x+4xy+2020
Ta có
A=2x2+4y2-4x+4xy+2020
=(x^2+4y^2+4xy)+(x^2-4x+4)+2016
=(x+2y)^2+(x-2)^2+2016
Thấy
(x+2y)^2>=0 với mọi x,y
(x-2)^2>=0 với mọi x
=>(x+2y)^2+(x-2)^2+2016>=2016 với mọi x,y
Hay Min A>=2016
Dấu "=" xảy ra<=>(x+2y)^2=0 và(x-2)^2=0
<=>x=2;y=-1
Vậy Min A=2016 tại x=2 và y=-1
Đúng 1
Bình luận (0)
D=\(\frac{x^2-2x+2020}{x^2}\) Tìm GTNN của biểu thức
tìm GTNN của biểu thức
M = \(x^2+2y^2+2xy-2x-6y+2020\)
Ta Có :
\(M=x^2+2y^2+2xy-2x-6y+2020\)
\(M=\left(x^2+2xy-2x\right)+2y^2-6y+2020\)
\(M=\left(x^2+2x\left(y-1\right)+\left(y-1\right)^2\right)+2y^2-6y+2020-\left(y-1\right)^2\)
\(M=\left(x+y-1\right)^2+2y^2-6y-y^2+2y-1+2020\)
\(M=\left(x+y-1\right)^2+\left(y^2-4y+4\right)+2015\)
\(M=\left(x+y-1\right)^2+\left(y-2\right)^2+2015\)
Nhận xét : Vì \(\left(x+y-1\right)^2\ge0\) với \(\forall x,y\)
Và \(\left(y-2\right)^2\ge0\) với \(\forall y\)
\(\Rightarrow M\ge2015\) với \(\forall x,y\)
Vậy GTNN của M là 2015 đạt được khi
\(\left\{{}\begin{matrix}x+y-1=0\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
tik mik nha !!!
Đúng 0
Bình luận (0)
x2 + 2y2 + 2xy - 2x - 6y + 2020
= x2 + 2xy + y2 + y2 - 2x - 6y + 2020
= (x+y)2 + y2 - 4y + 4 - 2x - 2y + 2016
= (x+y)2 + (y-z)2 - 2(x+y) + 2016
= (x+y)2 - 2(x+y) + 1 + (y-z)2 + 2015
= (x+y-1)2 + (y-z)2 + 2015 ≥ 2015
Dấu "=" xảy ra khi x+y-1=0 và y-2=0
(=) x=-1 y=2
Vậy GTNN của biểu thức trên là 2015 khi x=-1 và y=2
Chúc bạn học tốt ^^
Đúng 0
Bình luận (0)