Các bn ơi cho mình hỏi
Cho ΔABC có \(\widehat{B}\) = 750; \(\widehat{C}\) = 600 .Trên tia đối của tia CB lấy điểm D sao cho CD = \(\frac{1}{2}\)BC . Tính \(\widehat{ADC}\)
Những câu hỏi liên quan
cho tam giác ABC vuông tại C có \(\widehat{A}< \widehat{B}\). gọi I, O thứ tự là tâm đường tròn nội tiếp, ngoại tiếp ΔABC. biết ΔBIO vuông . tính tỉ số các cạnh của ΔABC
Cho \(\Delta ABC\)cân tại A có \(\widehat{A}=120^0\),phân giác AD.Từ B kẻ đường thẳng song song AD cắt CA tại E.
a,C/m tg ADE đều
b,So sánh các cạnh của tam giác BEC
giúp mình vs các bn ơi
Cho mình hỏi
Cho góc nhọn xOy.Trên Ox lấy Avà B sao cho OA<OB.Trên Oy lấy C và D sao cho OC<OD Chứng minh rằng: AB+CD<AD+BC
Ai làm đc giúp mình với 
Gọi I là giao của AD và BC
IA+IB>AB
IC+ID>CD
=>AB+CD<AD+BC
Đúng 0
Bình luận (0)
Cho ΔABC = ΔMNE, biết AB = 4cm, NE = 3cm, \(\widehat{A}\) = \(50^o\). Tính MN, BC, \(\widehat{M}\)
Mọi người giúp mình giải bài này với
MN=AB=4cm
NE=BC=3cm
\(\widehat{M}=\widehat{A}=50^0\)
Đúng 1
Bình luận (0)
Vì ΔABC = ΔMNE
nên:
+)MN=AB=4cm
+)NE=BC=3cm
+)góc A=góc M=50 độ
vậy:
+)MN=4cm
+)BC=3cm
+)góc M=50 độ
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A có AB =3cm AC =4cm, kẻ đường cao AH (H ∈ BC)
a) Tính BC.
b) So sánh \(\widehat{B}\) và \(\widehat{C}\); HB và HC.
Help me câu b).
Vì ΔABC vuông tại A
==> BC2 = AC2 +AB2 ( Định lý Pitago )
BC2 = 42 + 32
BC2 = 27
==> BC = √27
Đúng 0
Bình luận (0)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Vậy: BC=5cm
Đúng 0
Bình luận (0)
b) Xét ΔABC có AC>AB(4cm>3cm)
mà góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh AB là \(\widehat{ACB}\)
nên \(\widehat{B}>\widehat{C}\)(Định lí quan hệ giữa cạnh và góc đối diện trong tam giác)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
26 tháng 4 2021 lúc 18:27
Cho ΔABC vuông tại A, biết AB 6cm; AC 8cm. a) Tính độ dài cạnh BC, so sánh widehat{B} và widehat{C}. b) Vẽ trung tuyến AM của ΔABC. Trên tia đối của tia MA lấy điểm E sao cho ME MA. Chứng minh: ΔMAB ΔMEC và widehat{ACE} 90 độ. c) Gọi H là trung điểm của cạnh AC, chứng minh: HB HE. d) HB cắt AE tại P, HE cắt BC tại Q, chứng minh: ΔHPQ cân.
Đọc tiếp
Cho ΔABC vuông tại A, biết AB = 6cm; AC = 8cm.
a) Tính độ dài cạnh BC, so sánh \(\widehat{B}\) và \(\widehat{C}\).
b) Vẽ trung tuyến AM của ΔABC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh: ΔMAB = ΔMEC và \(\widehat{ACE}\) = 90 độ.
c) Gọi H là trung điểm của cạnh AC, chứng minh: HB = HE.
d) HB cắt AE tại P, HE cắt BC tại Q, chứng minh: ΔHPQ cân.
cho Δ ABC = ΔMNQ Và \(\widehat{A}\) = 650 \(\widehat{N}\)= 400 thì số đo của \(\widehat{C}\) là:
A. 400 B. 850 C. 650 D. 750
Xem thêm câu trả lời
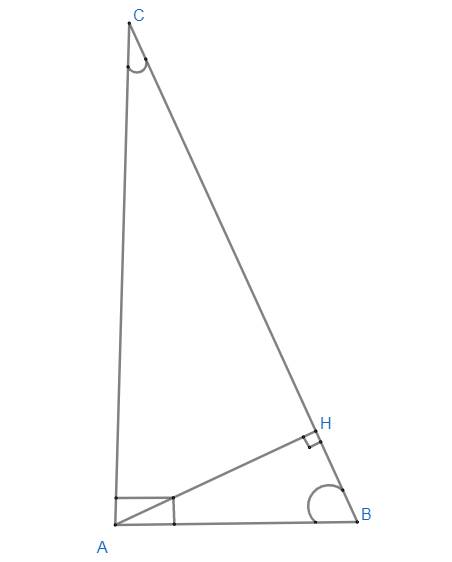
Cho ΔABC vuông tại A (AB < AC)
Kẻ \(AH\perp BC\) tại H
a) Chứng minh \(\widehat{ABC}\) = \(\widehat{HAC}\)
b) Chứng minh \(\widehat{ACB}\) = \(\widehat{HAB}\)
a)
Xét 2 tam giác vuông ABC và HAC có:
\(\widehat{C}\) chung
=> tg ABC \(\sim\) td HAC (g.g)
=> \(\widehat{ABC}=\widehat{HAC}\)
b)
Xét 2 tg vuông ACB và HAB có:
\(\widehat{B}\) chung
=> tg ACB \(\sim\) tg HAB (g.g)
=> \(\widehat{ACB}=\widehat{HAB}\)
Đúng 2
Bình luận (2)
Trong ΔABC,ΔABC, kẻ AH⊥BC(H∈BC) sao cho \(\widehat{BAH}\)= \(2\widehat{CAH}\). Tính \(\widehat{B}\); \(\widehat{C}\) biết \(\widehat{A}=72^O\). (VẼ CẢ HÌNH)