 giải dùm câu 3 vs plss
giải dùm câu 3 vs plss

Những câu hỏi liên quan
Giúp mik câu 5 vs, plss

giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Đúng 3
Bình luận (1)
Câu 2 đề thiếu yêu cầu
Câu 9:
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)
Đúng 2
Bình luận (0)
Giải dùm e mấy câu tích phân vs ạ
11. \(I=\int\limits^2_1x\sqrt{x^2+1}dx\)
Đặt \(\sqrt{x^2+1}=t\Leftrightarrow x^2=t^2-1\Rightarrow xdx=tdt\) ; \(\left\{{}\begin{matrix}x=1\Rightarrow t=\sqrt{2}\\x=2\Rightarrow t=\sqrt{5}\end{matrix}\right.\)
\(I=\int\limits^{\sqrt{5}}_{\sqrt{2}}t.tdt=\int\limits^{\sqrt{5}}_{\sqrt{2}}t^2dt=\dfrac{1}{3}t^3|^{\sqrt{5}}_{\sqrt{2}}=\dfrac{1}{3}\left(5\sqrt{5}-2\sqrt{2}\right)\)
12. Đặt \(\sqrt[3]{8-4x}=t\Rightarrow x=\dfrac{8-t^3}{4}\Rightarrow dx=-\dfrac{3}{4}t^2dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=2\\x=2\Rightarrow t=0\end{matrix}\right.\)
\(I=\int\limits^0_2t.\left(-\dfrac{3}{4}t^2dt\right)=\dfrac{3}{4}\int\limits^2_0t^3dt=\dfrac{3}{16}t^4|^2_0=3\)
13. Đặt \(\sqrt{3-2x}=t\Rightarrow x=\dfrac{3-t^2}{2}\Rightarrow dx=-tdt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=\sqrt{3}\\x=1\Rightarrow t=1\end{matrix}\right.\)
\(I=\int\limits^1_{\sqrt{3}}\dfrac{-tdt}{t}=\int\limits^{\sqrt{3}}_1dt=t|^{\sqrt{3}}_1=\sqrt{3}-1\)
Đúng 1
Bình luận (0)
Giải dùm mik mấy câu này vs ạk
Thank nhìu

1..so I tired
2..I tried my best
3.. the most beautiful place in the world
4..tease the dog
1The children are playing football at the moment
2I haven't met Lan for a long time
Đúng 1
Bình luận (0)
Ảnh 1:
1. I stayed up late, so I am tired
2. I did not pass my exam although I tried my best
3. My homeland is the best beautiful place in the world
4. Don't tease the dog
Đúng 1
Bình luận (0)
Ảnh 2:
1. The children are playing football at the moment
2. I hasn't met Lan for a long time
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Giải dùm me câu này nha ns các giải chi tiết để me áp dụng các câu khác vs😆
tìm n nguyên để gtri bth nguyên hả bạn ?
\(B=\dfrac{2n-6}{n-1}=\dfrac{2\left(n-1\right)-4}{n-1}=2-\dfrac{4}{n-1}\Rightarrow n-1\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
| n-1 | 1 | -1 | 2 | -2 | 4 | -4 |
| n | 2 | 0 | 3 | -1 | 5 | -3 |
Đúng 0
Bình luận (0)
Ta có 2n-6\(\in Z\)
n-1\(\in\)Z
n-1\(\ne0\)
\(\Rightarrow\) \(\dfrac{2n-6}{n-1}\)là phân số
Để B có giá trị nguyên thì 2n-6\(⋮\)n-1
2n-6\(⋮\)n-1
n-1\(⋮\)n-1\(\Rightarrow\)2(n-1)\(⋮\)n-1\(\Rightarrow\)2n-2\(⋮\)n-1
\(\Rightarrow\) (2n-2)\(-\left(2n-6\right)\)\(⋮\)n-1
\(\Rightarrow\)2n-2-2n+6\(⋮\)n-1
\(\Rightarrow\)(2n-2n)+(6-2) \(⋮\)n-1
\(\Rightarrow\) 4 \(⋮\)n-1
\(\Rightarrow n-1\) là ước của 4
\(\Rightarrow\)n-1\(\in\){1;-1;2;-2;4;-4}
\(\Rightarrow\)n\(\in\){2;0;3;-1;5;-3}
Đúng 0
Bình luận (0)
tìm x,y biết x+y=10 và x/y =1,5 ai giúp câu này vs plss.
\(\dfrac{x}{y}=1,5\Rightarrow x=1,5y\)
\(x+y=10\Rightarrow1,5y+y=10\Rightarrow2,5y=10\Rightarrow y=10:2,5=4\)
\(\Rightarrow x=10-4=6\)
Vậy \(\left\{{}\begin{matrix}x=6\\y=4\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giúp em giải câu 11. 13 15 vs ăn
Giải thích dùm em luôn
Em cảm ơn 

Đề mờ quá, bạn chụp lại được không
Đúng 0
Bình luận (1)
11.
\(y'=3x^2+6x=3x\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
\(y''=6x+6\)
\(\Rightarrow\left\{{}\begin{matrix}y''\left(0\right)=6>0\\y''\left(-2\right)=-6< 0\end{matrix}\right.\) \(\Rightarrow x=0\) là điểm cực tiểu
\(\Rightarrow y_{CT}=y\left(0\right)=-3\)
Đúng 0
Bình luận (0)
13.
\(y'=-4x^3+4x=-4x\left(x^2-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
\(y''=-12x^2+4\)
\(\Rightarrow\left\{{}\begin{matrix}y''\left(0\right)=0>0\\y''\left(1\right)=y''\left(-1\right)=-8< 0\end{matrix}\right.\)
\(\Rightarrow x=0\) là điểm cực tiểu
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
giải dùm em câu 1,3,4,6 vs ạ em cảm ơn và em cần gấp lắm
1.
\(y'=x^2-6x+5=0\Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Dấu của y' trên trục số:

Hàm đồng biến trên các khoảng \(\left(-\infty;1\right)\) và \(\left(5;+\infty\right)\)
Hàm nghịch biến trên \(\left(1;5\right)\)
3.
TXĐ: \(D=R\backslash\left\{2\right\}\)
\(y'=\dfrac{-5}{\left(x-2\right)^2}< 0;\forall x\in D\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
Đúng 0
Bình luận (0)
4.
\(y'=4x^3+4x=4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
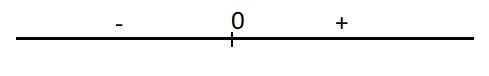
Hàm đồng biến trên \(\left(0;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\)
6.
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-1;1\right)\)
Đúng 0
Bình luận (0)
giúp em 3 bài này gấp vs ạ!plss
Câu 5:
\(\left\{{}\begin{matrix}x^2+y^2=4\left('\right)\\x-y-xy=2\left(''\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2+2xy=4\\x-y-xy=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2+2xy=4\left(1\right)\\2\left(x-y\right)-2xy=4\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)+\left(2\right)\) ta được:
\(\left(x-y\right)^2+2\left(x-y\right)=8\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-y\right)+1-9=0\)
\(\Leftrightarrow\left(x-y+1\right)^2-9=0\)
\(\Leftrightarrow\left(x-y-2\right)\left(x-y+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-y=2\\x-y=-4\end{matrix}\right.\)
Với \(x-y=2\) Thay vào \(\left(''\right)\) ta được:
\(2-xy=2\Rightarrow xy=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-2\\y=0\Rightarrow x=2\end{matrix}\right.\)
Với \(x-y=4\Rightarrow x=4+y\) Thay vào \(\left('\right)\) ta được:
\(\left(4+y\right)^2+y^2=4\)
\(\Leftrightarrow y^2+8y+16+y^2-4=0\)
\(\Leftrightarrow2y^2+8y+12=0\)
\(\Leftrightarrow y^2+4y+6=0\)
\(\Leftrightarrow\left(y+2\right)^2+2=0\) (phương trình vô nghiệm).
Vậy hệ phương trình đã cho có nghiệm \(\left(x,y\right)\in\left\{\left(2;0\right),\left(0;-2\right)\right\}\)
Đúng 0
Bình luận (0)
Câu 6: \(\left\{{}\begin{matrix}2xy+y^2=3\left('\right)\\x^2+5xy=6\left(''\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4xy+2y^2=6\left(1\right)\\x^2+5xy=6\left(2\right)\end{matrix}\right.\)
Lấy \(\left(2\right)-\left(1\right)\) ta được:
\(x^2+xy-2y^2=0\)
\(\Leftrightarrow x^2-y^2+xy-y^2=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)+y\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+2y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x=-2y\end{matrix}\right.\)
Với \(x=y\) Thay vào \(\left('\right)\) ta được:
\(2y.y+y^2=3\)
\(\Leftrightarrow y=\pm1\Rightarrow x=\pm1\).
Với \(x=-2y\) Thay vào \(\left('\right)\) ta được:
\(2.\left(-2y\right).y+y^2=3\)
\(\Leftrightarrow y^2=-1\) (phương trình vô nghiệm)
Vậy hệ phương trình đã cho có nghiệm \(\left(x,y\right)\in\left\{\left(1;1\right),\left(-1;-1\right)\right\}\)
Đúng 0
Bình luận (0)
Câu 4: \(Đk:x>-1;y>-\dfrac{1}{2}\)
Đặt \(\left\{{}\begin{matrix}a=\dfrac{1}{\sqrt{x+1}}\left(a>0\right)\\b=\dfrac{1}{\sqrt{2y+1}}\left(b>0\right)\end{matrix}\right.\)
Hệ phương trình đã cho trở thành:
\(\left\{{}\begin{matrix}2a+b=5\\3a+2b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a+2b=10\\3a+2b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a+b=5\\a=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{\sqrt{x+1}}=1\\\dfrac{1}{\sqrt{2y+1}}=3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{x+1}=1\\\sqrt{2y+1}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+1=1\\2y+1=\dfrac{1}{9}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-\dfrac{4}{9}\end{matrix}\right.\left(nhận\right)\)
Đúng 0
Bình luận (0)