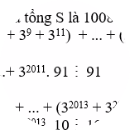Ta có: \(\left\{{}\begin{matrix}x^2+2y+1=0\\y^2+2z+1=0\\z^2+2x+1=0\end{matrix}\right.\)

\(\Rightarrow x^2+2y+1+y^2+2z+1+z^2+2x+1=0\)

\(\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2+\left(z+1\right)^2=0\)

\(\Rightarrow x=y=z=-1\)(do \(\left(x+1\right)^2,\left(y+1\right)^2,\left(z+1\right)^2\ge0\forall x,y,z\))

a) \(A=x^{2020}+y^{2020}+z^{2020}=\left(-1\right)^{2020}+\left(-1\right)^{2020}+\left(-1\right)^{2020}=1+1+1=3\)

b) \(B=\dfrac{1}{x^{2020}}+\dfrac{1}{y^{2020}}+\dfrac{1}{z^{2020}}=\dfrac{1}{\left(-1\right)^{2020}}+\dfrac{1}{\left(-1\right)^{2020}}+\dfrac{1}{\left(-1\right)^{2020}}=\dfrac{1}{1}+\dfrac{1}{1}+\dfrac{1}{1}=3\)

\(\left(2x-1\right)^{2020}+\left(y-\frac{2}{5}\right)^{2022}+\left|x+y-z\right|=0\)

Ta có : \(\left(2x-1\right)^{2020}\ge0\forall x;\left(y-\frac{2}{5}\right)^{2022}\ge0\forall x;\left|x+y-z\right|\ge0\forall x;y;z\)

Dấu bằng xảy ra <=> \(x=\frac{1}{2};y=\frac{2}{5};z=x+y=\frac{1}{2}+\frac{2}{5}=\frac{9}{10}\)

Vậy \(x=\frac{1}{2};y=\frac{2}{5};z=\frac{9}{10}\)

\(a,2^x+2^{x+3}=144\\ 2^x.\left(1+2^3\right)=144\\ 2^x.9=144\\ 2^x=144:9\\ 2^x=16=2^4\\ vậy:x=4\)

\(b,\left(x-5\right)^{2022}=\left(x-5\right)^{2021}\\ Vì:\left[{}\begin{matrix}0^{2022}=0^{2021}\\1^{2022}=1^{2021}\end{matrix}\right.\\ Vậy:\left[{}\begin{matrix}x-5=0\\x-5=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=6\end{matrix}\right.\)

\(c,\\ \left(2x+1\right)^3=9.81\\ \left(2x+1\right)^3=3^2.3^4\\ \left(2x+1\right)^3=3^6\\ \left(2x+1\right)^3=\left(3^2\right)^3=9^3\\ Vậy:2x+1=9\\ 2x=9-1\\ 2x=8\\ x=\dfrac{8}{2}\\ x=4\)

B

B

a: \(\left(2x-y+7\right)^{2022}>=0\forall x,y\)

\(\left|x-1\right|^{2023}>=0\forall x\)

=>\(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}>=0\forall x,y\)

mà \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}< =0\forall x,y\)

nên \(\left(2x-y+7\right)^{2022}+\left|x-1\right|^{2023}=0\)

=>\(\left\{{}\begin{matrix}2x-y+7=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2x+7=9\end{matrix}\right.\)

\(P=x^{2023}+\left(y-10\right)^{2023}\)

\(=1^{2023}+\left(9-10\right)^{2023}\)

=1-1

=0

c: \(\left|x-3\right|>=0\forall x\)

=>\(\left|x-3\right|+2>=2\forall x\)

=>\(\left(\left|x-3\right|+2\right)^2>=4\forall x\)

mà \(\left|y+3\right|>=0\forall y\)

nên \(\left(\left|x-3\right|+2\right)^2+\left|y+3\right|>=4\forall x,y\)

=>\(P=\left(\left|x-3\right|+2\right)^2+\left|y-3\right|+2019>=4+2019=2023\forall x,y\)

Dấu '=' xảy ra khi x-3=0 và y-3=0

=>x=3 và y=3

lỗi rồi

lỗi

lỗi r

\(a,\left\{{}\begin{matrix}\left|x-3y\right|\ge0\\\left|y+4\right|\ge0\end{matrix}\right.\Rightarrow VT\ge0\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-3y=0\\y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3y=-12\\y=-4\end{matrix}\right.\)

\(b,Sửa:\left|x-y-5\right|+\left(y+3\right)^2=0\\ \left\{{}\begin{matrix}\left|x-y-5\right|\ge0\\\left(y+3\right)^2\ge0\end{matrix}\right.\Rightarrow VT\ge0\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-y-5=0\\y+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+5=2\\y=-3\end{matrix}\right.\)

\(c,\left\{{}\begin{matrix}\left|x+y-1\right|\ge0\\\left(y-2\right)^4\ge0\end{matrix}\right.\Rightarrow VT\ge0\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x+y-1=0\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1-y=-1\\y=2\end{matrix}\right.\)

\(d,\left\{{}\begin{matrix}\left|x+3y-1\right|\ge0\\3\left|y+2\right|\ge0\end{matrix}\right.\Rightarrow VT\ge0\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x+3y-1=0\\y+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1-3y=7\\y=-2\end{matrix}\right.\)

\(e,Sửa:\left|2021-x\right|+\left|2y-2022\right|=0\\ \left\{{}\begin{matrix}\left|2021-x\right|\ge0\\\left|2y-2022\right|\ge0\end{matrix}\right.\Rightarrow VT\ge0\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}2021-x=0\\2y-2022=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2021\\y=1011\end{matrix}\right.\)

Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)

Do đó đề bài xảy ra khi và chỉ khi :

\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)

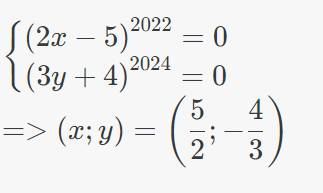Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?