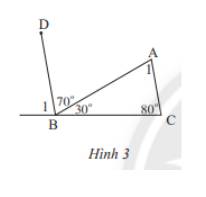
Quan sát Hình 3
a) Tính B1
b) Chứng minh rằng AC // BD
c) Tính A2
Quan sát Hình 54, trong đó Cx song song với AB.
a) Tính số đo góc BCx.
b) Chứng minh rằng Cx song song với DE.
c) Tính số đo góc BCD.

a) Vì Cx // AB nên \(\widehat {ABC} = \widehat {BCx}\) ( 2 góc so le trong), mà \(\widehat {ABC} = 45^\circ \Rightarrow \widehat {BCx} = 45^\circ \)
b) Vì AE \( \bot \) AB; AE \( \bot \) ED nên AB // ED (2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
Mà Cx // AB (gt)
\( \Rightarrow \) Cx // ED (2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau)
c) Vì Cx // ED nên \(\widehat {EDC} = \widehat {DCx}\) ( 2 góc so le trong), mà \(\widehat {EDC} = 60^\circ \Rightarrow \widehat {DCx} = 60^\circ \)
Vì tia Cx nằm trong góc BCD nên \(\widehat {BCD} = \widehat {BCx} + \widehat {DCx} = 45^\circ + 60^\circ = 105^\circ \)
Quan sát Hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC.
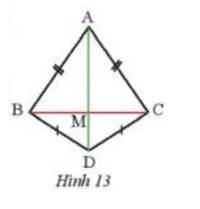
Xét tam giác ABD và tam giác ACD có :
AB = AC ( giả thiết )
BD = CD ( giả thiết )
AD cạnh chung
\( \Rightarrow \Delta ABD =\Delta ACD (c-c-c)\)
\( \Rightarrow \)\(\widehat {BAD} = \widehat {CAD}\)( 2 góc tương ứng )
Xét tam giác ABM và ta giác ACM có :
AB = AC ( giả thiết )
AM cạnh chung
\(\widehat {BAD} = \widehat {CAD}\)( chứng minh trên )
\(\Delta ABM=\Delta ACM (c-g-c)\)
\(\Rightarrow MC = MB\) ( 2 cạnh tương ứng )
\( \Rightarrow \) M là trung điểm BC
Quan sát hình bên, đường thẳng Gh cắt hai đường thẳng AC , DF lần lượt tại B , E Tia BM là tia phân giác của góc ABE
a) chứng minh rằng góc CBG = 2 góc ABM
b)giả sử góc ABG = góc HEF
Chứng minh rằng AC song song với DF
Quan sát hình bên, đường thẳng Gh cắt hai đường thẳng AC , DF lần lượt tại B , E Tia BM là tia phân giác của góc ABE
a) chứng minh rằng góc CBG = 2 góc ABM
b)giả sử góc ABG = góc HEF
Chứng minh rằng AC song song với DF
Cho hình thang vuông ABCD có đường cao AB. Biết AD = 3a. BC =4a và góc BDC= 1 vuông. Tính AB, CD, AC
Cho tam giác ABC vuông tại A, đường trung tuyến CK
a) Cho biết BC=10cm AC=6cm. tính độ dài đoạn thẳng AB
b)trên Tia đối của tia MC lấy điểm D sao cho KD=KC. chứng minh rằng tam Giác KAC= tam giác KBD và AC = BD
c) Chứng Minh Rằng AC+BC>2CK
áp dụng định lý py-ta-go cho ΔABC vuông tại A ta có:
BC2=AB2+AC2
102=62+AB2
100=36+AB2
hay AB2=100-36=64
⇒AB=\(\sqrt{64}\)=8
vậy AB=8
xét ΔACK và ΔBDK có:
KD=KC(giả thuyết)
KA=KB(CK là trung tuyến)
\(\widehat{AKC}\)=\(\widehat{BKD}\)(2 goc đối đỉnh)
⇒ΔACK=ΔBDK(c-g-c)
⇒AC=BD(2 cạnh tương ứng)
xét ΔCBD có
BC+DC>CD(bất đẳng thức tam giác)
Mà DC=2KC;AC=BD
⇒AC+BC>2CK(điều phải chứng minh)
Quan sát Hình 22, chứng minh rằng \(MN//BC\).
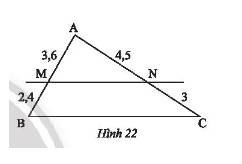
Ta có:
\(\frac{{AM}}{{MB}} = \frac{{3,6}}{{2,4}} = \frac{3}{2}\);\(\frac{{AN}}{{NC}} = \frac{{4,5}}{3} = \frac{3}{2}\).
Vì \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} = \frac{3}{2}\)
Theo định lí Thales đảo trong \(\Delta ABC\), ta có \(MN//BC\) (điều phải chứng minh).
cho số thực a chứng minh rằng: a2 +3a+4≥ 5a+3
\(\)
đây nhé bn
\(a 2 + 3 a + 4 ≥ 5 a + 3 ⇔ a 2 − 2 a + 1 ≥ 0 ⇔ ( a − 1 ) 2 ≥ 0\)
Cho tam giác ABC vuông tại A, AC=3cm BC=4cm; phân giác BD cắt đường cao AH tại K.
a) Tính diện tích hình tam giác ABC
b) tính BD
c) chứng minh tam giác ABD cân
Sửa đề: AC=4cm; AB=3cm
a: \(S_{ABC}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=4/8=0,5
=>AD=1,5cm; CD=2,5cm
\(BD=\sqrt{1.5^2+3^2}=\dfrac{3}{2}\sqrt{5}\left(cm\right)\)
Bài 3A. Cho ΔABC cân tại B. Kẻ BH ⊥ AC tại H. Cho AB = 5cm, BH = 4cm.
a) Tính độ dài đoạn AH;
b) Chứng minh rằng: ΔABH = ΔCBH
c) Kẻ HI ⊥ AB tại I, kẻ HK ⊥ BC tại K.Chứng minh rằng: HI = HK;
d) Chứng minh rằng: IK ⫽ AC.
a: Xét ΔBHA vuông tại H có
\(BA^2=BH^2+HA^2\)
hay AH=3(cm)
b: Xét ΔABH vuông tại H và ΔCBH vuông tại H có
BA=BC
BH chung
Do đó: ΔABH=ΔCBH
c: Xét ΔBIH vuông tại I và ΔBKH vuông tại K có
BH chung
\(\widehat{IBH}=\widehat{KBH}\)
Do đó: ΔBIH=ΔBKH
Suy ra: HI=HK
d: Xét ΔBAC có BI/BA=BK/BC
Do đó: IK//AC