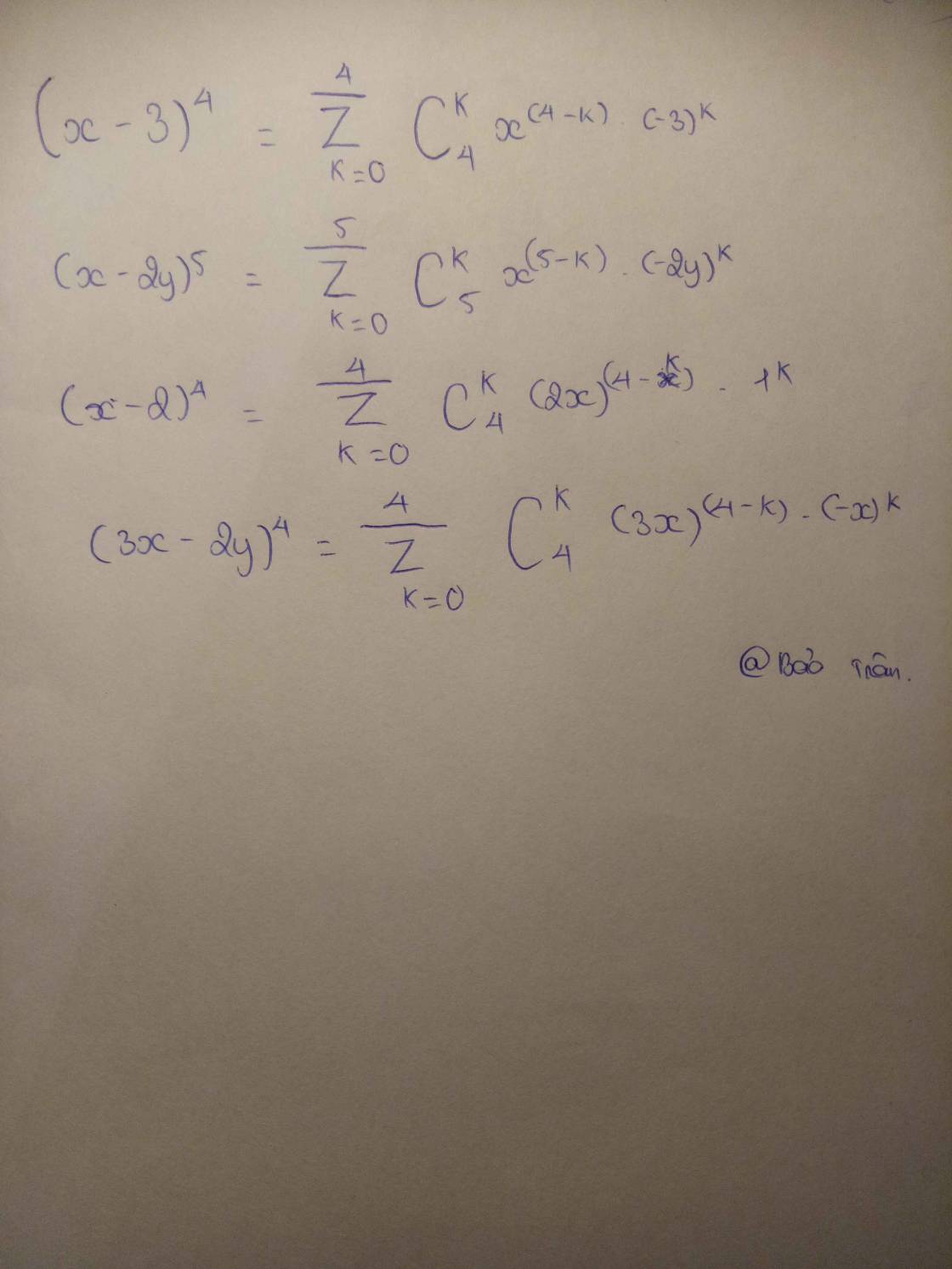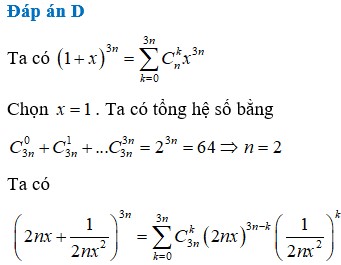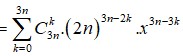Khai triển nhị thức (1-x/2)^4

Những câu hỏi liên quan
khai triển nhị thức Newton
\(\left(x^2+\dfrac{1}{x}\right)^4\)
(x^2+1/x)^4
\(=C^0_4\cdot\left(x^2\right)^4+C^1_4\cdot\left(x^2\right)^3\cdot\left(\dfrac{1}{x}\right)+C^2_4\cdot\left(x^2\right)^2\cdot\left(\dfrac{1}{x}\right)^2+C^3_4\cdot\left(x^2\right)^1\cdot\left(\dfrac{1}{x}\right)^3+C^4_4\cdot\left(x^2\right)^0\cdot\left(\dfrac{1}{x}\right)^4\)
=x^8+4x^5+6x^3+4/x+1/x^4
Đúng 1
Bình luận (1)
khai triển các đa thức sau bằng nhị thức Newton
(x-3)^4 , (x-2y)^5 , (2x+1)^4 , (x-2)^4 , (3x-2y)^4
Cho nhị thức
x
+
1
x
n
,
x
≠
0
trong tổng số các hệ số của khai triển nhị thức đó là 1024. Khi đó số hạng không chứa x trong khai triển nhị thức đã cho bằng A. 252 B. 125 C. -252 D. 525
Đọc tiếp
Cho nhị thức x + 1 x n , x ≠ 0 trong tổng số các hệ số của khai triển nhị thức đó là 1024. Khi đó số hạng không chứa x trong khai triển nhị thức đã cho bằng
A. 252
B. 125
C. -252
D. 525
Câu 2. Cho biểu thức Q= (xy - 1) ^ prime .a) Viết khai triển biểu thức 2 bằng nhị thức Newton.b) Tìm số hạng có chứa x ^ 2 * y ^ 2 trong khai triển trên.
Tổng các hệ số nhị thức Niu – tơn trong khai triển
(
1
+
x
)
3
n
bằng 64. Số hạng không chứa x trong khai triển
(
2
n
x
+
1
...
Đọc tiếp
Tổng các hệ số nhị thức Niu – tơn trong khai triển ( 1 + x ) 3 n bằng 64. Số hạng không chứa x trong khai triển ( 2 n x + 1 2 n x 2 ) 3 n là
A. 360
B. 210
C. 250
D. 240
Sử dụng công thức nhị thức Newton, khai triển các biểu thức sau:
a) \({\left( {3x + y} \right)^4}\)
b) \({\left( {x - \sqrt 2 } \right)^5}\)
a) \({\left( {3x + y} \right)^4} = {\left( {3x} \right)^4} + 4.{\left( {3x} \right)^3}y + 6.{\left( {3x} \right)^2}{y^2} + 4.\left( {3x} \right){y^3} + {y^4}\)
\( = 81{x^4} + 108{x^3}y + 54{x^2}{y^2} + 12x{y^3} + {y^4}\)
b) \(\begin{array}{l}{\left( {x - \sqrt 2 } \right)^5} = \left( {x + (-\sqrt 2) } \right)^5 ={x^5} + 5.{x^4}.\left( { - \sqrt 2 } \right) + 10.{x^3}.{\left( { - \sqrt 2 } \right)^2} + 10.{x^2}.{\left( { - \sqrt 2 } \right)^3} + 5.x.{\left( { - \sqrt 2 } \right)^4} + 1.{\left( { - \sqrt 2 } \right)^5}\\ = {x^5} - 5\sqrt 2 .{x^4} + 20{x^3} - 20\sqrt 2 .{x^2} + 20x - 4\sqrt 2 \end{array}\)
Đúng 0
Bình luận (0)
Tổng các hệ số nhị thức Niu – tơn trong khai triển (1+x)3n bằng 64. Số hạng không chứa x trong khai triển
2
n
x
+
1
2
n
x
2
3...
Đọc tiếp
Tổng các hệ số nhị thức Niu – tơn trong khai triển (1+x)3n bằng 64. Số hạng không chứa x trong khai triển 2 n x + 1 2 n x 2 3 n là:
A. 360
B. 210
C. 250
D. 240
Ta có: 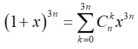
Chọn x=1. Ta có tổng hệ số bằng: ![]()
Lại có: 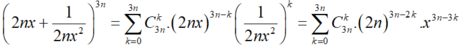
Số hạng không chứa x suy ra ![]()
Do đó số hạng không chứa x là: ![]()
Chọn D.
Đúng 0
Bình luận (0)
Tổng các hệ số nhị thức Niu – tơn trong khai triển
(
1
+
x
)
3
n
bằng 64. Số hạng không chứa x trong khai triển
(
2
n
x
+
1
2
n...
Đọc tiếp
Tổng các hệ số nhị thức Niu – tơn trong khai triển ( 1 + x ) 3 n bằng 64. Số hạng không chứa x trong khai triển ( 2 n x + 1 2 n x 2 ) 3 n là
A. 360
B. 210
C. 250
D. 240
Trongg khai triển nhị thức Newton của \({(2 + 3x)^4}\), hệ số của \({x^2}\) là:
A. 9
B. \(C_4^2\)
C. \(9C_4^2\)
D. \(36C_4^2\)
Ta có:
\({(2 + 3x)^4} = C_4^0{2^4} + C_4^1{2^3}3x + C_4^2{2^2}{\left( {3x} \right)^2} + C_4^32.{\left( {3x} \right)^3} + C_4^4{\left( {3x} \right)^4}\)
=> Hệ số của của \({x^2}\)là \(C_4^2{.2^2}{.3^2} = 36C_4^2.\)
Chọn D.
Đúng 0
Bình luận (0)
Hệ số của x8 trong khai triển nhị thức (x+ 1/x)20 là
Lời giải:
Theo khai triển Newton:
\((x+\frac{1}{x})^{20}=\sum\limits_{k=0}^{20}C^k_{20}x^k(x^{-1})^{20-k}=\sum\limits_{k=0}^{20}C^k_{20}x^{2k-20}\)
$2k-20=8\Leftrightarrow k=14$
Hệ số của $x^8$ là: $C^{14}_{20}$
Đúng 0
Bình luận (0)