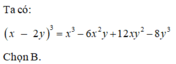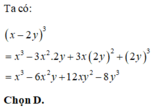Khai triển biểu thức x3-8x3

Những câu hỏi liên quan
Câu 1. Khai tiển biểu thức x3-8x3 ta được kết quả là:A. (x-2y)3 B. x3-2y3 C. (x-2y)(x2+2xy+4y2) D. x3-6x2y + 12xy2-8y3 Câu 2. Kết quả phép tính -x2(3-2x)là:A. 3x2-2x3 B.2x3-3x2 C.-3x3+2x2 D.-4x2 Câu 3. Để 4y2-12y +trở thành một hằng đảng thức. Giá trị trong ô vuông là:A. 6 B. 9 C. – 9 ...
Đọc tiếp
Câu 1. Khai tiển biểu thức x3-8x3 ta được kết quả là:
A. (x-2y)3 B. x3-2y3
C. (x-2y)(x2+2xy+4y2) D. x3-6x2y + 12xy2-8y3
Câu 2. Kết quả phép tính -x2(3-2x)là:
A. 3x2-2x3 B.2x3-3x2 C.-3x3+2x2
D.-4x2
Câu 3. Để 4y2-12y + trở thành một hằng đảng thức. Giá trị trong ô vuông là:
trở thành một hằng đảng thức. Giá trị trong ô vuông là:
A. 6 B. 9 C. – 9 D. Một kết quả khác
Câu 4. Biểu thức 1012 – 1 có giá trị bằng
A. 100 B. 1002 C. 102000 D. Một kết quả khác
Câu 5. Giá trị của biểu thức x2+2xy+y2 tại x = - 1 và y = - 3 bằng
A. 16 B. – 4 C. 8 D. Một kết quả khác
Câu 6. Biết 4x(x2-25)=0, các số x tìm được là:
A. 0; 4; 5 B. 0; 4 C. -5; 0; 5 D. Một kết quả khác
Câu 7.
A. -2x +4 =2(2-x) B. -2x+4 = -2(2-x)
C. -2x +4= -2(x+2) D. -2x+4= 2(x-2)
Câu 8. Thực hiện phép nhân x(x-y)
A.x2-y B.x-xy C.x-x2 D.x2-xy
Câu 1 : sửa x^3 - 8y^3
chọn C
Câu 2 : B
Đúng 1
Bình luận (0)
Câu 1.
\(x^2-8y^3=\left(x-2y\right)\left(x^2+2y+4y^2\right)\)
Câu 2.
\(-x^2\left(3-2x\right)=-3x^2+2x^3=2x^3-3x^2\)
Đúng 2
Bình luận (0)
Viết các biểu thức sau dưới dạng tích.
A)x3+27
B)x3-1/8
C)8x3+y3
D)8x3-27y3
A) \(x^3+27\)
\(=x^3+3^3\)
\(=\left(x+3\right)\left(x^2-3x+9\right)\)
B) \(x^3-\dfrac{1}{8}\)
\(=x^3-\left(\dfrac{1}{2}\right)^3\)
\(=\left(x-\dfrac{1}{2}\right)\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)\)
C) \(8x^3+y^3\)
\(=\left(2x\right)^3+y^3\)
\(=\left(2x+y\right)\left(4x^2-2xy+y^2\right)\)
D) \(8x^3-27y^3\)
\(=\left(2x\right)^3-\left(3y\right)^3\)
\(=\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)\)
Đúng 2
Bình luận (0)
a)\(\left(x+3\right)\left(x^2-3x+9\right)\)
b)\(\left(x-\dfrac{1}{2}\right)\left(x^2+\dfrac{1}{2}x+\dfrac{1}{4}\right)\)
c)\(\left(2x+y\right)\left(4x^2-2xy+y^2\right)\)
d)\(\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)\)
Đúng 0
Bình luận (0)
Chọn đáp án đúng nhất. Khai triển biểu thức 8x3-1 bằng:
A.(2x-1)3
B.(2x-1)(4x2+2x+1)
C.(8x-1)3
D.4x2-4x+1
Xem thêm câu trả lời
Chọn đáp án đúng nhất. Khai triển biểu thức 8x3-1 bằng:
A.(2x-1)3
B.(2x-1)(4x2+2x+1)
C.(8x-1)3
D.4x2-4x+1
Xem thêm câu trả lời
Khai triển biểu thức
x
–
2
y
3
ta được kết quả làA.
x
3
–
8
y
3
B.
x
3
–
2
y
3
C.
x
3...
Đọc tiếp
Khai triển biểu thức x – 2 y 3 ta được kết quả là
A. x 3 – 8 y 3
B. x 3 – 2 y 3
C. x 3 – 6 x 2 y + 6 x y 2 – 2 y 3
D. x 3 – 6 x 2 y + 12 x y 2 – 8 y 3
Tìm hệ số của x 3 trong khai triển của biểu thức: x + 2 x 2 6
+ Số hạng tổng quát của khai triển 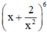 là:
là:
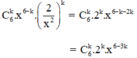
+ x3 ứng với 6 – 3k = 3 ⇔ k = 1.
Vậy hệ số của x3 là: 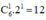
Đúng 0
Bình luận (0)
Khai triển biểu thức
(
x
-
2
y
)
3
ta được kết quả là:A.
x
3
-
8
y
3
B.
x
3
-
2
y
3
C.
x
3
−
6
x...
Đọc tiếp
Khai triển biểu thức ( x - 2 y ) 3 ta được kết quả là:
A. x 3 - 8 y 3
B. x 3 - 2 y 3
C. x 3 − 6 x 2 y + 6 x y 2 − 2 y 3
D. x 3 − 6 x 2 y + 12 x y 2 − 8 y 3
viết các biểu thức sau thành tích:
a, 8x3 - 1
b, x3 + 8y3
c, x3 + 125
d, x3 - 27y3
a: \(8x^3-1=\left(2x-1\right)\left(4x^2+2x+1\right)\)
b: \(x^3+8y^3=\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)
c: \(x^3+125=\left(x+5\right)\left(x^2-5x+25\right)\)
d: \(x^3-27y^3=\left(x-3y\right)\left(x^2+3xy+9y^2\right)\)
Đúng 1
Bình luận (0)
a) 8x3 - 1
= (2x)3 - 13
= (2x - 1)(4x2 + 2x + 1)
b) x3 + 8y3
= x3 + (2y)3
= (x + 2y)(x2 + 2xy + 4y2)
c) x3 + 125
= x3 + 53
= (x + 5)(x2 - 5x + 25)
d) x3 - 27y3
= x3 - (3y)3
= (x - 3y)(x2 + 3xy + 9y2)
Chúc bạn học tốt
Đúng 1
Bình luận (0)
a. 8x3 - 1
⇔ (2x)3 - 13
⇔ (2x - 1)3.
b. x3 + 8y3
⇔ x3 + (2y)3
⇔ (x + 2y)3
c. x3 + 125
⇔ x3 + 53
⇔ (x + 5)3
d. x3 - 27y3
⇔ x3 - (3y)3
⇔ (x - 3y)3
Đúng 0
Bình luận (0)
Tìm số hạng không chứa x trong khai triển thành đa thức của biểu thức
x
3
+
1
x
4
7
,
x
0.
A.
C
7
6
. B.
C
7...
Đọc tiếp
Tìm số hạng không chứa x trong khai triển thành đa thức của biểu thức x 3 + 1 x 4 7 , x > 0.
A. C 7 6 .
B. C 7 2 .
C. C 7 5
D. C 7 4 .
Đáp án D
Ta có
x 3 + 1 x 4 7 = x 1 3 + x − 1 4 7 = k = 0 7 C 7 k x 1 3 7 − k x − 1 4 k = k = 0 7 C 7 k x 7 3 − 7 k 12
Số hạng không chứa x tương ứng với số hạng chứa k thỏa mãn
7 3 − 7 k 12 = 0 ⇔ k = 4 .
Vậy số hạng không chứa x là C 7 4 .
Đúng 0
Bình luận (0)
Hệ số của số hạng chứa
x
3
trong khai triển thành đa thức của biểu thức
A
1
−
x
10
là A. 30 B. -120 C. 120 D. -30
Đọc tiếp
Hệ số của số hạng chứa x 3 trong khai triển thành đa thức của biểu thức A = 1 − x 10 là
A. 30
B. -120
C. 120
D. -30