Giải phương trình nghiệm nguyên
a, x2-2xy+5y2 = y +1
b,x6+3x3+1=y4
Phân tích các đa thức sau thành nhân tử:
a) x8 + x4 + 1
b) x12 - 3x6 - 1
c) 3x4 + 10x2 - 25
d) x2 - 5y2 - y4 + 2xy - 9
Lời giải:
a.
$x^8+x^4+1=(x^4)^2+2x^4+1-x^4$
$=(x^4+1)^2-(x^2)^2=(x^4+1-x^2)(x^4+1+x^2)$
$=(x^4+1-x^2)[(x^2+1)^2-x^2]$
$=(x^4-x^2+1)(x^2+1-x)(x^2+1+x)$
b.
$x^{12}-3x^6-1=(x^6-\frac{3}{2})^2-\frac{13}{4}$
$=(x^6-\frac{3}{2}-\frac{\sqrt{13}}{2})(x^6-\frac{3}{2}+\frac{\sqrt{13}}{2})$
c.
$3x^4+10x^2-25=(3x^4+15x^2)-(5x^2+25)$
$=3x^2(x^2+5)-5(x^2+5)=(x^2+5)(3x^2-5)$
$=(x^2+5)(\sqrt{3}x-\sqrt{5})(\sqrt{3}x+\sqrt{5})$
c.
$x^2-5y^2-y^4+2xy-9$
$=(x^2+2xy+y^2)-(y^4+6y^2+9)$
$=(x+y)^2-(y^2+3)^2$
$=(x+y+y^2+3)(x+y-y^2-3)$
\(a,x^8+x^4+1\\ =\left(x^8+2x^4+1\right)-x^4\\ =\left(x^4+1\right)^2-x^4\\ =\left(x^4-x^2+1\right)\left(x^4+x^2+1\right)\\ b,x^{12}-3x^6-1\\ =\left(x^{12}-2x^6+1\right)-x^6-2\\ =\left(x^6-1\right)^2-x^6-2\\ =\left(x^6-x^3-1\right)\left(x^6+x^3-1\right)-2???\\ c,3x^4+10x^2-25\\ =4x^4-\left(x^4-10x^2+25\right)\\ =4x^4-\left(x^2-5\right)^2\\ =\left(2x^2-x^2+5\right)\left(2x^2+x^2-5\right)\\ =\left(x^2+5\right)\left(3x^2-5\right)\\ d,x^2-5y^2-y^4+2xy-9\\ =\left(x^2+2xy+y^2\right)-\left(y^4+6y^2+9\right)\\ =\left(x+y\right)^2-\left(y^2+3\right)^2\\ =\left(x+y+y^2+3\right)\left(x+y-y^2-3\right)\)
a) x8+x4+1 = (x4+1)2-x4 = (x4-x2+1)(x4+x2+1)
b) x12-3x6-1 = (x6-1)2-x6 = (x6-x3-1)(x6+x3-1)
c) 3x4+10x2-25 = 4x4-(x4-10x2+25) = 4x4- (x2-5)2 = (x2+5)(3x2-5)
d) x2-5y2-y4+2xy-9 = (x+y)2-(y2+3)2 = (x+y-y2-3)(x+y+y2+3)
Cho số thực x, y thỏa mãn x 2 + y 2 + x y = 4 y − 1 + 3 x . Tìm giá trị lớn nhất của biểu thức P = 3 x 3 − y 3 + 20 x 2 + 2 x y + 5 y 2 + 39 x
A. 120 2
B. 110
C. 100
D. 96 3
Đáp án C
G T ⇔ x 2 + y − 3 x + y 2 − 4 y + 4 = 0 y 2 + x − 4 y + x 2 − 3 x + 4 = 0
có nghiệm ⇔ Δ x ≥ 0 Δ y ≥ 0 ⇔ 0 ≤ x ≤ 4 3 1 ≤ y ≤ 7 3
Và:
x y = 3 x + 4 y − x 2 − y 2 − 4 ⇒ P = 3 x 3 + 18 x 2 + 45 x − 8 ⏟ f x + − 3 y 3 + 3 y 2 + 8 y ⏟ g y
Xét hàm số f x = 3 x 3 + 18 x 2 + 45 x − 8 trên 0 ; 4 3 ⇒ max 0 ; 4 3 f x = f 4 3 = 820 9
Xét hàm số g x = − 3 y 3 + 3 y 2 + 8 y trên 1 ; 7 3 ⇒ max 1 ; 7 3 g x = f 4 3 = 80 9
Vật P ≤ max 0 ; 4 3 f x + max 1 ; 7 3 g x = 100
Dấu “=” xảy ra khi x = y = 4 3
Giải phương trình nghiệm nguyên: 2x3+2x2y+x2+2xy=x+10
a) Tìm số nguyên âm x để đa thức:
f(x)= -x4+2x2-3x+5 chia hết cho g(x)= x-1
b) Tìm giá trị nhỏ nhất của biểu thức:
B= x2+5y2-2xy+4x-4y-2020
\(a,f\left(x\right)⋮g\left(x\right)\\ \Leftrightarrow\dfrac{-x^4+2x^2-3x+5}{x-1}\in Z\\ \Leftrightarrow\dfrac{-x^4+x^3-x^3+x^2+x^2-x-2x+2+3}{x-1}\in Z\\ \Leftrightarrow\dfrac{-x^3\left(x-1\right)-x^2\left(x-1\right)+x\left(x-1\right)-2\left(x-1\right)+3}{x-1}\in Z\\ \Leftrightarrow-x^3-x^2+x-2+\dfrac{3}{x-1}\in Z\\ \Leftrightarrow3⋮x-1\\ \Leftrightarrow x-1\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow x\in\left\{-2;0;2;4\right\}\\ Mà.x< 0\\ \Leftrightarrow x=-2\\ b,B=\left(x^2-2xy+y^2\right)+4\left(x-y\right)+4+4y^2-2024\\ B=\left(x-y\right)^2+4\left(x-y\right)+4+4y^2-2024\\ B=\left(x-y-2\right)^2+4y^2-2024\ge-2024\\ B_{min}=-2024\Leftrightarrow\left\{{}\begin{matrix}x=y+2\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
1/ số nghiệm của phương trình ( x - 1 ) ( x + 7 ) ( x - 5 ) = 0 là
A. 0
B. 1
C. 2
D. 3
2/ số nghiệm của phương trình ( x2 - 1 ) ( x2 + 7 ) ( x2 - 4 ) = 0 là
A. 1
B. 2
C. 3
D. 4
3/ số nghiệm của phương trình ( x3 - 1 ) ( x2 + 9 ) ( x2 + x + 1 ) = 0 LÀ
A. 1
B.2
C.3
D.4
4/ số nghiệm của phương trình ( x3 - 8 ) ( x2 + 9 ) ( x2 - x + 1 ) = 0 là
A. 1
B. 2
C. 3
D. 4
Bài 1 : tìm x ; y nguyên dương
2xy + x + y = 83
Bài 2 tìm nghiệm nguyên của phương trình :
a ) x2 + 2y2 + 3xy - x - y + 3 = 0
b ) 6x2y3 + 3x2 - 10y3 = -2
bài 1
Ta có 2xy+x+y=83
<=>4xy+2x+2y=166
2x*(2y+1)+(2y+1)=167
(2x+1)*(2y+1)=167
=>2x+1;2y+1 thuộc Ư(167)
do x,y nguyên dương =>2TH
TH1 2x+1=1;2y+1=167=>x=...;y=....
TH2 2x+1=167;2y+1=1=>x=...;y=....
Tìm GTNN hoặc GTLN của các biểu thức sau:
a) 2x2 - x + 1
b) 5x - x2 + 4
c) x2 + 5y2 - 2xy + 4y + 3
a) \(2x^2-x+1=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{7}{8}\ge\dfrac{7}{8}\)
\(ĐTXR\Leftrightarrow x=\dfrac{1}{4}\)
b) \(5x-x^2+4=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\)
\(ĐTXR\Leftrightarrow x=\dfrac{5}{2}\)
c) \(x^2+5y^2-2xy+4y+3=\left(x-y\right)^2+\left(2y+1\right)^2+2\ge2\)
\(ĐTXR\Leftrightarrow\)\(x=y=-\dfrac{1}{2}\)
b: ta có: \(-x^2+5x+4\)
\(=-\left(x^2-5x-4\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}-\dfrac{41}{4}\right)\)
\(=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{41}{4}\le\dfrac{41}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{5}{2}\)
Không cần vẽ hình, hãy cho biết số nghiệm của mỗi hệ phương trình sau đây và giải thích vì sao:
a ) y = 3 − 2 x y = 3 x − 1 b ) y = − 1 2 x + 3 y = − 1 2 x + 1 c ) 2 y = − 3 x 3 y = 2 x d ) 3 x − y = 3 x − 1 3 y = 1
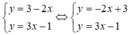
a) Xét (d): y = -2x + 3 có a = -2; b = 3
(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.
Có a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 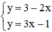 có nghiệm duy nhất.
có nghiệm duy nhất.
b) 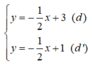
Xét (d): 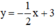 có a =
có a = 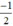 ; b = 3
; b = 3
(d’): 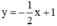 có a’ =
có a’ = 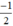 ; b’ = 1.
; b’ = 1.
Có a = a’; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ phương trình 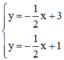 vô nghiệm.
vô nghiệm.
c) Ta có: 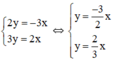
Xét (d): y = 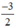 x có a =
x có a = 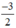 ; b = 0
; b = 0
(d’) : y = 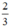 x có a’ =
x có a’ = 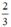 ; b’ = 0
; b’ = 0
Ta có: a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 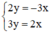 có nghiệm duy nhất.
có nghiệm duy nhất.
d) Ta có:
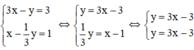
Ta có: a = a’=3; b = b’ = -3
Nhận thấy hai đường thẳng trên trùng nhau
⇒ Hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 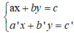
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.
Bài 2: Cho phương trình x2-2mx+2m-2=0 (1) (m là tham số)
a) Giải phương trình (1) khi m=1
b) Chứng minh phương trình (1) luôn có 2 nghiệm x1,x2. Tìm m để x12 +x22 =12
a) Với m=1,ta có:
x2-2.1.x+2.1-2=0
<=> x2-2x=0
<=> x(x-2)=0
<=> x=0 hoặc x-2=0
<=> x=0 hoặc x=2
Giải hệ phương trình:
phương trình 1:x2-5y2-8y=3
phương trình 2:(2x+4y-1)√(2x-y-1)=(4x-2y-3)√(x+2y)