a:

\(\text{Δ}=\left(m-1\right)^2-4\left(-2m-1\right)\)

\(=m^2-2m+1+8m+4=m^2+6m+5\)

Để (1) vô nghiệm thì (m+1)(m+5)<0

hay -5<m<-1

Để (1) có nghiệm thì (m+1)(m+5)>=0

=>m>=-1 hoặc m<=-5 

Để (1) có hai nghiệm phân biệt thì (m+1)(m+5)>0

=>m>-1 hoặc m<-5

b: Để (1) có hai nghiệm phân biệt cùng dương thì

\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>-1\\m< -5\end{matrix}\right.\\m>1\\m< -\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

c. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-2m-1\end{matrix}\right.\)

\(x_1^2+x_2^2=3\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\)

\(\Leftrightarrow\left(m-1\right)^2+2\left(2m+1\right)=3\)

\(\Leftrightarrow m^2+2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-2\left(loại\right)\end{matrix}\right.\)

Đáp án C

Xét y = 2x³ – 3x² + 1 

Ta có: y’ = 6x² – 6x

ð y’ = 0 ⇔ x = 0 hoặc x = 1

Ta có bảng biến thiên

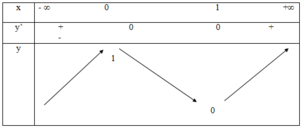
Số nghiệm phương trình đã cho m = 2x³ – 3x² + 1 

= Số giao điểm của đồ thị hàm số y = 2x³ – 3x² + 1 và đường thẳng y = m

-> 0<m<1

\(x^3-x^2+2mx-2m=0\)

\(\Leftrightarrow x^2\left(x-1\right)+2m\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2+2m\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2=-2m\end{matrix}\right.\)

Để pt có 3 nghiệm \(\Rightarrow-2m>0\Rightarrow m< 0\)

a. Do vai trò 3 nghiệm như nhau, ko mất tính tổng quát giả sử \(x_1=1\) và \(x_2;x_3\) là nghiệm của \(x^2+2m=0\) 

Để pt có 3 nghiệm pb \(\Rightarrow\left\{{}\begin{matrix}-2m>0\\-2m\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< 0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\)

Khi đó: \(x_2+x_3=0\Rightarrow x_1+x_2+x_3=1\ne10\) với mọi m

\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu

b.

Giả sử pt có 3 nghiệm, khi đó \(\left[{}\begin{matrix}x_2=-\sqrt{-2m}< 0< 1\\x_3=\sqrt{-2m}\end{matrix}\right.\)

\(\Rightarrow\) Luôn có 1 nghiệm của pt âm \(\Rightarrow\) không tồn tại m thỏa mãn

Em coi lại đề bài

còn cái nịt

a) \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\\ =m^2+6m+9-4m\\ =m^2+2m+9\\ =\left(m+1\right)^2+8>0\forall m\)

Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m.

b) Áp dụng hệ thức Vi-et, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1x_2=m\end{matrix}\right.\)

Mà \(x_1^2+x_2^2=6\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\\ \Leftrightarrow\left(m+3\right)^2-2m=6\\ \Leftrightarrow m^2+6m+9-2m=6\\ \Leftrightarrow m^2+4m+3=0\\ \Leftrightarrow\left(m+1\right)\left(m+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)

Vậy \(m\in\left\{-1;-3\right\}\) là các giá trị cần tìm.

a, Ta có: \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\)

                   \(=m^2+6m+9-4m\)

                   \(=m^2+2m+9\)

                   \(=m^2+2m+1+8\)

                   \(=\left(m+1\right)^2+8\)

Lại có:  \(\left(m+1\right)^2\ge0\forall m\Rightarrow\left(m+1\right)^2+8\ge8\forall m\)

Vậy phương trình luôn có 2 nghiêm phân biệt 

b, Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1+x_2=m\end{matrix}\right.\)

Theo bài ra:

 \(x_1^2+x_2^2=6\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)

\(\Leftrightarrow\left(m+3\right)^2-2m=6\)

\(\Leftrightarrow m^2+6m+9-2m=6\)

\(\Leftrightarrow m^2+6m+9-2m-6=0\)

\(\Leftrightarrow m^2+4m+3=0\)

\(\Leftrightarrow m^2+m+3m+3=0\)

\(\Leftrightarrow\left(m^2+m\right)+\left(3m+3\right)=0\)

\(\Leftrightarrow m\left(m+1\right)+3\left(m+1\right)=0\)

\(\Leftrightarrow\left(m+1\right)\left(m+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}m+1=0\\m+3=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)

Vậy với m=-1 hoặc m=-3 thì phương trinh trên thỏa mãn hệ thức 

\(\Delta=\left(m+3\right)^2-4\left(m-1\right)=\left(m+1\right)^2+12>0;\forall m\)

\(\Rightarrow\) Pt luôn có 2 nghiệm pb

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1x_2=m-1\end{matrix}\right.\)

\(x_1< -\dfrac{1}{4}< x_2\Leftrightarrow\left(x_1+\dfrac{1}{4}\right)\left(x_2+\dfrac{1}{4}\right)< 0\)

\(\Leftrightarrow x_1x_2+\dfrac{1}{4}\left(x_1+x_2\right)+\dfrac{1}{16}< 0\)

\(\Leftrightarrow m-1+\dfrac{1}{4}\left(m+3\right)+\dfrac{1}{16}< 0\)

\(\Leftrightarrow20m-3< 0\Rightarrow m< \dfrac{3}{20}\)

\(x^3-3\left(m+1\right)x^2+2mx+m+2=0\left(1\right)\)

\(\Leftrightarrow\left(x-1\right)\left(x^2-3mx-2x-m-2\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left[x^2-x\left(3m+2\right)-m-2\right]=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2-x\left(3m+2\right)-m-2=0\left(2\right)\end{matrix}\right.\)

\(\left(1\right)có\) \(3ngo\)  \(phân\) \(biệt\Leftrightarrow\left(2\right)\) \(có\) \(2\) \(ngo\) \(phân\) \(biệt\ne1\)

\(\Leftrightarrow\left\{{}\begin{matrix}g\left(1\right)\ne0\\\Delta>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{-3}{4}\\\left(3m+2\right)^2-4\left(-m-2\right)>0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{-3}{4}\\9m^2+16m+12>0\left(luôn-đúng\right)\end{matrix}\right.\)

\(\Rightarrow m\ne\dfrac{-3}{4}\) \(thì\left(1\right)\) \(có\) \(3ngo\) \(phân\) \(biệt\)

\(do\left(2\right)\) \(\) \(có\) \(2\) \(ngo\) \(phân\) \(biệt\ne1\Rightarrow x3=1\)

\(\Rightarrow x1+x2=2\)

\(vi-ét\Rightarrow\left\{{}\begin{matrix}x1+x2=3m+2\\x1x2=-m-2\end{matrix}\right.\)

\(\Rightarrow3m+2=2\Leftrightarrow m=0\left(tm\right)\)