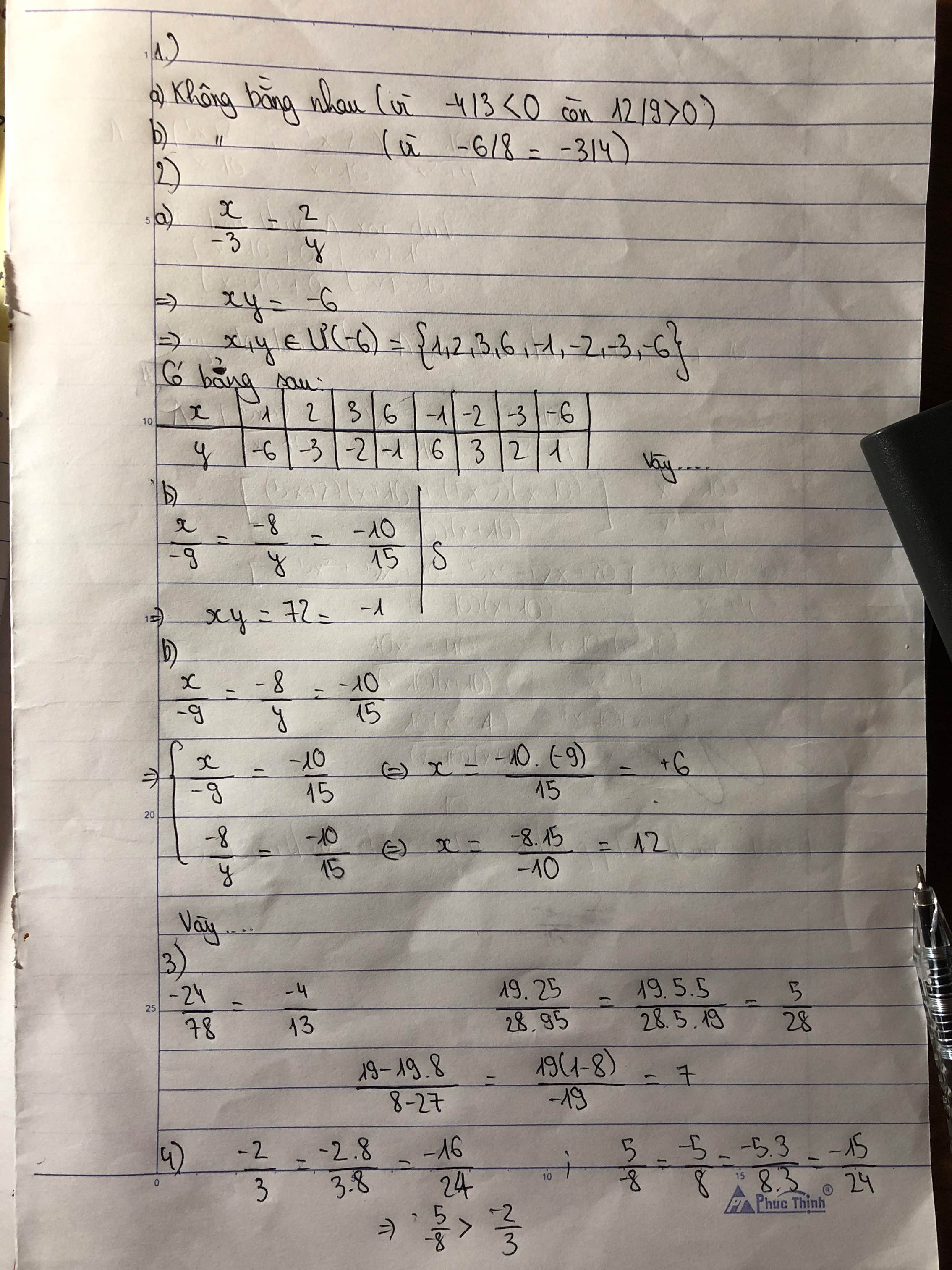so sánh
A=1^2+3^2+..+21^2
B=2^2+4^2+...+20^2

Những câu hỏi liên quan
Bài 5: So sánh
a) 2^6 & 8^2
b) 5^3 & 3^5
a) \(2^6\) và \(8^2\)
\(2^6=\left(2^2\right)^3\)
\(8^2=\left(2^3\right)^2\)\(=2^6\)
\(\Rightarrow\) \(2^6=8^2\)
Đúng 0
Bình luận (0)
Bài 4: So sánh
a) -2/3 và 5/-8
b) 398/-412 và -25/-137
c) -14/21 và 60/72
a)
\(\dfrac{-2}{3}\)>\(\dfrac{5}{-8}\)
b)
\(\dfrac{398}{-412}\)<\(\dfrac{-25}{-137}\)
c)
\(\dfrac{-14}{21}\)<\(\dfrac{60}{72}\)
Đúng 0
Bình luận (0)
bài 20 : tìm x dfrac{1}{1.2}+dfrac{1}{2.3}+...+ dfrac{1}{x.left(x+1right)}+dfrac{1}{2018.2019}bài 21: tìm xdfrac{x+1}{99}+dfrac{x+2}{98}+dfrac{x+3}{97}+dfrac{x+4}{96}-4bài 22: so sánha) dfrac{-1}{5}+dfrac{4}{-5} và 1b) dfrac{3}{5} và dfrac{2}{3}+dfrac{-1}{5}c) dfrac{3}{2}+dfrac{-4}{3} và dfrac{1}{10}+dfrac{-4}{5}d)dfrac{1}{2}+dfrac{1}{3}+dfrac{1}{4}+dfrac{1}{5}+dfrac{1}{6} và 2
Đọc tiếp
bài 20 : tìm x
\(\dfrac{1}{1.2}\)+\(\dfrac{1}{2.3}\)+...+ \(\dfrac{1}{x.\left(x+1\right)}\)+\(\dfrac{1}{2018.2019}\)
bài 21: tìm x
\(\dfrac{x+1}{99}\)+\(\dfrac{x+2}{98}\)+\(\dfrac{x+3}{97}\)+\(\dfrac{x+4}{96}\)=-4
bài 22: so sánh
a) \(\dfrac{-1}{5}\)+\(\dfrac{4}{-5}\) và 1
b) \(\dfrac{3}{5}\) và \(\dfrac{2}{3}\)+\(\dfrac{-1}{5}\)
c) \(\dfrac{3}{2}\)+\(\dfrac{-4}{3}\) và \(\dfrac{1}{10}\)+\(\dfrac{-4}{5}\)
d)\(\dfrac{1}{2}\)+\(\dfrac{1}{3}\)+\(\dfrac{1}{4}\)+\(\dfrac{1}{5}\)+\(\dfrac{1}{6}\) và 2
Bài 21:
Ta có: \(\dfrac{x+1}{99}+\dfrac{x+2}{98}+\dfrac{x+3}{97}+\dfrac{x+4}{96}=-4\)
\(\Leftrightarrow\dfrac{x+1}{99}+1+\dfrac{x+2}{98}+1+\dfrac{x+3}{97}+1+\dfrac{x+4}{96}+1=0\)
\(\Leftrightarrow\dfrac{x+100}{99}+\dfrac{x+100}{98}+\dfrac{x+100}{97}+\dfrac{x+100}{96}=0\)
\(\Leftrightarrow\left(x+100\right)\left(\dfrac{1}{99}+\dfrac{1}{98}+\dfrac{1}{97}+\dfrac{1}{96}\right)=0\)
mà \(\dfrac{1}{99}+\dfrac{1}{98}+\dfrac{1}{97}+\dfrac{1}{96}>0\)
nên x+100=0
hay x=-100
Vậy: x=-100
Đúng 0
Bình luận (0)
cho m>n hãy so sánh
a)2m-2 vs 2n-2
b)1-3m vs 1-3n
c)2m+3 vs 2n+1
d)3-5m vs 7-5n
a: m>n
=>2m>2n
=>2m-2>2n-2
b: m>n
=>-3m<-3n
=>-3m+1<-3n+1
c: m>n
=>2m>2n
=>2m+3>2n+3
mà 2n+3>2n+1
nên 2m+3>2n+1
d: m>n
=>-5m<-5n
=>-5m+3<-5n+3
mà -5n+3<-5n+7
nên -5m+3<-5n+7
Đúng 0
Bình luận (0)
Bài 4: So sánh
a) -2/3 và 5/-8
b) 398/-412 và -25/-137
c) -14/21 và 60/72
giải chi tiết
Bài 1: Cặp phân số sau có bằng nhau không?a) -4/3 và 12/9b) -2/3 và -6/8Bài 2: Tìm x,y biếta)x/-32/yb) x/-9-8/y-10/15Bài 3: Rút gọna) -24/78b)19.25/28.95c) 19-19.8/8-27Bài 4: So sánha) -2/3 và 5/-8b) 398/-412 và -25/-137c) -14/21 và 60/72Bài 5: a) Cho A 5/n-3 Tìm điều kiện của n để A là phân sốb) Cho B 2n+7/n+3Tìm giá trị của n để B là sô nguyên
Đọc tiếp
Bài 1: Cặp phân số sau có bằng nhau không?
a) -4/3 và 12/9
b) -2/3 và -6/8
Bài 2: Tìm x,y biết
a)x/-3=2/y
b) x/-9=-8/y=-10/15
Bài 3: Rút gọn
a) -24/78
b)19.25/28.95
c) 19-19.8/8-27
Bài 4: So sánh
a) -2/3 và 5/-8
b) 398/-412 và -25/-137
c) -14/21 và 60/72
Bài 5: a) Cho A= 5/n-3 Tìm điều kiện của n để A là phân số
b) Cho B= 2n+7/n+3
Tìm giá trị của n để B là sô nguyên
1:
a: Vì \(\dfrac{-4}{3}=\dfrac{-4\cdot3}{3\cdot3}=\dfrac{-12}{9}=\dfrac{12}{9}\\ \Rightarrow\dfrac{-4}{3}=\dfrac{12}{9}\)
b: Vì : \(-2\cdot3=-6\\ -6\cdot8=-48\)
nên 2 p/s ko bằng nhau
Đúng 1
Bình luận (1)
so sánh
a 3+ căn 5 và 2 căn 2 + căn 6
b 3 / căn 7 -2 - 4/căn 7 + căn 3
b: \(\dfrac{3}{\sqrt{7}-2}-\dfrac{4}{\sqrt{7}+\sqrt{3}}\)
\(=\sqrt{7}+2-\sqrt{7}+\sqrt{3}=2+\sqrt{3}\)
Đúng 0
Bình luận (0)
So sánha.2sqrt{29} và 3sqrt{13}b.dfrac{5}{4}sqrt{2} và dfrac{3}{2}sqrt{dfrac{3}{2}}c.5sqrt{2} và 4sqrt{3}d.dfrac{5}{2}sqrt{dfrac{1}{6}} và 6sqrt{dfrac{1}{37}}
Đọc tiếp
So sánh
a.2\(\sqrt{29}\) và 3\(\sqrt{13}\)
b.\(\dfrac{5}{4}\)\(\sqrt{2}\) và \(\dfrac{3}{2}\)\(\sqrt{\dfrac{3}{2}}\)
c.5\(\sqrt{2}\) và 4\(\sqrt{3}\)
d.\(\dfrac{5}{2}\sqrt{\dfrac{1}{6}}\) và 6\(\sqrt{\dfrac{1}{37}}\)
a)
Có:
\(2\sqrt{29}=\sqrt{4.29}=\sqrt{116}\\ 3\sqrt{13}=\sqrt{9.13}=\sqrt{117}\)
Vì \(\sqrt{117}>\sqrt{116}\) nên \(3\sqrt{13}>2\sqrt{29}\)
b)
Có:
\(\dfrac{5}{4}\sqrt{2}=\sqrt{\dfrac{25}{16}.2}=\sqrt{\dfrac{25}{8}}\)
\(\dfrac{3}{2}\sqrt{\dfrac{3}{2}}=\sqrt{\dfrac{9}{4}.\dfrac{3}{2}}=\sqrt{\dfrac{27}{8}}\)
Do \(\sqrt{\dfrac{27}{8}}>\sqrt{\dfrac{25}{8}}\) nên \(\dfrac{3}{2}\sqrt{\dfrac{3}{2}}>\dfrac{5}{4}\sqrt{2}\)
c)
Có:
\(5\sqrt{2}=\sqrt{25.2}=\sqrt{50}\)
\(4\sqrt{3}=\sqrt{16.3}=\sqrt{48}\)
Vì \(\sqrt{50}>\sqrt{48}\) nên \(5\sqrt{2}>4\sqrt{3}\)
d)
Có:
\(\dfrac{5}{2}\sqrt{\dfrac{1}{6}}=\sqrt{\dfrac{25}{4}.\dfrac{1}{6}}=\sqrt{\dfrac{25}{24}}\)
\(6\sqrt{\dfrac{1}{37}}=\sqrt{36.\dfrac{1}{37}}=\sqrt{\dfrac{36}{37}}\)
lại có: \(\dfrac{25}{24}>\dfrac{36}{37}\)
\(\Rightarrow\dfrac{5}{2}\sqrt{\dfrac{1}{6}}>6\sqrt{\dfrac{1}{37}}\)
Đúng 2
Bình luận (0)
CHO A=1+2+2^2+2^3+..+2^9;B=5.2^8.SO SÁNHA VÀ B
A=1+2+2^2+2^3+....+2^9
2A=2+2^2+2^3+....+2^10
2A-A=2^10-1
A=2^10-1/2
B=5.2^8=(2^2+1).2^8=2^10+2^8
=>B>A
Đúng 0
Bình luận (0)
2A = 2(1 + 2 + 22 + .... + 29 )
= 2 + 22 + 23 + ..... + 210
2A - A = (2 + 22 + 23 + ..... + 210) - (1 + 2 + 22 + .... + 29 )
A = 210 - 1
B = 5.28 = (22 + 1).28 = 210 + 28
210 - 1 < 210 + 28
=> A < B
Đúng 0
Bình luận (0)
so sánh
A = \(\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}...\dfrac{99}{100}\)và \(B=\dfrac{1}{10}\)