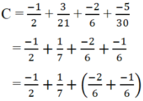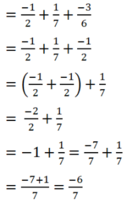(59-530) - (59 +33 + 530)

Những câu hỏi liên quan
a, A = 1 + 2 + 22 + 23 + ... + 250 =
b, B = 1 + 3 + 32 + 33 + ... 3100 =
c, C = 5 + 52 + 53 + ... 530 =
d, D = 2100 = 299 + 298 - 297 + ... + 22 - 2
a) \(A=1+2+2^2+...+2^{50}\)
\(\Rightarrow2A=2+2^2+...+2^{51}\)
\(\Rightarrow A=2A-A=2+2^2+...+2^{51}-1-2-2^2-...-2^{50}=2^{51}-1\)
b) \(B=1+3+3^2+...+3^{100}\)
\(\Rightarrow3B=3+3^2+...+3^{101}\)
\(\Rightarrow2B=3B-B=3+3^2+...+3^{101}-1-3-3^2-...-3^{100}=3^{101}-1\)
\(\Rightarrow B=\dfrac{3^{101}-1}{2}\)
c) \(C=5+5^2+...+5^{30}\)
\(\Rightarrow5C=5^2+5^3+...+5^{31}\)
\(\Rightarrow4C=5C-C=5^2+5^3+...+5^{31}-5-5^2-...-5^{30}=5^{31}-5\)
\(\Rightarrow C=\dfrac{5^{31}-5}{4}\)
d) \(D=2^{100}-2^{99}+2^{98}-...+2^2-2\)
\(\Rightarrow2D=2^{101}-2^{100}+2^{99}-...+2^3-2^2\)
\(\Rightarrow3D=2D+D=2^{101}-2^{100}+2^{99}-...+2^3-2^2+2^{100}-2^{99}+...+2^2-2=2^{101}-2\)
\(\Rightarrow D=\dfrac{2^{101}-2}{3}\)
Đúng 0
Bình luận (0)
Câu 39. Nếu hình bình hành ABCD có góc A 530 thìA.Góc D 530 B. Góc B Góc C 530. C. Góc C 1270 D. Góc D 1270 Câu 40. Hai cạnh kề của hình bình hành tỉ lệ với 1 và 2 và chu vi của hình bình hành bằng 30cm. Khi đó độ dài hai cạnh kề của hình bình hành làA. 12cm và 18cm B. 5cm và 10cm C. 15cm và 30cm D. 9cm và 18cm
Đọc tiếp
Câu 39. Nếu hình bình hành ABCD có góc A = 530 thì
A.Góc D= 530 B. Góc B= Góc C = 530.
C. Góc C= 1270 D. Góc D= 1270
Câu 40. Hai cạnh kề của hình bình hành tỉ lệ với 1 và 2 và chu vi của hình bình hành bằng 30cm. Khi đó độ dài hai cạnh kề của hình bình hành là
A. 12cm và 18cm B. 5cm và 10cm
C. 15cm và 30cm D. 9cm và 18cm
Xem thêm câu trả lời
Cho các số sau:53 460 54 360 46 530 53 640a) Chọn câu trả lời đúng.Trong các số đã cho:- Số lớn nhất là:A. 53 460 B. 54 360 C. 46 530 D. 53 640- Số bé nhất là:A. 53 460 B. 54 360 C. 46 530 D. 53 640b) – Viết các số đã cho theo thứ tự từ bé đến lớn.– Viết các số đã cho theo thứ tự từ lớn đến bé.
Đọc tiếp
Cho các số sau:
53 460 54 360 46 530 53 640
a) Chọn câu trả lời đúng.Trong các số đã cho:
- Số lớn nhất là:
A. 53 460 B. 54 360 C. 46 530 D. 53 640
- Số bé nhất là:
A. 53 460 B. 54 360 C. 46 530 D. 53 640
b) – Viết các số đã cho theo thứ tự từ bé đến lớn.
– Viết các số đã cho theo thứ tự từ lớn đến bé.
a) Trong các số đã cho:
b) – Các số đã cho theo thứ tự từ bé đến lớn: 46 530; 53 460; 53 640; 54 360.
– Các số đã cho theo thứ tự từ lớn đến bé: 54 360; 53 640; 53 460; 46 530.
Đúng 2
Bình luận (0)
430+(145-x)=530
45-(88-530)= ?
0,(530+0,46)
x + 20 = 530 + 50
x + 20 = 530 + 50
x+ 20 = 580
x = 580 - 20
x = 560
Đúng 0
Bình luận (0)
x + 20 = 530 + 50
x + 20 = 580
x = 580 - 20
x = 560
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính nhanh:
C = - 1 2 + 3 21 + - 2 6 + - 5 30
A = 71 . 52 + 52 / 530 . 71 - 180
A = 71 . 52 + 52 / 530 . 71 - 180
A = 3692 + 52 / 37630 - 180
A = 3744 / 37450
Vậy :...
Đúng 0
Bình luận (0)
Tính giá trị \(B=2\frac{1}{33}\times\frac{1}{59}-\frac{1}{11}\times3\frac{58}{59}-\frac{4}{33\times59}+\frac{4}{11}\)
Đặt \(a=\frac{1}{33}\), \(b=\frac{1}{59}\)
Có B= \(\left(2+\frac{1}{33}\right).\frac{1}{59}-3.\frac{1}{33}.\left(3+\frac{58}{59}\right)-4.\frac{1}{33}\frac{1}{59}+4.\frac{1}{33}.3\)
= \(\left(2+a\right)b-3a\left(3+1-\frac{1}{59}\right)-4ab+4.a.3\)
= \(2b+ab-3a\left(4-b\right)-4ab+12a\)
= \(2b+ab-12a+3ab-4ab+12a\)
= \(2b=\frac{2}{59}\)
Vậy B= \(\frac{2}{59}\)
Đúng 0
Bình luận (0)