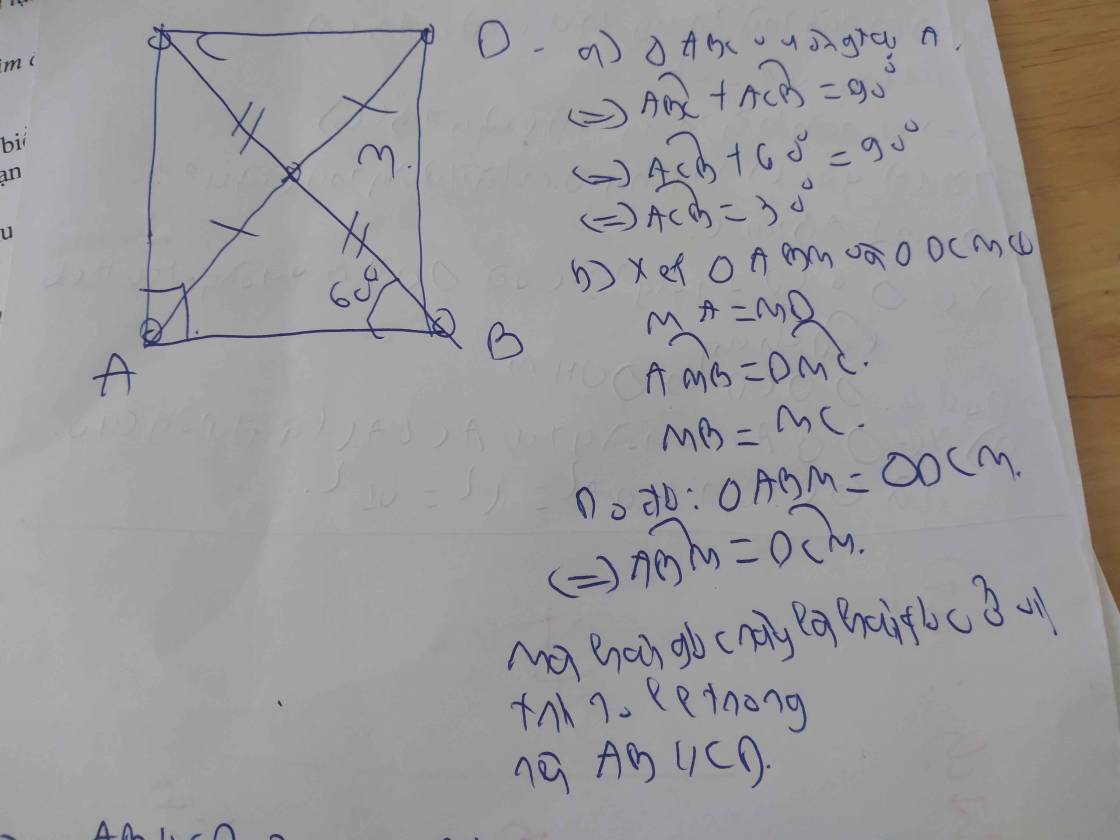
cho hình 60, trong đó ABM = 30o, MOC = 60o. BM DM. Chứng tỏ rằng AB // CD

Những câu hỏi liên quan
cho tam giác ABC vuông tại A có góc B bằng 60 độ. Gọi M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho DM=MA
a)Tính góc ACB
b)Chứng minh: Tam giác ABM=tam giác DCM và AB//CD
c)Chứng minh: AM=1/2 BC
Cho tam giác ABC có ABC=60 độ và ACB= 30 độ. Gọi M là trung điểm của BC. Chứng tỏ rằng tam giác ABM đều và AB = 1/2 BC
Ta có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\Rightarrow\widehat{BAC}=180^0-60^0-30^0=90^0\)
Do đó tam giác ABC vuông tại A
Trên tia đối MA lấy D sao cho M là trung điểm AD
\(\left\{{}\begin{matrix}CM=MB\\AM=MD\\\widehat{CMA}=\widehat{BMD}\left(đối.đỉnh\right)\end{matrix}\right.\Rightarrow\Delta AMC=\Delta DMB\left(c.g.c\right)\\ \Rightarrow AC=BD;\widehat{CAM}=\widehat{MDB}\)
Mà \(\widehat{CAM}+\widehat{MAB}=\widehat{BAC}=90^0\Rightarrow\widehat{MDB}+\widehat{MAB}=90^0\)
Mà \(\widehat{MDB}+\widehat{MAB}+\widehat{DBA}=180^0\Rightarrow\widehat{DBA}=90^0\)
\(\left\{{}\begin{matrix}\widehat{DBA}=\widehat{BAC}\left(=90^0\right)\\AC=BD\\AB.chung\end{matrix}\right.\Rightarrow\Delta BAC=\Delta ABD\left(c.g.c\right)\\ \Rightarrow AD=BC\\ \Rightarrow AM=MB\left(\dfrac{1}{2}AD=\dfrac{1}{2}BC\right)\)
Do đó tam giác ABM cân tại M
Mà có \(\widehat{ABM}=60^0\) nên tam giác ABM đều
Vì tam giác ABM đều nên \(AB=BM=\dfrac{1}{2}BC\)
Đúng 2
Bình luận (0)
chứng tỏ AB//EF trong mỗi hình sauhình a A B C D E F 120 độ 60 độ 40 độ 140 độ hình b C D E F A B 30 độ 30 độ 40 độ 40 độ
Đọc tiếp
chứng tỏ AB//EF trong mỗi hình sau
hình a
hình b
hình a, ta thấy
\(\angle\left(A\right)+\angle\left(DCA\right)=120+60=180^0\)
mà 2 góc này ở vị trí trong cùng phía
\(=>AB//CD\left(1\right)\)
có \(\angle\left(DCE\right)+\angle\left(E\right)=40+140=180^O\)
mà 2 góc này ở vị trí trong cùng phía
\(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
hình b,
\(=\angle\left(BAD\right)=\angle\left(ADC\right)=30^0\)
mà 2 góc này ở vị trí so le trong \(=>AB//CD\left(1\right)\)
có \(\angle\left(CDE\right)=\angle\left(DEF\right)=40^o\)
mà 2 góc này ở vị trí so le trong \(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A (AB < AC) và ^B= 60° . gọi M là trung điểm của AC. trên tia BM lấy điểm D sao cho MB = MD a) tính số đo của ^C b) chứng minh ∆BMA=∆DMC c) chứng minh AB=CD d) chứng minh AB//CD
Xem chi tiết
a) Xét tam giác ABC có A+B+C=180o(tổng 3 góc của 1 tam giác )
mà A=90o,B=60o
=>C=180o-90o-60o=30o
vậy C=30o
Đúng 1
Bình luận (0)
Xét tam giác BMA và tam giác DMC có:
MB=MD(gt)
MA=MC(M là trung điểm của BC)
ABM=CMD(đối đỉnh)
=>tam giác BMA= tam giác DMC(c.g,c)
Đúng 0
Bình luận (0)
c) Vì tam giác BMA= tam giác DMC(câu b)
=> AB=CD(2 góc tương ứng)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang ABCD có AB//CD, AB>CD, góc C bằng 60 độ. Trên cạnh AB lấy M sao cho AM=AD
a) Chứng minh DM là tia phân giác của góc D
b) Tính góc MBC
a, Xét △ADM có: AM = AD (gt) => △ADM cân tại A
=> ADM = AMD
Mà AMD = MDC (AB // CD)
=> ADM = MDC
=> DM là phân giác ADC
b, Vì AB // CD => MBC + BCD = 180o (2 góc trong cùng phía)
=> MBC + 60o = 180o
=> MBC = 120o
(3.0 điểm). Cho tam giác ABC vuông tại A, có AB = 3cm, BC = 5cm. a) Tính độ dài AC ? b) Gọi M là trung điểm của AC, Trên tia đối của tia MB lấy điểm D sao cho MB = MD. Chứng minh rằng: ABM = CDM. Từ đó suy ra AB = CD. c) Chứng minh 2.BM < AB + BC.
a: AC=căn 5^2-3^2=4cm
b: Xét ΔMAB và ΔMCD có
MA=MC
góc AMB=góc CMD
MB=MD
=>ΔMAB=ΔMCD
=>AB=CD
c: AB+BC=CD+BC>DB=2BM(ĐPCM)
Đúng 0
Bình luận (0)
(3.0 điểm). Cho tam giác ABC vuông tại A, có AB = 3cm, BC = 5cm. a) Tính độ dài AC ? b) Gọi M là trung điểm của AC, Trên tia đối của tia MB lấy điểm D sao cho MB = MD. Chứng minh rằng: ABM = CDM. Từ đó suy ra AB = CD. c) Chứng minh 2.BM < AB + BC.
A) Vì tam giác ABC vuông tại A nên ta có :
AB2+AC2=BC2AB2+AC2=BC2
⇔AC2=BC2−AB2⇔AC2=BC2−AB2
⇔AC2=52−32⇔AC2=52−32
⇔AC2=25−9⇔AC2=25−9
⇔AC2=16⇔AC2=16
⇔AC=4
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB//CD), góc D 90 độ, góc C bằng 30 độa) Chứng minh rằng diện tích hình thanh ABCD 1/4*BC*(AB+CD)b) Gọi M là giao điểm của BC và AD. Kẻ DK vuông góc với CM (K thuộc CM), KL vuông góc với DM (L thuộc DM). Chứng minh rằng 4*DL*DMCD2 c) Biết BC 8cm, diện tích hình thang ABCD 48 cm2. Tính DM, MC (không làm tròn kết quả)Mng giúp mik với, mai mik ktra rồi
Đọc tiếp
Cho hình thang ABCD (AB//CD), góc D = 90 độ, góc C bằng 30 độ
a) Chứng minh rằng diện tích hình thanh ABCD = 1/4*BC*(AB+CD)
b) Gọi M là giao điểm của BC và AD. Kẻ DK vuông góc với CM (K thuộc CM), KL vuông góc với DM (L thuộc DM). Chứng minh rằng 4*DL*DM=CD2
c) Biết BC = 8cm, diện tích hình thang ABCD = 48 cm2. Tính DM, MC (không làm tròn kết quả)
Mng giúp mik với, mai mik ktra rồi
Cho xAy=40 độ, điểm B thuộc tia Ax. Trên nửa mặt phẳng bờ AB không chứa tia Ay, kẻ tia BM sao cho ABM=40 độ.
a) Chứng tỏ Bm//Ay
b) Vẽ tia Bt nằm trong góc xBm sao cho tBx=100 độ. Chứng tỏ rằng BM là tia phân giác của góc ABt.
c) Kéo dài tia đối Bt cắt tia Ay tại điểm C. Chứng tỏ rằng BAC=BCA
cho đoạn thẳng AB. Điểm C thuộc tia đối của tia BA. M là trung điểm của đoạn thẳng AB.
a) chứng tỏ rằng: CM=CA+CB / 2
b) gọi O là một điểm nằm ngoài đoạn thẳng AB. Biết góc aoc=120 độ, góc boc= 30 độ, góc aom=60 độ. Hỏi OB có phải là tia phân giác của góc moc không? vì sao?
giúp mik nhanh vs mik tick cho