/ X+2 / = 0

Những câu hỏi liên quan
cho hỏi làm thế này đúng k ạ :
x^2+2x-2=0
x.x+2.x-2=0
x(x+2)-2=0
+x=0
+(x+2)-2=0
x+2=0+2
x+2=2
x=2-2
x=0
Vậy :x=0
sai roi x(x+2)-2=0 thi x(x+2)=2 thi x thuoc uoc cua 2 con x-2=2/x con lai thi re roi
Đúng 0
Bình luận (0)
Bài 2: Tìm x
a) (x-2)2-(2x+3)20 d) x2.(x+1)-x.(x+1)+x.(x-1)0
b) 9.(2x+1)2-4.(x+1)20 e) (x-2)2-(x-2).(x+2)0
c) x3-6x2+9x0 g) x4-2x2+10
h) 4x2+y2-20x-2y+260 i) x2-2x+5+y2-4y0
Đọc tiếp
Bài 2: Tìm x
a) (x-2)2-(2x+3)2=0 d) x2.(x+1)-x.(x+1)+x.(x-1)=0
b) 9.(2x+1)2-4.(x+1)2=0 e) (x-2)2-(x-2).(x+2)=0
c) x3-6x2+9x=0 g) x4-2x2+1=0
h) 4x2+y2-20x-2y+26=0 i) x2-2x+5+y2-4y=0
a) Tính (theo mẫu).Mẫu: 0 x 2 ?0 x 2 0 + 0 00 x 2 00 x 3 0 x 4 0 x 5Nhận xét: Số 0 nhân với số nào cũng bằng 0.b) Tính nhẩm:0 x 6 0 x 7 0 x 8 0 x 90 : 6 0 : 7 0 : 8 0 : 9Nhận xét: Số 0 chia cho số nào khác 0 cũng bằng 0.
Đọc tiếp
a) Tính (theo mẫu).
Mẫu: 0 x 2 = ? 0 x 2 = 0 + 0 = 0 0 x 2 = 0 |
0 x 3 0 x 4 0 x 5
Nhận xét: Số 0 nhân với số nào cũng bằng 0.
b) Tính nhẩm:
0 x 6 0 x 7 0 x 8 0 x 9
0 : 6 0 : 7 0 : 8 0 : 9
Nhận xét: Số 0 chia cho số nào khác 0 cũng bằng 0.
a) \(0\times3=0\)
\(0\times4=0\)
\(0\times5=0\)
b) \(0\times6=0\)
\(0\times7=0\)
\(0\times9=0\)
\(0:6=0\)
\(0:7=0\)
\(0:8=0\)
\(0:9=0\)
Đúng 1
Bình luận (0)
tìm x: part 1 : a,(x^3)^2-(x+1)(x-1)=1 b,(x-2)^2-3(x-2)=0 c,(x+2)(x^2-2x+4)-x(x^2+2)=15 d,(x+1)^2-(x+1)(x-2)=0 e,4x(x-2017)-x+2017=0 f,(x+4)^2-16=0 part 2: a,x^3+27+(x+3)(x-9)=0 b,(2x-1)^2-4x^2+1=0 c,2(x-3)+x^2-3x=0 d,x^2-2x+1=6x-6 e,x^3-9x=0
Xem thêm câu trả lời
Giải phương trình
a) \(x^2-2x+1=0\)
b)\(1+3x+3x^2+x=0\)
c)\(x+x^4=0\)
d)\(x^3-3x^2+3x-1+x\left(x^2-x\right)=0\)
e)\(x^2+x-12=0\)
g)\(6x^2-11x-10=0\)
a) Ta có: \(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\)hay x=1
Vậy: S={1}
c) Ta có: \(x+x^4=0\)
\(\Leftrightarrow x\left(x^3+1\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(x^2-x+1\right)=0\)
mà \(x^2-x+1>0\forall x\)
nên x(x+1)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
Vậy: S={0;-1}
Đúng 2
Bình luận (1)
Tìm x
a.(x+4).(-3x+9)=0
b.(x^2 +1).(x-5)=0
c.(/x/ +2).(x^2-1)=0
d.(x^2 -3).(2 x^2 +10)=0
e.(x-2)^2 -25=0
(x-2).(x+2)<0
mình đang cần rất gấp mong các bạn giúp ,ngày mai mình phải nộp cho cô rồi .bạn nào làm nhanh mình k luôn nha
Đúng 0
Bình luận (0)
\(\left(x+4\right).\left(-3x+9\right)=\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=0\\-3x+9=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0-4\\-3x=0-9\end{cases}\Leftrightarrow}}\orbr{\begin{cases}x=-4\\-3x=-9\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-4\\x=\left(-9\right):\left(-3\right)\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-4\\x=3\end{cases}}}\)
Vậy .....................
~ Hok tốt ~
Đúng 0
Bình luận (0)
#)Giải ;
a)\(\left(x+4\right)\left(-3x+9\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+4=0\\-3x+9=0\end{cases}\Rightarrow\orbr{\begin{cases}x=-4\\-3x=-9\end{cases}\Rightarrow}\orbr{\begin{cases}x=-4\\x=3\end{cases}}}\)
Vậy \(x\in\left\{-4;3\right\}\)
b)\(\left(x^2+1\right)\left(x-5\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x^2+1=0\\x-5=0\end{cases}\Rightarrow\orbr{\begin{cases}x^2=-1\\x=5\end{cases}\Rightarrow}\orbr{\begin{cases}x=-1\\x=5\end{cases}}}\)
Vậy \(x\in\left\{-1;5\right\}\)
c)\(\left(\left|x\right|+2\right)\left(x^2-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}\left|x\right|+2=0\\x^2-1=0\end{cases}\Rightarrow\orbr{\begin{cases}\left|x\right|=-2\\x^2=1\end{cases}\Rightarrow}\orbr{\begin{cases}x=2;x=-2\\x=1\end{cases}}}\)
Vậy \(x\in\left\{2;-2;1\right\}\)
d)\(\left(x^2-3\right)\left(2x^2+10\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x^2-3=0\\2x^2+10=0\end{cases}\Rightarrow\orbr{\begin{cases}x^2=3\\2x^2=-10\end{cases}\Rightarrow}\orbr{\begin{cases}x=\sqrt{3}\\x^2=-5\end{cases}\Rightarrow}\orbr{\begin{cases}x=\sqrt{3}\\x=\sqrt{-5}\end{cases}}}\)
Vậy \(x\in\left\{\sqrt{3};\sqrt{-5}\right\}\)
Đúng 0
Bình luận (0)
Tìm x nguyên biết :
a) (x^2 -5)×(x^2 +1)=0
b)(x+3)×(x^2+1)=0
c)(x+5)×(x^2+1)<0
d)(x+5)×(x^2-4)=0
e)(x-2)×(-x^2-4)>0
g)(x^2+2)×(x+3)>0
h)(x+4)×|x+5|>0
i)(x+3)×(x-5)>0
\(\left(x^2-5\right)\left(x^2+1\right)=0\)
<=> \(\hept{\begin{cases}x^2-5=0\\x^2+1=0\end{cases}}\)
<=> \(\hept{\begin{cases}x^2=5\\x^2=-1\end{cases}}\)
<=> \(\hept{\begin{cases}x=\sqrt{5};x=-\sqrt{5}\\x\in\varnothing\end{cases}}\)
câu còn lại tương tự nha
Đúng 0
Bình luận (0)
Giải các bất phương trình sau:
a) \(2{x^2} + 3x + 1 \ge 0\)
b) \( - 3{x^2} + x + 1 > 0\)
c) \(4{x^2} + 4x + 1 \ge 0\)
d) \( - 16{x^2} + 8x - 1 < 0\)
e) \(2{x^2} + x + 3 < 0\)
g) \( - 3{x^2} + 4x - 5 < 0\)
a) \(2{x^2} + 3x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x = - 1,x = \frac{{ - 1}}{2}\)
hệ số \(a = 2 > 0\)
Ta có bảng xét dấu f(x) như sau:
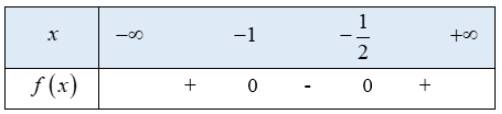
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 1\\x \ge - \frac{1}{2}\end{array} \right.\)
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)
b) \( - 3{x^2} + x + 1 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)
Hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)
Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)
c) \(4{x^2} + 4x + 1 \ge 0\)
Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)
hệ số \(a = 4 > 0\)
Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)
d) \( - 16{x^2} + 8x - 1 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)
hệ số \(a = - 16 < 0\)
Ta có bảng xét dấu f(x) như sau:
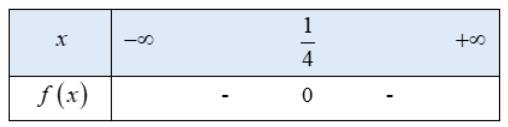
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)
e) \(2{x^2} + x + 3 < 0\)
Ta có \(\Delta = {1^2} - 4.2.3 = - 23 < 0\) và có \(a = 2 > 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)
Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)
g) \( - 3{x^2} + 4x - 5 < 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) = - 11 < 0\) và có \(a = - 3 < 0\)
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)
Đúng 0
Bình luận (0)
2/3(x22-4)=0
(x+5)2-(x+2)(x-3)=-1
x22-4+(xx-2)2=0.
2x2-6x=0
2x(x+2)-3(x+2)=0
(x+3)(x-3)+x(5-x)=-14
x(x-3)-x22+5=0
2x33+5x2-12x=0
x2-5x-24=0
x2-x-6=0
x22-6x+8=0
x3-16x=0
\(2x^2-6x=0\)
\(\Rightarrow2x.\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0:2\\x=0+3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy \(x\in\left\{0;3\right\}.\)
\(2x.\left(x+2\right)-3.\left(x+2\right)=0\)
\(\Rightarrow\left(x+2\right).\left(2x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\2x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0-2\\2x=3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=3:2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=\frac{3}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{-2;\frac{3}{2}\right\}.\)
\(x^3-16x=0\)
\(\Rightarrow x.\left(x^2-16\right)=0\)
\(\Rightarrow x.\left(x^2-4^2\right)=0\)
\(\Rightarrow x.\left(x-4\right).\left(x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x-4=0\\x+4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=0+4\\x=0-4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
Vậy \(x\in\left\{0;4;-4\right\}.\)
Chúc bạn học tốt!
Tìm x biết:
a) x^2-3.x=0
b) 2.x^2+5.x=0
c) x^2+1=0
d) x^2-1=0
e) x.(x-3)-x+3=0
g) x^2.(x+2)-9.x-18=0
a)x^2-3.x=0
x^3.(1-3)=0
x^3.(-2)=0
x^3=0:(-2)
x^3=0
x=0
b)2.x^2+5.x=0
x^3.(2+5)=0
x^3.7=0
x^3=0:7
x^3=0
x=0
c)x^2+1=0
x^2=0-1
x^2=(-1)
x ko thỏa mãn
d)x^2-1=0
x^2=0+1
x^2=1
x=1 hoặc x=(-1)
e)x.(x-3)-x+3=0
Mình ko bt xin lỗi
g)x^2.(x+2)-9.x-18=0
x^2.(x+2)-9.x=0+18
x^2.(x+2)-9.x=18
x^2.x+x^2.2-9.x=18
Mk chỉ giải đc đến đây thôi. Xin lỗi!
Đúng 0
Bình luận (1)
























