Cho ΔABC, BD ⊥ AC tại D và CE ⊥ AB tại E. BD ⋂ CE tại H. BD = CE.
a) CM: ΔABC cân
b) CM: ΔHBC cân

Những câu hỏi liên quan
cho ΔABC cân tại A (A<90\(^o\)). Kẻ BD⊥AC(D∈AC), CE⊥AB(E∈AB). BD và CE cắt nhau tại H.
a, ΔABD = ΔACE
b, so sánh góc ABD và góc ACE
c, Kéo dài AH cắt BC tại K. C/M AK⊥BC
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
b: ΔABD=ΔACE
=>góc ABD=góc ACE
c: Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
=>AH vuông góc BC tại K
Đúng 0
Bình luận (0)
Bài 5: Cho ΔABC cân tại A có AB AC 6cm; BC 4cm. Các đường phân giác BD và CE cắt nhau tại I (E trên AB và D trên AC)a. Tính độ dài AD, ED.b. Cm ΔADB đồng dạng với ΔAECc. Cm IE.CD ID.BEd. Cho SABC 60 cm². Tính SAED.
Đọc tiếp
Bài 5: Cho ΔABC cân tại A có AB = AC = 6cm; BC = 4cm. Các đường phân giác BD và CE cắt nhau tại I (E trên AB và D trên AC)
a. Tính độ dài AD, ED.
b. Cm ΔADB đồng dạng với ΔAEC
c. Cm IE.CD = ID.BE
d. Cho SABC = 60 cm². Tính SAED.
a: Xét ΔBAC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/2=6/5=1,2
=>AD=3,6cm; CD=2,4cm
Xét ΔABCcó ED//BC
nên ED/BC=AD/AC
=>ED/4=3,6/6=3/5
=>ED=2,4cm
b: Xét ΔADB và ΔAEC có
góc A chung
góc ABD=góc ACE
=>ΔABD đồng dạng với ΔACE
c: Xét ΔIEB và ΔIDC có
góc IEB=góc IDC
góc EIB=góc DIC
=>ΔIEB đồng dạng với ΔIDC
=>EB/DC=IE/ID
=>IE*DC=EB*ID
Đúng 0
Bình luận (0)
cho tam giác nhọn ABC có AB=AC . Kẻ BD ⊥ với AC tại D , kẻ CE⊥AB tại E . Gọi I là giao điểm của BD và CE.
a) CM △ ABD =△ACE
b) CM EI=DI
c) CM AI⊥BC
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: ΔABD=ΔACE
=>AD=AE
Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
Do đó: ΔAEI=ΔADI
=>EI=DI
c: ΔABD=ΔACE
=>BD=CE
BI+DI=BD
CI+EI=CE
mà EI=DI và BD=CE
nên BI=CI
IB=IC
AB=AC
Do đó: AI là đường trung trực của BC
=>AI\(\perp\)BC
Đúng 0
Bình luận (0)
Cho ΔABC cân tại A ( góc A < 90 độ ) . Kẻ BD ⊥ AC tại D , kẻ CE ⊥ AB tại E
a, Chứng minh ΔADE CÂN
b, DE // BC
c, Gọi I là giao diểm của BD và CE . Chứng minh IB = IC
d, AI ⊥ BC
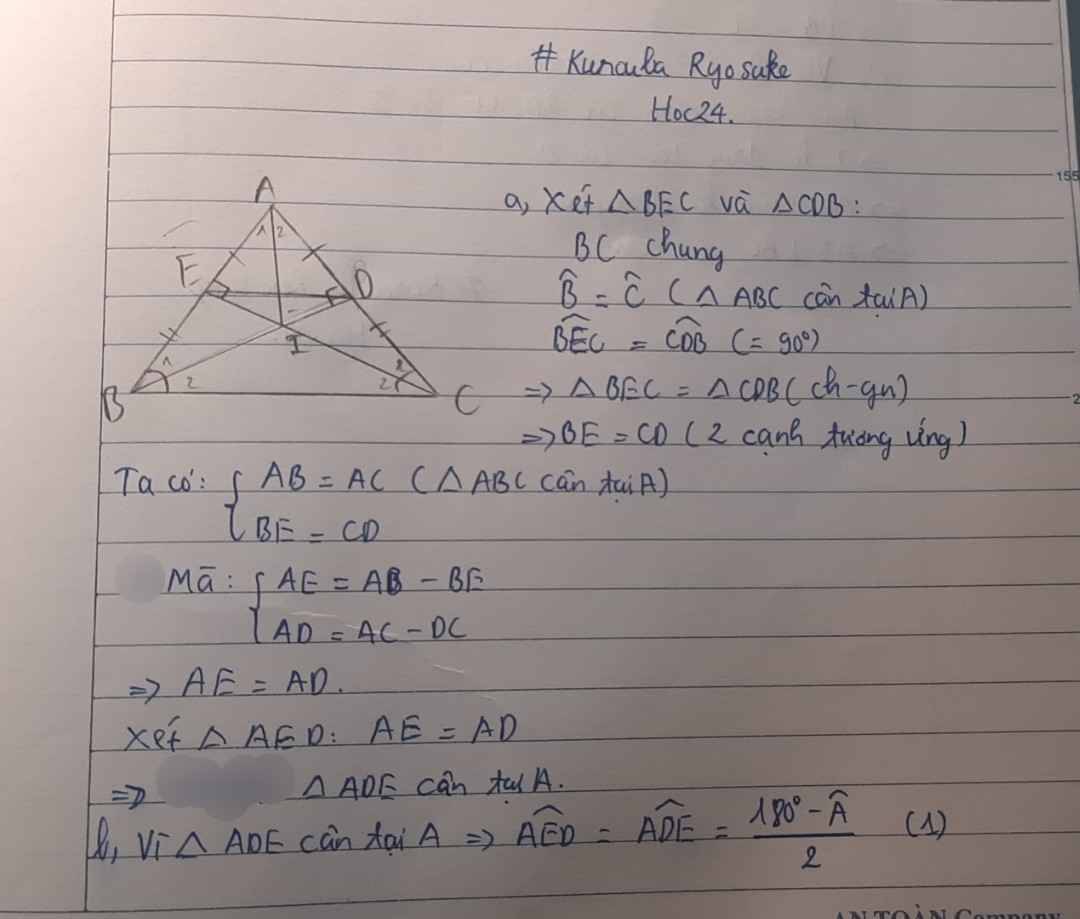

* câu d, í cậu, nếu cậu chưa học về các đường và t/c của tam giác cân với các đường đó thì bảo mk để mk làm lại cách khác cho nha :vv.
Đúng 3
Bình luận (2)
cho tam giác ABC cân tại A ( A < 90 độ ) . Kẻ BD vuông góc Ac ( D thuộc AC ) , CE vuông góc AB ( E thuộc AB ) , BD và CE cắt nhau tại H . a, CM : BD = CE . b, CM : tam giác BHC cân . c, CM : AH là đường trung trực của BC . d, TRên tia BD lấy điểm K sao cho D là trung điểm của BK . So sánh ECB và DKC
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔAEC
=>BD=CE
b: góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC
Đúng 0
Bình luận (0)
Cho ΔABC cân tại A. Vẽ AH⊥BC tại H.
a) CM: ΔABH=ΔACH.
b) Trên tia đối tia CB lấy điểm NN, trên tia đối của tia BC lấy điểm M sao cho BM=CN. CM:ΔAMN cân
c)Kẻ BD⊥AM tại điểm D, CE⊥ AN tại E, CE cắt BD tạu K. CM: 3điểm A, H, K thẳng hàng
a, Do tam giác ABC cân tại A(gt) => AB=AC
Do AH\(\perp\)BC(gt)=> \(\widehat{AHB}=\widehat{AHC}=90^o\)
Xét tam giác ABH và tam giác ACH có:
\(\widehat{AHB}=\widehat{AHC}=90^o\left(cmt\right)\)
AB=AC(cmt)
AH chung
=> tam giác ABH=tam giác ACH(ch-cgv)
b, Do tam giác ABH=tam giác ACH(câu a)
\(\)=> HB=HC (2 cạnh tương ứng)
Do tam giác ABC cân tại A(gt)=> \(\widehat{ABC}=\widehat{ABC}\)
Ta có: \(\widehat{ABC}+\widehat{ABM}=180^o\)(kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^o\)(kề bù)
\(\Rightarrow\widehat{ABM}=\widehat{ACN}\)
Xét tam giác ABM và tam giác ACN có:
AB=AC(câu a)
\(\widehat{ABM}=\widehat{ACN}\left(cmt\right)\)
BM=CN(gt)
=>tam giác ABM và tam giác ACN(c.g.c)
\(\Rightarrow AM=AN\) (2 cạnh tương ứng)
\(\Rightarrow\Delta AMN\) cân tại A
Đúng 0
Bình luận (0)
Cho ΔABC cân tại (Â < 90 độ). Kẻ BD ⊥ AC (D ∈ AC), CE ⊥ AB (E ∈ AB), BD và CE cắt nhau tại H.
a. Chứng minh: BD = CE.
b. Chứng minh: ΔBHC cân.
c. Chứng minh: AH là đường trung trực của BC.
d. Trên tia BD lấy điểm K sao cho D là trung điểm của BK. So sánh: góc ECB và góc DKC.
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔBHC có \(\widehat{HBC}=\widehat{HCB}\)
nên ΔBHC cân tại H
c: Ta có: AB=AC
HB=HC
Do đó: AH là đường trung trựuc của BC
Đúng 1
Bình luận (1)
ΔABC cân tại A (góc A <90 độ) BD vuông góc AC và CE vuông góc AB (D,EϵAC, AB). BD cắt CE = {H}
a) ΔABD=ΔACE
b) ΔBHC cân
c) ED // BC
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc A chung
=>ΔADB=ΔAEC
b: góc ABD+góc HBC=góc ABC
góc ACE+gócHCB=góc ACB
mà góc ABD=góc ACE; góc ABC=góc ACB
nên góc HBC=góc HCB
=>ΔHBC cân tạiH
c: Xet ΔBAC có AE/AB=AD/AC
nên ED//BC
Đúng 1
Bình luận (0)
`a,`
Xét Tam giác `ABD` và Tam giác `ACE` có:
`AB = AC (\text {Tam giác ABC cân tại A})`
\(\widehat{A} \) \(\text {chung}\)
`=> \text {Tam giác ABD = Tam giác ACE (ch-gn)}`
`b,`
Vì Tam giác `ABD =` Tam giác `ACE (a)`
`-> AD = AE (\text {2 cạnh tương ứng})`
`->`\(\widehat{ABD}=\widehat{ACE} (\text {2 góc tương ứng})\)
Ta có: \(\left\{{}\begin{matrix}AB=AE+BE\\AC=AD+DC\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}AB=AC\left(gt\right)\\AD=AE\left(CMT\right)\end{matrix}\right.\)
`-> BE = DC`
Xét Tam giác `HEB` và Tam giác `HDC` có:
\(\widehat{HBE}=\widehat{HCD} (CMT)\)
`BE = DC (CMT)`
\(\widehat{HEB}=\widehat{CDH}=90^0\)
`=> \text {Tam giác HEB = Tam giác HDC}`
`-> HB = HC (\text {2 cạnh tương ứng})`
Xét Tam giác `BHC: HB = HC`
`->` Tam giác `BHC` cân tại `H`
`c,`
Xét Tam giác `AED: AE = AD (CMT)`
`-> \text {Tam giác AED cân tại A}`
`->`\(\widehat{AED}=\widehat{ADE} =\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `ABC` cân tại `A:`
`->`\(\widehat{ACB}=\widehat{ACB}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{AED}=\widehat{ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {ED = BC (đpcm)}.`

Đúng 2
Bình luận (0)
Bài 1:Cho ΔABE vuông cân tại A. Qua A vẽ D sao cho B và C cùng nửa mặt phẳng bờ d. Vẽ BD và CE ⊥ với d.
a,CMR ΔDBA=ΔEAC
b,CMR BD+CE=DE
bài 2:cho ΔABC vuông góc tại A có AB<AC, vẽ AH ⊥ BC. D là điểm nằm trên AC sao cho AD=AB, vẽ DE ⊥ BC. CM HA=HE
1:
a:
góc DAB+góc CAE=180 độ-góc BAE=90 độ
góc DAB+góc DBA=90 độ
=>góc DBA=góc CAE
Xét ΔDBA vuông tại D và ΔEAC vuông tại E có
BA=AC
góc DBA=góc EAC
=>ΔDBA=ΔEAC
b: ΔDBA=ΔEAC
=>DB=EA và DA=EC
BD+CE
=CA+AD
=CD
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ BD vuông góc AB (EϵAB).BD và CE cắt nhau tại I:
a)CIm rằng ΔABC =ΔCEB
b)C/M Góc IBE= Góc ICD
c)Đường thẳng AI cắt BC tại H .CM rằng AI vuông góc với BC tại H
Sửa đề: BD vuông góc với AC, CE vuông góc với AB
a) Sửa đề: Chứng minh ΔBDC=ΔCEB
Xét ΔBDC vuông tại D và ΔCEB vuông tại E có
BC chung
\(\widehat{DCB}=\widehat{ECB}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBDC=ΔCEB(cạnh huyền-góc nhọn)
Đúng 3
Bình luận (0)



















