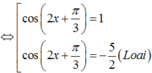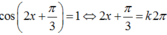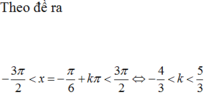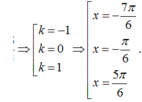2cos2 x - có x -1=0

Những câu hỏi liên quan
Phương trình 2cos2 x + 3cosx - 2 0 có nghiệm là
Đọc tiếp
Phương trình 2cos2 x + 3cosx - 2 = 0 có nghiệm là
![]()
![]()
![]()
![]()
Giải phương trình : cos2x + cosx = 2cos2\(\dfrac{x}{2}\)
\(\Leftrightarrow2cos^2x-1+cosx=cosx+1\)
\(\Leftrightarrow2cos^2x=2\)
\(\Leftrightarrow sin^2x=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)
Đúng 0
Bình luận (0)
Hàm số y = 2cos2 x + 3cos3x + 8cos4x tuần hoàn với chu kì
A. π
B. 2π
C. 3π
D. 4π
Đáp án B
+ y = 2 cos2 x + 3cos3x + 8cos4x = 4 + 9/4 cos x + 5cos 2x + 3/4 cos 3x + cos 4x
+ Hàm số y = 9/4cos x tuần hoàn với chu kì 2π.
+ Hàm số y = 5cos 2x tuần hoàn với chu kì 2π/2 = π .
+ Hàm số y = 3/4 cos 3x tuần hoàn với chu kì 2π/3.
+ Hàm số y = cos 4x tuần hoàn với chu kì 2π/4 = π/2.
+ Do đó hàm số y = 2 cos2 x + 3cos3x + 8cos4x là hàm tuần hoàn với chu kì 2π.
Chú ý:

Đúng 0
Bình luận (0)
cos(4x) + cos(2x) +sin(2x) +2 = 2\(\sqrt{2}\) sin(x+π/4)+2cos2(2x)
Nghiệm của phương trình
2
cos
2
(
2
x
+
π
3
)
+
3
cos
(
2
x
+
π
3
)
-
5
0
trong khoảng
-
3
π
2...
Đọc tiếp
Nghiệm của phương trình 2 cos 2 ( 2 x + π 3 ) + 3 cos ( 2 x + π 3 ) - 5 = 0 trong khoảng - 3 π 2 ; 3 π 2 là:
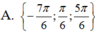
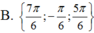
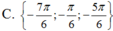
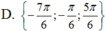
sin5x+sin3x+2cos2=1+sin4x
\(\sin\left(5x\right)+\sin\left(3x\right)+2\cos\left(x\right)=1+\sin\left(4x\right)\)
\(\Leftrightarrow2\sin\left(4x\right)\cos\left(x\right)-\sin\left(4x\right)+2\cos\left(x\right)-1=0\)
\(\Leftrightarrow\sin\left(4x\right)(2\cos\left(x\right)-1)+(2\cos\left(x\right)-1)=0\)
\(\Leftrightarrow(2\cos\left(x\right)-1)(\sin\left(4x\right)+1)=0\)
\(\Rightarrow\left[{}\begin{matrix}\cos\left(x\right)=\dfrac{1}{2}\\\sin\left(4x\right)=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k2\pi\\4x=\dfrac{-\pi}{2}+k2\pi\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k2\pi\\x=\dfrac{-\pi}{8}+k\dfrac{\pi}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
chứng minh:
\(\dfrac{2cos2\alpha-sin4\alpha}{2cos2\alpha+sin4\alpha}=tan^2\left(\dfrac{\pi}{4}-\alpha\right)\)
chứng minh:
\(\dfrac{1}{sin\alpha}+\dfrac{1}{sin2\alpha}+\dfrac{1}{sin4\alpha}+....+\dfrac{1}{sin2^n.\alpha}=\dfrac{cot\alpha}{2}-2cos2^n\alpha\)
Cường độ của một dòng điện xoay chiều qua điện trở R 10
Ω
có biểu thức
i
2
cos
2
(
100
πt
)
+
4
cos
3
(
100
πt
)
(
A
)
. Cường độ này có giá trị trung bình trong một chu kì bằng bao nhiêu? Tính cường độ hiệu dụng, công suất tỏa nhiệt và nhiệt lượng tỏa ra trên R...
Đọc tiếp
Cường độ của một dòng điện xoay chiều qua điện trở R = 10 Ω có biểu thức i = 2 cos 2 ( 100 πt ) + 4 cos 3 ( 100 πt ) ( A ) . Cường độ này có giá trị trung bình trong một chu kì bằng bao nhiêu? Tính cường độ hiệu dụng, công suất tỏa nhiệt và nhiệt lượng tỏa ra trên R trong thời gian 1 phút.
A. 3900J
B. 4000J
C. 2000J
D. Không đáp án nào đúng
Tìm m để :
1) (m + 1)\(x^2\) - 2(m + 1)x + 3m - 3 < 0 có nghiệm
2) \(x^2\) + 2(m + 2)x - 2m - 1 > 0 có nghiệm
3) (m-1)\(x^2\) - 2(m + 1)x + 3m - 6 ≤ 0 có nghiệm
a.
- Với \(m=-1\) BPT có nghiệm (đúng với mọi x)
- Với \(m\ne-1\) BPT có nghiệm khi:
\(\left[{}\begin{matrix}m+1< 0\\\left\{{}\begin{matrix}m+1>0\\\Delta'=\left(m+1\right)^2-\left(m+1\right)\left(3m-3\right)>0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\\left\{{}\begin{matrix}m>-1\\\left(m+1\right)\left(4-2m\right)>0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\\left\{{}\begin{matrix}m>-1\\-1< m< 2\end{matrix}\right.\end{matrix}\right.\)
Kết hợp lại ta được: \(m< 2\)
b.
Do \(a=1>0\) nên BPT có nghiệm với mọi m
c.
- Với \(m=1\) BPT có nghiệm
- Với \(m\ne1\) BPT có nghiệm khi:
\(\left[{}\begin{matrix}m-1< 0\\\left\{{}\begin{matrix}m-1>0\\\Delta'=\left(m+1\right)^2-\left(m-1\right)\left(3m-6\right)\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< 1\\\left\{{}\begin{matrix}m>1\\-2m^2+11m-5\ge0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< 1\\\left\{{}\begin{matrix}m>1\\\dfrac{1}{2}\le m\le5\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m< 1\\1< m\le5\end{matrix}\right.\)
Kết hợp lại ta được: \(m\le5\)
Đúng 2
Bình luận (0)