\(\Leftrightarrow2cos^2x-1+cosx=cosx+1\)
\(\Leftrightarrow2cos^2x=2\)
\(\Leftrightarrow sin^2x=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)
Giải phương trình:
\(\dfrac{1+cos2x\times cosx}{cos^2x}+2\left(sin^4x+cos^4x\right)=3\)
Tìm số điểm biểu diễn nghiệm của phương trình \(\dfrac{cos2x-cosx}{\sqrt{cosx}}=0\) trên vòng tròn lượng giác
Giải phương trình : sinx + sin2x = cosx + cos2x
Giải phương trình cos3x + cos2x - cosx - 1 = 0
Giải phương trình
cos2x + cosx + 1= sin2x+sinx
Giải phương trình sinx + sin2x + sin3x= cosx + cos2x+ cos3x
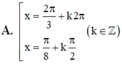
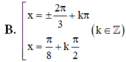
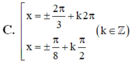
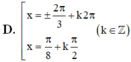
Giải phương trình: √3.cos2x-sin2x = √3.sinx + cosx
Giải phương trình: sinx + cosx + 1 + sin2x + cos2x = 0
giải phương trình
a) \(sinx=sin\dfrac{\pi}{4}\)
b) \(cos2x=cosx\)
c) \(tan\left(x-\dfrac{\pi}{3}\right)=\sqrt{3}\)
d) \(cot\left(2x+\dfrac{\pi}{6}\right)=cot\dfrac{\pi}{4}\)
