Tính giá trị của các biểu thức 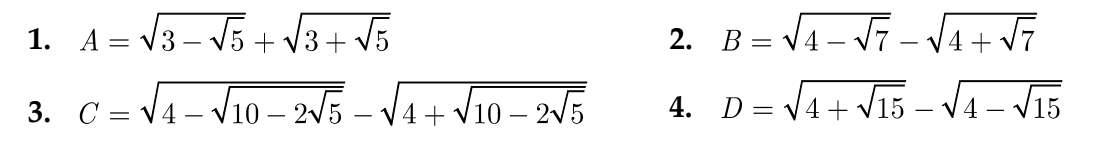

Những câu hỏi liên quan
Cho biểu thức với . a) Rút gọn biểu thức ; b) Tìm điều kiện của để ; c) Tìm các giá trị nguyên của để có giá trị nguyên; d)* Với , hãy tìm giá trị lớn nhất của . Bài 8: Cho biểu thức ; với . a) Tính giá trị biểu thức khi . b) Rút gọn biểu thức . c) So sánh với 1. d) Tìm để có giá trị nguyên.
a) Viết tiếp vào chỗ chấm cho thích hợp :Khi tính giá trị của biểu thức có chứa dấu ( ) thì ta thực hiện các phép tính ....... trước.b) Tính :3 x (17 + 22) ...... ......Giá trị của biểu thức 3 x (17 + 22) là ......(58 – 23) : 5 ........ ......Giá trị của biểu thức (58 – 23) : 5 là ........
Đọc tiếp
a) Viết tiếp vào chỗ chấm cho thích hợp :
Khi tính giá trị của biểu thức có chứa dấu ( ) thì ta thực hiện các phép tính ....... trước.
b) Tính :
3 x (17 + 22) = ...... = ......
Giá trị của biểu thức 3 x (17 + 22) là ......
(58 – 23) : 5 = ........ = ......
Giá trị của biểu thức (58 – 23) : 5 là ........
a) Khi tính giá trị của biểu thức có chứa dấu ( ) thì ta thực hiện các phép tính trong ngoặc trước.
b) Tính :
3 x (17 + 22) = 3 x 39 = 117
Giá trị của biểu thức 3 x (17 + 22) là 117.
(58 – 23) : 5 = 35 : 5 = 7.
Giá trị của biểu thức (58 – 23) : 5 = 7.
Đúng 0
Bình luận (0)
Với a = 8 thì giá trị của biểu thức 127 + 8 x 6 = 127 + 48 = 175
Đúng 0
Bình luận (0)
a) Khi tính giá trị của biểu thức có chứa dấu ( ) thì ta thực hiện các phép tính trong ngoặc trước.
b) Tính :
3 x (17 + 22) = 3 x 39
= 117
Giá trị của biểu thức 3 x (17 + 22) là : 117
(58 – 23) : 5 = 35 : 5
= 7
Giá trị của biểu thức (58 – 23) : 5 là 7
Chúc lm bài tốt
Cho biểu thức: P và Q (ĐKXĐ: )1. Tính giá trị của biểu thức P khi 2. Rút gọn biểu thức Q.Tìm các số hữu tỉ a để biểu thức M P.Q có giá trị nguyên
Đọc tiếp
Cho biểu thức: P =  và Q =
và Q =  (ĐKXĐ:
(ĐKXĐ: ![]() )
)
1. Tính giá trị của biểu thức P khi ![]()
2. Rút gọn biểu thức Q.
Tìm các số hữu tỉ a để biểu thức M = P.Q có giá trị nguyên
1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: 1.1. Tính giá trị biểu thức: vdn1.1. Tính giá trị biểu thức:
Đọc tiếp
1.1. Tính giá trị biểu thức:
1.1. Tính giá trị biểu thức: ![]() 1.1. Tính giá trị biểu thức:
1.1. Tính giá trị biểu thức: ![]()
1.1. Tính giá trị biểu thức:
1.1. Tính giá trị biểu thức: ![]()
1.1. Tính giá trị biểu thức: ![]()
vdn1.1. Tính giá trị biểu thức: ![]()
Ảnh hiển thị bị lỗi hết rồi bạn. Bạn coi lại.
Đúng 0
Bình luận (0)
Cho biểu thức
1 3 1
. 1 1 2
x x x A
x x
1) Tìm điều kiện của x để biểu thức A được xác định. 2) Rút gọn biểu thức A. 3) Tính giá trị của biểu thức A tại x 5. 4) Tìm các giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
1. ĐKXĐ: \(x\ne\pm1\)
2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x-3}{x-1}\)
3. Tại x = 5, A có giá trị là:
\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)
4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)
Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)
Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)
Đúng 1
Bình luận (0)
a) Tính giá trị của các biểu thức sau:
(300 + 70) + 500
300 + (70 + 500)
(178 + 214) + 86
178 + (214 + 86)
b) Nhận xét về giá trị của các biểu thức trong từng cột ở câu a.
c) Lấy ví dụ tương tự như các biểu thức ở câu a.
`(300+70)+500 = 370+500=870`
`300+(70+500)=300+570=870`
`(178+214)+86=392+86=478`
` 178+(214+86)=178+300 = 478`
`b,` Giá trị của biểu thức `(300 + 70) + 500, 300 + (70 + 500)` bằng nhau `(=870)`
`-` Giá trị của biểu thức `(178 + 214) + 86, 178 + (214 + 86)` bằng nhau `(=478)`
`c,` `25+(30+45) = 25+75 = 100`
` (25+30)+45 = 55+45=100`
Đúng 2
Bình luận (0)
Cho \(A = - ( - 4x + 3y),B = 4x + 3y,C = 4x - 3y\). Khi tính giá trị của biểu thức tại \(x = - 1\) và \(y = - 2\), bạn An cho rằng giá trị của các biểu thức A và B bằng nhau, bạn Bình cho rằng giá trị của các biểu thức A và C bằng nhau. Theo em, bạn nào đúng? Vì sao?
Thay giá trị \(x = - 1\) và \(y = - 2\) vào các biểu thức đã cho, ta có:
\(A = - ( - 4x + 3y) = - ( - 4. - 1 + 3. - 2) = - (4 + - 6) = - ( - 2) = 2\).
\(B = 4x + 3y = 4. - 1 + 3. - 2 = - 4 + - 6 = - 10\).
\(C = 4x - 3y = 4.( - 1) - 3.( - 2) = - 4 - - 6 = - 4 + 6 = 2\).
Ta thấy 2 ≠ -2 = 2. Do vậy, khi thay giá trị \(x = - 1\) và \(y = - 2\) vào các biểu thức đã cho ta thấy giá trị của các biểu thức A và C bằng nhau.
Vậy bạn Bình nói đúng.
Đúng 0
Bình luận (0)
Bài 4: Cho biểu thức M (với x) a) Rút gọn M b) Tính giá trị của biểu thức M với x - 3Bài 5. Cho hai biểu thức: A và B a) Tính giá trị của biểu thức A khi x 5b) Rút gọn biểu thức Bc) Biết P A.B, tìm các số tự nhiên x để P ∈ Z
Đọc tiếp
Bài 4: Cho biểu thức M = ![]() (với x
(với x![]() )
)
a) Rút gọn M
b) Tính giá trị của biểu thức M với x = - 3
Bài 5. Cho hai biểu thức: A = ![]() và B =
và B = ![]()
a) Tính giá trị của biểu thức A khi x = 5
b) Rút gọn biểu thức B
c) Biết P = A.B, tìm các số tự nhiên x để P ∈ Z
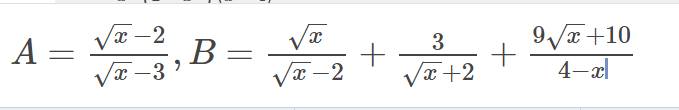
a,tính giá trị biểu thức A khi x=16/9
b,rút gọn biểu thức B
c,cho P=B/A,Tìm các giá trị của x là số thực đẻ P nhận giá trị nguyên
a: Khi x=16/9 thì \(A=\left(\dfrac{4}{3}-2\right):\left(\dfrac{4}{3}-3\right)=\dfrac{-2}{3}:\dfrac{-5}{3}=\dfrac{2}{5}\)
b: \(=\dfrac{x+2\sqrt{x}+3\sqrt{x}-6-9\sqrt{x}-10}{x-4}\)
\(=\dfrac{x-4\sqrt{x}-16}{x-4}\)
Đúng 1
Bình luận (0)
Tính giá trị của các biểu thức.

a) $\frac{9}{{14}} - \frac{2}{7} + \frac{1}{7} = \frac{9}{{14}} - \frac{4}{{14}} + \frac{2}{{14}} = \frac{{9 - 4 + 2}}{{14}} = \frac{7}{{14}} = \frac{1}{2}$
b) $\frac{7}{{10}} + \frac{{12}}{{25}}:\frac{4}{5} = \frac{7}{{10}} + \frac{{12}}{{25}} \times \frac{5}{4} = \frac{7}{{10}} + \frac{3}{5} = \frac{7}{{10}} + \frac{6}{{10}} = \frac{{13}}{{10}}$
c) $1:\frac{3}{5} \times \frac{9}{{10}} = 1 \times \frac{5}{3} \times \frac{9}{{10}} = \frac{5}{3} \times \frac{9}{{10}} = \frac{{5 \times 3 \times 3}}{{3 \times 5 \times 2}} = \frac{3}{2}$
d) $\left( {\frac{{15}}{{10}} - \frac{1}{2}} \right) \times \frac{{32}}{{35}} = \left( {\frac{3}{2} - \frac{1}{2}} \right) \times \frac{{32}}{{35}} = 1 \times \frac{{32}}{{35}} = \frac{{32}}{{35}}$
Đúng 0
Bình luận (0)
























