Mong làm chi tiết vs dịch nghĩa cho e vs ạ

Những câu hỏi liên quan
làm chi tiết vs e ạ
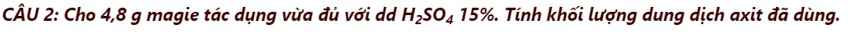
Câu 2 :
\(n_{Mg}=\dfrac{4,8}{24}=0,2\left(mol\right)\)
Pt : \(Mg+H_2SO_4\rightarrow MgSO_4+H_2|\)
1 1 1 1
0,2 0,2
\(n_{H2SO4}=\dfrac{0,2.1}{1}=0,2\left(mol\right)\)
\(m_{H2SO4}=0,2.98=19,6\left(g\right)\)
\(m_{ddH2SO4}=\dfrac{19,6.100}{15}\simeq130,67\left(g\right)\)
Chúc bạn học tốt
Đúng 1
Bình luận (0)
\(n_{Mg}=\dfrac{4,8}{24}=0,2\left(mol\right)\\ Mg+H_2SO_4->MgSO_4+H_2\\ m_{H_2SO_4=0,2\cdot98=19,6\left(g\right)}\)
\(m_{dd}=\dfrac{m_{ct}\cdot100}{C\%}=\dfrac{19,6\cdot100}{15}=130,6\left(g\right)\)
Đúng 0
Bình luận (0)
Giúp e chi tiết vs ạ
a: AO=a*căn 3/3
=>SO=a*căn 6/3
b: (SA,(ABC))=(AS;AO)=góc SAO
tan SAO=SO/OA=căn 2
=>góc SAO=55 độ
Đúng 0
Bình luận (0)
MN giúp e gấp vs ạ chi tiết ra giúp e ạ tks 
Bài 2
a, bạn tự vẽ
b, Hoành độ giao điểm tm pt
\(2x^2-2x+3=0\)
\(\Delta'=1-3.2=-5< 0\)
Vậy pt vô nghiệm hay (d) ko cắt (P)
Đúng 0
Bình luận (0)
Mn giúp mới giải vs ạ, mik cảm ơn nhiều, mai mik nộp cô rôi, mong mn giả chi tiết ạ
Mn giúp mới giải vs ạ, mik cảm ơn nhiều, mai mik nộp cô rôi, mong mn giả chi tiết ạ
Mn giúp mới giải vs ạ, mik cảm ơn nhiều, mai mik nộp cô rôi, mong mn giả chi tiết ạ
Mn giúp mới giải vs ạ, mik cảm ơn nhiều, mai mik nộp cô rôi, mong mn giả chi tiết ạ
Gấp vs ạ mn giải chi tiết giúp e ạ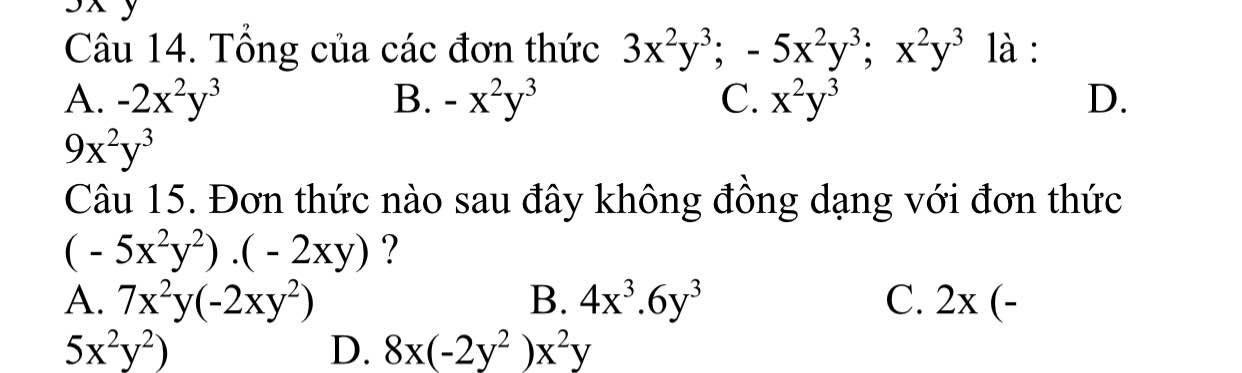
Câu 14: B
Câu 15: Không có câu nào đúng
Đúng 0
Bình luận (0)
Giải chi tiết giúp e vs ạ
Các công thức lượng giác cơ bản liên quan đến góc của lớp 10:
\(sin\left(3\pi-x\right)=sin\left(2\pi+\pi-x\right)=sin\left(\pi-x\right)=sinx\)
\(sin\left(\dfrac{\pi}{2}+x\right)=cosx\Rightarrow sin\left(\dfrac{5\pi}{2}+x\right)=sin\left(2\pi+\dfrac{\pi}{2}+x\right)=sin\left(\dfrac{\pi}{2}+x\right)=cosx\)
\(cos\left(\dfrac{\pi}{2}+x\right)=-sinx\)
\(sin\left(\dfrac{3\pi}{2}+x\right)=sin\left(2\pi-\dfrac{\pi}{2}+x\right)=sin\left(-\dfrac{\pi}{2}+x\right)=-cosx\)
Nên pt tương đương:
\(3sin^2x-2sinx.cosx-5cos^2x=0\)
Với \(cosx=0\) không là nghiệm
Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)
\(\Rightarrow3tan^2x-2tanx-5=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=-1\\tanx=\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{5}{3}\right)+k\pi\end{matrix}\right.\)
Đúng 2
Bình luận (0)
















