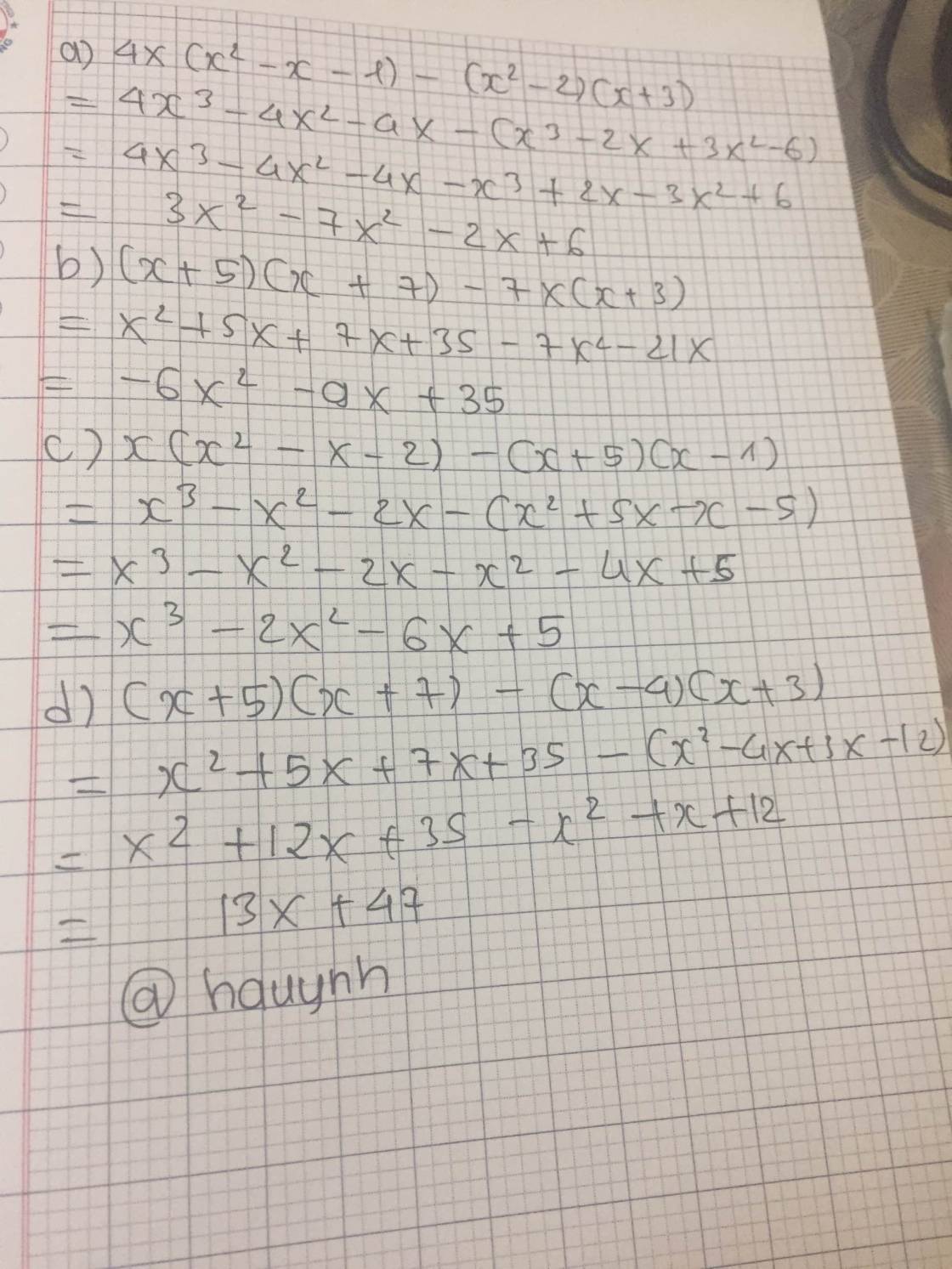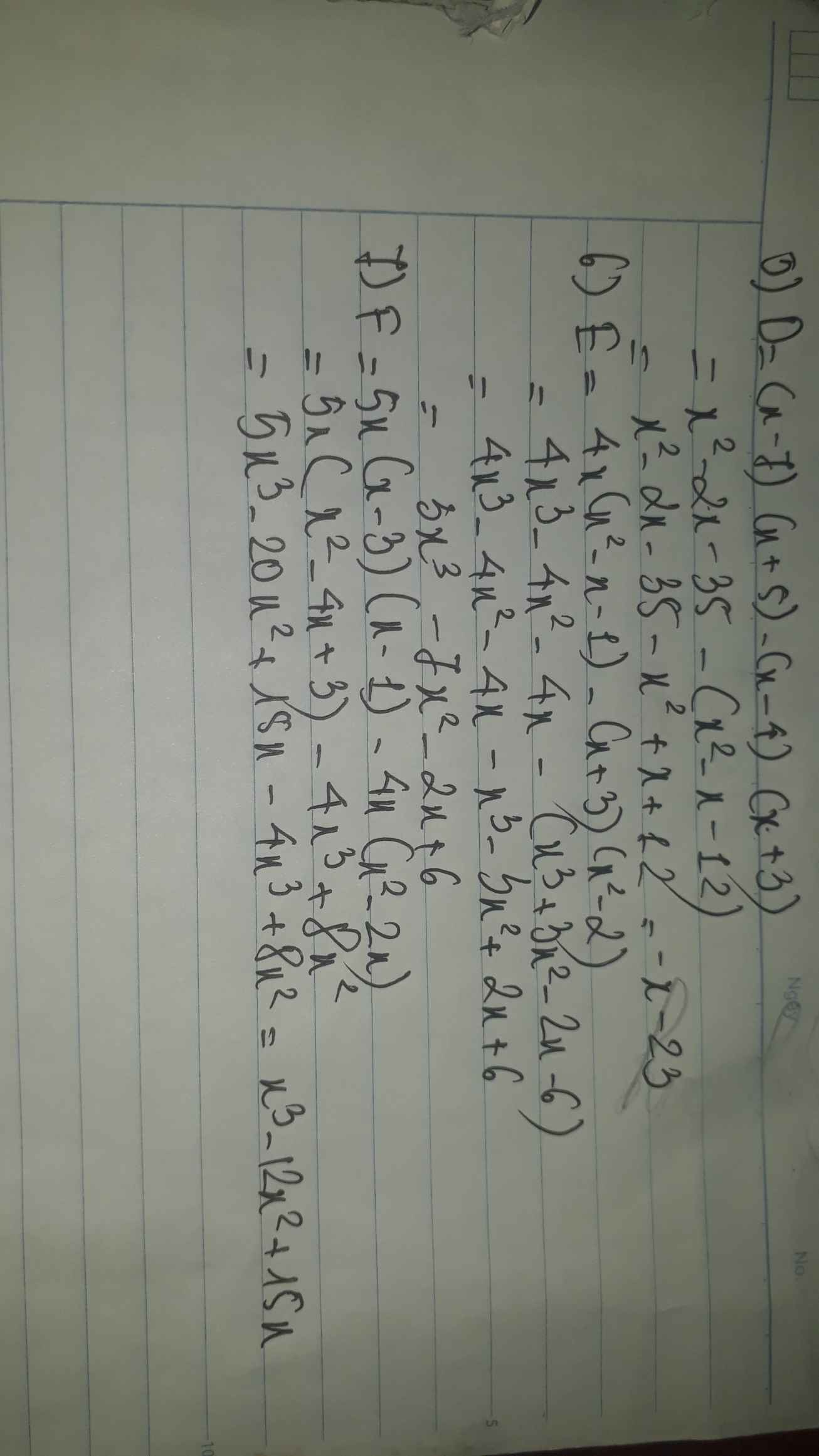y x ( 8 + 2 ) = 420

y x 10 = 420

y = 420 : 10

y = 42

y x ( 109 - 9 ) = 2300

y x 100 = 2300

y = 23

y x 8 +y x2 = 420

yx(8+2)=420

y          =420/(8+2)

y          =420/10

y         =  42

109 x y -9 x y = 2300

y x(109-9)       =2300

y                      =2300/(109-9)

y                       =2300/100

y                       =23

thank you 

*) 13 × 5 … 31 × 5

Hai phép tính trên có thừa số 5 giống nhau, vì 13 < 31 nên 13 × 5 < 31 × 5.

*) 502 × 6 … 500 × 6

Hai phép tính trên có thừa số 6 giống nhau, vì 502 > 500 nên 502 × 6 > 500 × 6

*) 240 × 3 … 420 × 3

Hai phép tính trên có thừa số 3 giống nhau, vì 240 < 420 nên 240 × 3 < 420 × 3.

*) 7 × 620 … 602 × 7

Hai phép tính trên có thừa số 7 giống nhau, vì 620 > 602 nên 7 × 620 > 602 × 7.

42x91+6x19x7-420

=42x91+(6x7)x19-420

=42x91+42x19-420

=42x(91+19)-420

=42x100-42x10

=42x(100-10)

=42x90

=3780

2)99x1001-99

=99x1001-99x1

=99x(1001-1)

=99x1000

=99000

\(12.\left(x+41\right)=624\)

\(\Leftrightarrow x+41=52\)

\(\Leftrightarrow x=11\)

\(420:\left(3x-6\right)=7\)

\(\Leftrightarrow3x-6=60\)

\(\Leftrightarrow3x=66\)

\(\Leftrightarrow x=22\)

12 . ( x + 41 ) = 624 

x + 41 = 624 : 12

x + 41 = 52

x         = 52 - 41 

x         =   11

420 : ( 3 . x-6 ) = 7

3 . x - 6 = 420 : 7

3 . x - 6  =   60

3 . x  = 60 + 6 

3 . x = 66

x  = 66 : 3

x  =   22

12.(X+41)=624

     (X+41)=624:12

      X       = 52-41

      X       = 11

420:(3.X-6)=7

       (3.X-6)=420:7

        3.X-6 = 60

        3.X    = 60-6

        3.X    = 54

           X    = 54:3

           X    = 18

a)

160 : (4 × 8) = 160 : 32 = 5

160 : 4 : 8 = 40 : 8 = 5

Vậy 160 : (4 × 8) = 160 : 4 : 8.

96 : (3 × 8) = 96 : 24 = 4

96 : 3 : 8 = 32 : 8 = 4

Vậy 96 : (3 × 8) = 96 : 3 : 8.

105 : (5 × 7) = 105 : 35 = 3

105 : 5 : 7 = 21 : 7 = 3

Vậy 105 : (5 × 7) = 105 : 5 : 7.

Nhận xét: a : (b × c) = a : b : c

b)

270 : (9 × 6) = 270 : 9 : 6 = 30 : 6 = 5

420 : (7 × 3) = 420 : 7 : 3 = 60 : 3 = 20

144 : (2 × 8) = 144 : 2 : 8 = 72 : 8 = 9

a) [ 25 - ( x + 1,85 ) ] : 3 = 7

[ 25 - ( x + 1,85) ] = 7x3

[ 25 - ( x + 1,85 ) ] = 21

x + 1,85= 25-21

x + 1,85= 4

x= 4-1,85

x= 2,15

a) [25 - (x + 1,85)] : 3 = 7

=> 25 - (x + 1,85)       = 3 x 7

=> 25 - (x + 1,85)       = 21

=> x + 1,85                 = 25 - 21

=> x + 1,85                  = 4

=> x                             = 4 - 1,85

=> x                             = 2,15

b) 420 : [75  - (x - 10)] = 21

=> 75 - (x - 10) = 420 : 21

=> 75 - (x - 10) = 20

=> x - 10           = 75 - 20

=> x - 10           = 55

 => x                  = 55 + 10

=> x                   = 65

b) 420 : [ 75 - ( x-10 ) ] = 21

[ 75 - ( x-10) ]= 420:21

[ 75 - ( x-10) ] = 20

( x- 10) =75-20

 x-10 = 55

x= 55+10

x=65

`@` `\text {dnammv}`

`a,`

`4x(x^2-x-1)-(x^2-2)(x+3)`

`= 4x^3-4x^2-4x- [x^2(x+3)-2(x+3)]`

`= 4x^3-4x^2-4x- (x^3+3x^2-2x-6)`
`= 4x^3-4x^2-4x-x^3-3x^2+2x+6`

`= 3x^3 - 7x^2-2x+6`

`b,`

`(x+5)(x+7)-7x(x+3)`

`= x(x+7)+5(x+7)-7x^2-21x`

`= x^2+7+5x+35-7x^2-21x`

`= -6x^2-16x+35`

`c,`

`x(x^2-x-2)-(x+5)(x-1)`

`= x^3-x^2-2x- [x(x-1)+5(x-1)]`

`= x^3-x^2-2x- (x^2-x+5x-5)`

`= x^3-x^2-2x - x^2 + x -5x+5`

`= x^3-2x^2- 4x+5`

`d,`

`(x+5)(x+7)-(x-4)(x+3)`

`= x(x+7)+5(x+7)- [x(x+3)-4(x+3)]`

`= x^2+7x+5x+35 - (x^2+3x-4x-12)`

`= x^2+12x+35 - x^2+x+12`

`= 13x+47`

a)

 ⇔ \(x^2-16=9\)

⇔ \(x^2=25\)

⇔ \(x=\pm5\)

b)

 ⇔ \(x^2-4x+4-25x^2+20x-4=0\)

⇔ \(16x-24x^2=0\)

⇔ \(8x\left(2-3x\right)=0\)

⇒ \(\left[{}\begin{matrix}x=0\\2-3x=0\end{matrix}\right.\)   ⇔   \(\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)

Vậy \(x=0\) hoặc \(x=\dfrac{2}{3}\)

c)  

⇔ \(3x^2-10x-20=0\)

⇔ \(x^2-2.x.\dfrac{5}{3}+\dfrac{25}{9}-\dfrac{205}{9}=0\)

⇔ \(\left(x-\dfrac{5}{3}\right)^2=\dfrac{205}{9}\)

⇒ \(\left[{}\begin{matrix}x-\dfrac{5}{3}=\sqrt{\dfrac{205}{9}}\\x-\dfrac{5}{3}=-\sqrt{\dfrac{205}{9}}\end{matrix}\right.\)  ⇔ \(\left[{}\begin{matrix}x=\dfrac{\sqrt{\text{205}}}{\text{3}}+\dfrac{5}{3}\\x=-\dfrac{\sqrt{\text{205}}}{\text{3}}+\dfrac{5}{3}\end{matrix}\right.\)  ⇔ \(\left[{}\begin{matrix}x=\dfrac{15+\text{9}\sqrt{\text{205}}}{\text{9}}\\\text{x}=-\dfrac{15+\text{9}\sqrt{\text{205}}}{\text{9}}\end{matrix}\right.\)

Vậy... 

d) 

⇔ \(\left(x^2+x\right)^2-49=\left(x^2+x\right)^2-7x\)

⇔ 7x = 49

⇔ x=7

Vậy...