Trình bày lời giải mấy câu này giúp em với ạ


Những câu hỏi liên quan
Trình bày lời giải mấy câu này giúp em với ạ!! Em xin cảm ơn.
Đọc tiếp
Trình bày lời giải mấy câu này giúp em với ạ!! Em xin cảm ơn.
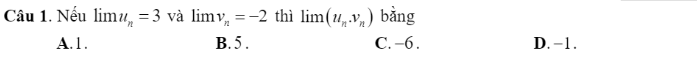



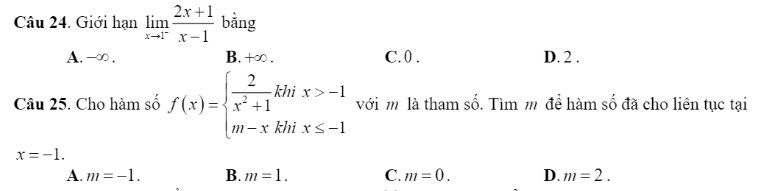

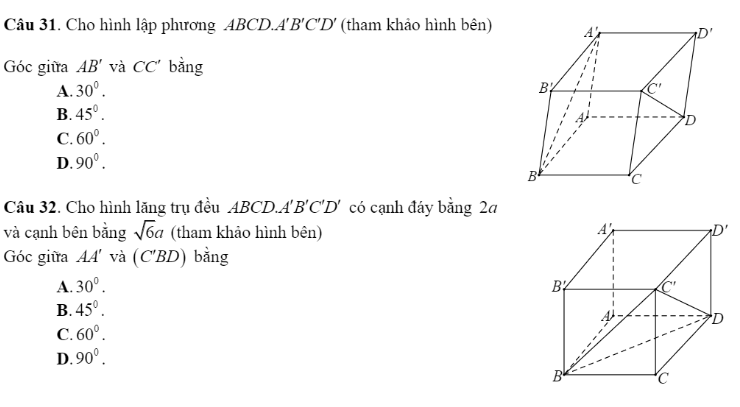
Mọi người trình bày cách giải mấy câu này giúp em với ạ!!
Đọc tiếp
Mọi người trình bày cách giải mấy câu này giúp em với ạ!!

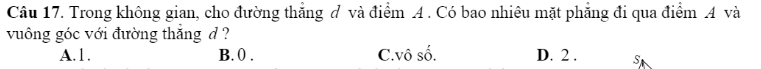
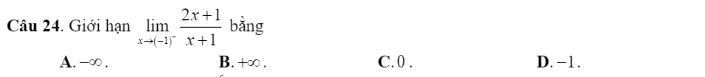

2.B (t/c của giới hạn)
6.B H/s ko x/đ với x = 0 -> Ko liên tục tại đ x = 0
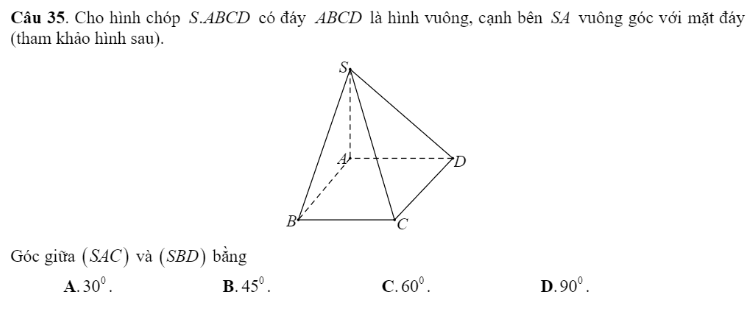
17.C
24. \(\lim\limits_{x\rightarrow\left(-1\right)^-}\dfrac{2x+1}{x+1}\) . Thấy : \(\lim\limits_{x\rightarrow\left(-1\right)^-}2x+1=2.\left(-1\right)+1=-1\)
\(\lim\limits_{x\rightarrow\left(-1\right)^-}x+1=0\) ; \(x\rightarrow\left(-1\right)^-\Rightarrow x+1< 0\).
Do đó : \(\lim\limits_{x\rightarrow\left(-1\right)^-}=+\infty\) . Chọn B
Đúng 3
Bình luận (0)
33 . B
Trên (SAB) ; Lấy H là TĐ của AB ; ta có : SH \(\perp AB\) ( \(\Delta SAB\) đều ) ; HC \(\perp AB\) ( \(\Delta ABC\) đều )
Ta có : (SAB) \(\perp\left(ABC\right)\) ; \(\left(SAB\right)\cap\left(ABC\right)=AB;SH\perp AB\)
\(\Rightarrow SH\perp\left(ABC\right)\)
\(SC\cap\left(ABC\right)=C\) . Suy ra : \(\left(SC;\left(ABC\right)\right)=\widehat{SCH}\)
Có : \(SH\perp HC\) => \(\Delta SHC\) vuông tại H
G/s \(\Delta\)ABC đều có cạnh là a \(\Rightarrow AB=a\)
\(\Delta SAB\) đều => SA = SB = AB = a
Tính được : \(SH=HC=\dfrac{\sqrt{3}}{2}a\)
\(\Delta SHC\) vuông tại H : \(tan\widehat{SCH}=\dfrac{SH}{HC}=1\)
\(\Rightarrow\widehat{SCH}=45^o\) => ...
Đúng 3
Bình luận (0)
Trình bày cách giải mấy câu này giúp mình với ạ :((( khó quá


15.
\(\Delta'=m^2+m-2>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\)
Đáp án B
16.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow\dfrac{\pi}{4}< \dfrac{a}{2}< \dfrac{\pi}{2}\Rightarrow\dfrac{\sqrt{2}}{2}< sin\dfrac{a}{2}< 1\Rightarrow\dfrac{1}{2}< sin^2\dfrac{a}{2}< 1\)
\(sina=\dfrac{3}{5}\Leftrightarrow sin^2a=\dfrac{9}{25}\Leftrightarrow4sin^2\dfrac{a}{2}.cos^2\dfrac{a}{2}=\dfrac{9}{25}\)
\(\Leftrightarrow sin^2\dfrac{a}{2}\left(1-sin^2\dfrac{a}{2}\right)=\dfrac{9}{100}\Leftrightarrow sin^4\dfrac{a}{2}-sin^2\dfrac{a}{2}+\dfrac{9}{100}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2\dfrac{a}{2}=\dfrac{1}{10}< \dfrac{1}{2}\left(loại\right)\\sin^2\dfrac{a}{2}=\dfrac{9}{10}\end{matrix}\right.\)
\(\Rightarrow sin\dfrac{a}{2}=\dfrac{3\sqrt{10}}{10}\)
Đúng 3
Bình luận (0)
17.
Áp dụng công thức trung tuyến:
\(AM=\dfrac{\sqrt{2\left(AB^2+AC^2\right)-BC^2}}{2}=\dfrac{\sqrt{201}}{2}\)
18.
\(\Leftrightarrow x^2+2x+4>m^2+2m\) ; \(\forall x\in\left[-2;1\right]\)
\(\Leftrightarrow m^2+2m< \min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)\)
Xét \(f\left(x\right)=x^2+2x+4\) trên \(\left[-2;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-2;1\right]\) ; \(f\left(-2\right)=4\) ; \(f\left(-1\right)=3\) ; \(f\left(1\right)=7\)
\(\Rightarrow\min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)=f\left(1\right)=3\)
\(\Rightarrow m^2+2m< 3\Leftrightarrow m^2+2m-3< 0\)
\(\Rightarrow-3< m< 1\Rightarrow m=\left\{-2;-1;0\right\}\)
Đáp án C
Đúng 3
Bình luận (0)
19. Hình đa giác là bát giác đều như hình vẽ

\(S=8S_{OAB}=8.\dfrac{1}{2}.IB.OA=4.y_B.x_A=4.\dfrac{\sqrt{2}}{2}.1=2\sqrt{2}\)
Cả 4 đáp án đều không chính xác?
20.
\(M\in\Delta\Rightarrow a+b+1=0\Rightarrow b=-a-1\Rightarrow M\left(a;-a-1\right)\)
\(\left\{{}\begin{matrix}\overrightarrow{AM}=\left(a+1;-a-4\right)\\\overrightarrow{BM}=\left(a-1;-a-2\right)\end{matrix}\right.\)
\(AM+BM=\sqrt{\left(a+1\right)^2+\left(-a-4\right)^2}+\sqrt{\left(-a-2\right)^2+\left(a-1\right)^2}\)
\(AM+BM\ge\sqrt{\left(a+1-a-2\right)^2+\left(-a-4+a-1\right)^2}=\sqrt{26}\)
Dấu "=" xảy ra khi:
\(\left(a+1\right)\left(a-1\right)=\left(-a-4\right)\left(-a-2\right)\Leftrightarrow a=-\dfrac{3}{2}\Rightarrow b=\dfrac{1}{2}\)
\(\Rightarrow ab=-\dfrac{3}{4}\)
Đúng 3
Bình luận (5)
lần này không phải chữa đề mà là giải đề ạ :(( mấy câu cuối của đề toán lúc nào cũng là vấn đề đối với mấy đứa tệ toán như em . Mong mọi người giúp đỡ và trình bày cách giải ạ

17.
\(f\left(x\right)>0;\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1>0\left(luôn-đúng\right)\\\Delta'=\left(2m-1\right)^2-\left(3m^2-2m+4\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow m^2-2m-3< 0\)
\(\Leftrightarrow-1< m< 3\)
\(\Rightarrow m=\left\{0;1;2\right\}\)
18.
\(\pi< x< \dfrac{3\pi}{2}\Rightarrow cosx< 0\)
\(\Rightarrow cosx=-\sqrt{1-sin^2x}=-\dfrac{\sqrt{5}}{3}\)
\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\dfrac{2\sqrt{5}}{5}\)
\(tan\left(x+\dfrac{\pi}{4}\right)=\dfrac{tanx+tan\dfrac{\pi}{4}}{1-tanx.tan\dfrac{\pi}{4}}=\dfrac{\dfrac{2\sqrt{5}}{5}+1}{1-\dfrac{2\sqrt{5}}{5}.1}=9+4\sqrt{5}\)
Đúng 1
Bình luận (0)
19.
\(a^2=b^2+c^2+bc\Rightarrow b^2+c^2-a^2=-bc\)
\(\Rightarrow cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{-bc}{2bc}=-\dfrac{1}{2}\)
\(\Rightarrow A=120^0\)
20.
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\)
\(d\left(I;\Delta\right)=\dfrac{\left|2-1-3\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\)
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}IH=d\left(I;\Delta\right)\\AH=\dfrac{1}{2}AB\end{matrix}\right.\)
Áp dụng định lý Pitago trong tam giác vuông IAH:
\(IA^2=IH^2+AH^2\Leftrightarrow R^2=IH^2+AH^2\)
\(\Rightarrow AH=\sqrt{2}\Rightarrow AB=2AH=2\sqrt{2}\)
Đúng 1
Bình luận (0)
21.
\(2x^2-\left(m+1\right)x+3m-15\le0\)
\(\Leftrightarrow2x^2-x-15-m\left(x-3\right)\le0\)
\(\Leftrightarrow\left(x-3\right)\left(2x+5\right)-m\left(x-3\right)\le0\)
\(\Leftrightarrow\left(x-3\right)\left(2x+5-m\right)\le0\)
Do \(x\in\left[1;2\right]\Rightarrow x-3< 0\) nên BPT tương đương:
\(2x+5-m\ge0\)
\(\Leftrightarrow2x+5\ge m\)
BPT đúng với mọi \(x\in\left[1;2\right]\) khi và chỉ khi: \(m\le7\)
\(\Rightarrow m=\left\{1;2;3;4;5;6;7\right\}\)
Cả 4 đáp án đều sai?
P/s: đã thử lại, chỉ có 7 giá trị nguyên dương là đáp án đúng
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Chuyện mục chữa đề ạ. Gần thi nên em có khá nhiều bài tập , mong mọi người chữa+ trình bày cách giải của mấy câu sai(và mấy câu em không biết làm) giúp em với ạ:((


12 sai, C mới là đáp án đúng
13 sai, A đúng, \(sin-sin=2cos...sin...\)
18.
\(\Leftrightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=m^2-m\left(-m+3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m^2-3m< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>0\\0< m< \dfrac{3}{2}\end{matrix}\right.\) \(\Rightarrow m=1\)
Đáp án B
22.
Để pt có 2 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\-m^2+4m-3>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\1< m< 3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2\left(2m-3\right)}{m-2}\\x_1x_2=\dfrac{5m-6}{m-2}\end{matrix}\right.\)
\(\dfrac{-2\left(2m-3\right)}{m-2}+\dfrac{5m-6}{m-2}\le0\)
\(\Leftrightarrow\dfrac{m}{m-2}\le0\) \(\Leftrightarrow0\le m< 2\)
Kết hợp điều kiện delta \(\Rightarrow1< m< 2\)
Đúng 2
Bình luận (0)
24.
Đề bài câu này dính lỗi, ko có điểm M nào cả, chắc là đường thẳng đi qua A
Đường tròn (C) tâm I(1;-2) bán kính R=4
\(\overrightarrow{IA}=\left(1;3\right)\)
Gọi d là đường thẳng qua A và cắt (C) tại 2 điểm B và C. Gọi H là trung điểm BC
\(\Rightarrow IH\perp BC\Rightarrow IH=d\left(I;d\right)\)
Theo định lý đường xiên - đường vuông góc ta luôn có: \(IH\le IA\)
Áp dụng Pitago cho tam giác vuông IBH:
\(BH=\sqrt{IB^2-IH^2}\Leftrightarrow\dfrac{BC}{2}=\sqrt{16-IH^2}\)
\(\Rightarrow BC_{min}\) khi \(IH_{max}\Leftrightarrow IH=IA\)
\(\Leftrightarrow IA\perp d\Rightarrow d\) nhận \(\overrightarrow{IA}\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)+3\left(y-1\right)=0\Leftrightarrow x+3y-5=0\)
Đúng 2
Bình luận (0)
#chuyên mục chữa đề
Vẫn là mong được giúp đỡ, câu sai (và mấy câu chưa làm được) thì trình bày cách giải giúp em với ạ


#chuyên mục chữa đề
mong mọi người trình bày cách giải của mấy câu sai giúp em ạ :((( đề khó quá


11.
\(tan\left(x-\pi\right)=-tan\left(\pi-x\right)=tanx\)
Đúng 1
Bình luận (0)
12.
\(sinx+sin3x=2sin\dfrac{x+3x}{2}.cos\dfrac{x-3x}{2}=2sin2x.cos\left(-x\right)=2sin2x.cosx\)
Đúng 1
Bình luận (0)
15.
\(x^2+y^2-2x+4y-4=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=9\)
\(\Rightarrow\) Tâm \(I=\left(1;-2\right)\), bán kính \(R=3\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Bạn nào giải giúp mình hai câu này vs ạ , trình bày hộ mình với , mình cám ơn ạ
22/ \(\omega A=8\pi\)
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Leftrightarrow A^2=3,2^2+\dfrac{\left(4,8\pi\right)^2}{\omega^2}\)
\(\Leftrightarrow\omega^2A^2=3,2^2\omega^2+23,04\pi^2\Leftrightarrow64\pi^2=3,2^2.\omega^2+23,04\pi^2\Leftrightarrow\omega=2\pi\left(rad/s\right)\)
\(\Rightarrow f=\dfrac{\omega}{2\pi}=\dfrac{2\pi}{2\pi}=1\left(Hz\right)\Rightarrow D.1Hz\)
23/ \(\omega A=20;\omega^2A=80\Rightarrow\left\{{}\begin{matrix}\omega=4\left(rad/s\right)\\A=5cm\end{matrix}\right.\)
\(\Rightarrow v=\omega\sqrt{A^2-x^2}=4.\sqrt{5^2-4^2}=12\left(cm/s\right)\Rightarrow A.12cm/s\)
Đúng 1
Bình luận (0)
làm giúp em đề hoá này với ạ và câu 31 32 trình bày tự luận hộ em em cảm ơn















