Phân tích đa thức sau thành nhân tử:
a10 + a5 + 1
Phân tích các đa thức sau thành nhân tử:
a) 27 x 3 - 54 x 2 y + 36 xy 2 - 8 y 3 ; b) x 3 - 1 + 5 x 2 -5+3x - 3;
c) a 5 +a 4 +a 3 +a 2 +a + 1.
a) ( 3 x - 2 y ) 3 . b) ( x - 1 ) ( x + 3 ) 2 .
 phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hạng tử)
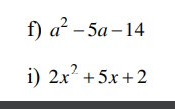 phân tích đa thức sau thành nhân tử(tách 1 hạng tử
phân tích đa thức sau thành nhân tử(tách 1 hạng tử
thành nhiều hạng tử
f, \(a^2-5a+14\) không phân tích được thành nhân tử.
i, \(2x^2+5x+2=2x^2+4x+x+2=2x\left(x+2\right)+\left(x+2\right)=\left(x+2\right)\left(2x+1\right)\)
1 a. phân tích đa thức -x3 + 3x2 - 3x + 1 thành nhân tử
b. phân tích đa thức 1 - 3x + 3x2 - x3 thành nhân tử
1a) \(=-\left(x^3-3x^2+3x-1\right)=-\left(x-1\right)^3\)
b) \(=-\left(x^3-3x^2+3x-1\right)=-\left(x-1\right)^3\)
\(a,=-\left(x-1\right)^3\left[=\left(1-x\right)^3\right]\\ b,=\left(1-x\right)^3\)
a. \(=-\left(x^3-3x^2+3x-1\right)=-\left(x-1\right)^3\)
b. \(=\left(1-x\right)^3\)
 phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hangj tử(kè công thức dùm )
phân tích đa thức sau thành nhân tử(tách 1 hạng tử thành nhiều hangj tử(kè công thức dùm )
g) `2m^2+10m+8`
`=(2m^2+2m)+(8m+8)`
`=2m(m+1)+8(m+1)`
`=(m+1)(2m+8)`
f) `4p^2-36p+56`
`=(4p^2-8p)-(28p-56)`
`=4p(p-2)-14(p-2)`
`=(p-2)(4p-14)`
Bài 1 : Phân tích các đa thức sau thành nhân tử :
1) 15x + 15y 2) 8x - 12y
3) xy - x 4) 4x^2- 6x
Bài 2 : Phân tích các đa thức sau thành nhân tử :
1) 2(x + y) - 5a(x + y) 2) a^2(x - 5) - 3(x - 5)
3) 4x(a - b) + 6xy(a - b) 4) 3x(x - 1) + 5(x -1)
Bài 3 : Tính giá trị của biểu thức :
1) A = 13.87 + 13.12 + 13
2) B = (x - 3).2x + (x - 3).y tại x = 13 và y = 4
Bài 4 : Tìm x :
1) x(x - 5) - 2(x - 5) = 0 2) 3x(x - 4) - x + 4 = 0
3) x(x - 7) - 2(7 - x) = 0 4) 2x(2x + 3) - 2x - 3 = 0
\(1,\\ 1,=15\left(x+y\right)\\ 2,=4\left(2x-3y\right)\\ 3,=x\left(y-1\right)\\ 4,=2x\left(2x-3\right)\\ 2,\\ 1,=\left(x+y\right)\left(2-5a\right)\\ 2,=\left(x-5\right)\left(a^2-3\right)\\ 3,=\left(a-b\right)\left(4x+6xy\right)=2x\left(2+3y\right)\left(a-b\right)\\ 4,=\left(x-1\right)\left(3x+5\right)\\ 3,\\ A=13\left(87+12+1\right)=13\cdot100=1300\\ B=\left(x-3\right)\left(2x+y\right)=\left(13-3\right)\left(26+4\right)=10\cdot30=300\\ 4,\\ 1,\Rightarrow\left(x-5\right)\left(x-2\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\\ 2,\Rightarrow\left(x-7\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ 3,\Rightarrow\left(3x-1\right)\left(x-4\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=4\end{matrix}\right.\\ 4,\Rightarrow\left(2x+3\right)\left(2x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Phân tích đa thức thành nhân tử -8 - Phân tích đa thức thành nhân tử -8 x mũ 3 cộng 1 ta được
\(-8x^3+1=1^3-\left(2x\right)^3=\left(1-2x\right)\left(1+2x+4x^2\right)\)
Phân tích đa thức sau thành nhân tử 9 x 2 - 1
Ta có: 9 x 2 - 1 = ( 3 x ) 2 - 1 2 = ( 3 x - 1 ) ( 3 x + 1 )
Phân tích đa thức sau thành nhân tử 9 x 2 - 1
Ta có: 9 x 2 - 1 = ( 3 x ) 2 - 1 2 = ( 3 x - 1 ) ( 3 x + 1 )
Bài 1: Phân tích các đa thức sau thành nhân tử
HD: Dùng phương pháp đặt nhân tử chung phối hợp dùng hằng đẳng thức số 1, 2
1) x3 – 2x – x 2) 6x2 + 12xy + 6y2
3) 2y3 + 8y3 + 8y 4) 5x2 – 10xy + 5y2
Bài 2: Phân tích các đa thức sau thành nhân tử
HD: Dùng pp đặt nhân tử chung phối hợp dùng hằng đẳng thức số 3, 6, 7
1) x3 – 64x 2) 8x2y – 18y 3) 24x3 – 3
Bài 3: Phân tích các đa thức sau thành nhân tử
HD: Dùng phương pháp nhóm hạng tử phối hợp dùng hằng đẳng thức
1) 5x2 + 10x + 5 – 5y2 2) 3x3 – 6x2 + 3x – 12xy2
3) a3b – ab3 + a2 + 2ab + b2 4) 2x3 – 2xy2 – 8x2 + 8xy
Giup mik với mik cần gấp lắm!
Bài 1:
\(1,Sửa:x^3-2x^2+x=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
\(1,=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\\ 2,=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\\ 3,=3\left(x^3-1\right)=3\left(x-1\right)\left(x^2+x+1\right)\)
Bài 3:
\(a,=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y^2\right]=5\left(x-y+1\right)\left(x+y+1\right)\\ b,=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-4y^2\right]\\ =3x\left(x-2y-1\right)\left(x+2y-1\right)\\ c,=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2\\ =\left(a+b\right)\left(a^2b-ab^2+a+b\right)\\ d,=2x\left(x^2-y^2-4x+4\right)=2x\left[\left(x-2\right)^2-y^2\right]\\ =2x\left(x-y-2\right)\left(x+y-2\right)\)
Bài 1;
1) \(x^3-2x-x=x\left(x^2-2x-1\right)\)
2) \(6x^2+12xy+6y^2=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\)
3) \(2y^3+8y^3+8y=10y^3+8y=2y\left(5y^2+4\right)\)
4) \(5x^2-10xy+5y^2=5\left(x^2-2xy+y^2\right)=5\left(x-y\right)^2\)
Bài 2:
1) \(x^3-64x=x\left(x^2-64\right)=x\left(x-8\right)\left(x+8\right)\)
2) \(8x^2y-18y=2y\left(4x^2-9\right)=2y\left(2x-3\right)\left(2x+3\right)\)
3) \(24x^3-3=3\left(8x^3-1\right)=3\left(2x-1\right)\left(4x^2+2x+1\right)\)
Bài 3:
1) \(5x^2+10x+5-5y^2=5\left(x^2+2x+1-y^2\right)=5\left[\left(x+1\right)^2-y\right]=5\left(x-y+1\right)\left(x+y+1\right)\)
2) \(3x^3-6x^2+3x-12xy^2=3x\left(x^2-2x+1-4y^2\right)=3x\left[\left(x-1\right)^2-\left(2y\right)^2\right]=3x\left(x-2y-1\right)\left(x+2y-1\right)\)
3) \(a^3b-ab^3+a^2+2ab+b^2=ab\left(a^2-b^2\right)+\left(a+b\right)^2=ab\left(a-b\right)\left(a+b\right)+\left(a+b\right)^2=\left(a+b\right)\left(a^2b-ab^2+a+b\right)\)
4) \(2x^3-2xy^2-8x^2+8xy=2x\left(x^2-y^2-4x+4y\right)=2x\left[\left(x-y\right)\left(x+y\right)-4\left(x-y\right)\right]=2x\left(x-y\right)\left(x+y-4\right)\)