
Làm hộ em câu 9 bài hình thôi ạ Nguyễn Việt Lâm Giáo viên
Làm hộ em bài 11 Chỉ cần làm câu c d thôi ạ🥺
Bài 12:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Thầy Nguyễn Việt Lâm ơi giúp em mấy bài này với.Em sắp phải nộp rồi ạ 

4.
\(ab+bc+ca=3abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)
Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
\(S=\sum\dfrac{\dfrac{1}{y^2}}{\dfrac{1}{x}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)}=\sum\dfrac{x^3}{x^2+y^2}=\sum\left(x-\dfrac{xy^2}{x^2+y^2}\right)\)
\(S\ge\sum\left(x-\dfrac{xy^2}{2xy}\right)=\sum\left(x-\dfrac{y}{2}\right)=\dfrac{x+y+z}{2}=\dfrac{3}{2}\)
\(S_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
5.
Đặt \(\left(\dfrac{1}{a};\dfrac{2}{b};\dfrac{3}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
Đặt vế trái là P
\(P=\dfrac{z^3}{x^2+z^2}+\dfrac{x^3}{x^2+y^2}+\dfrac{y^3}{y^2+z^2}\)
Quay lại dòng 3 của bài số 4
6.
Do a;b;c không âm, ta có:
\(b^2\left(b-1\right)^2\left(b+2\right)\ge0\)
\(\Leftrightarrow b^5-3b^3+2b^2\ge0\)
\(\Leftrightarrow b^5-3b^3+2b^2-6\ge-6\)
\(\Leftrightarrow-\left(3-b^2\right)\left(b^3+2\right)\ge-6\)
\(\Leftrightarrow6\ge\left(3-b^2\right)\left(b^3+2\right)\)
\(\Rightarrow\dfrac{1}{b^3+2}\ge\dfrac{3-b^2}{6}\)
\(\Rightarrow\dfrac{a}{b^3+2}\ge\dfrac{a\left(3-b^2\right)}{6}\)
Tương tự: \(\dfrac{b}{c^3+2}\ge\dfrac{b\left(3-c^2\right)}{6}\) ; \(\dfrac{c}{a^3+2}\ge\dfrac{c\left(3-a^2\right)}{6}\)
Cộng vế: \(P\ge\dfrac{a+b+c}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}=\dfrac{3}{2}-\dfrac{ab^2+bc^2+ca^2+abc}{6}\)
Không mất tính tổng quát, giả sử \(b=mid\left\{a;b;c\right\}\)
\(\left(b-a\right)\left(b-c\right)\le0\)
\(\Leftrightarrow b^2+ac\le ab+bc\)
\(\Leftrightarrow ab^2+ca^2\le a^2b+abc\)
\(\Rightarrow ab^2+bc^2+ca^2+abc\le bc^2+a^2b+2abc=b\left(a+c\right)^2=4b\left(\dfrac{a+c}{2}\right)\left(\dfrac{a+c}{2}\right)\le\dfrac{4}{27}\left(a+b+c\right)^3=4\)
\(\Rightarrow P\ge\dfrac{3}{2}-\dfrac{4}{6}=\dfrac{5}{6}\)

Trải qua 5 ngày thông báo về cuộc thi, HOC24 đã nhận được khá nhiều bài viết hay từ các thành viên. Rất nhiều tình cảm dành cho các bà, các mẹ, các cô giáo,... đã được gửi gắm.
Và qua ý kiến góp ý của thầy Nguyễn Việt Lâm, HOC24 xin cập nhật về hình thức bài dự thi. Bài dự thi có thể mang hình thức tự do (thơ, truyện ngắn, tản văn, nhật kí, thư...). Như vậy các bạn có thể bày tỏ tình cảm với người thân yêu của mình qua nhiều hình thức khác nhau.
Các bạn hãy gửi thật nhiều bài viết hay về HOC24 để vừa là dịp tri ân người phụ nữ quan trọng trong cuộc đời mình, và vừa có cơ hội nhận được những phần quà hấp dẫn nhé!
--------------------------------------------------------------------------------------------------------------
I. MỤC ĐÍCH TỔ CHỨC
Sự kiện nhằm tôn vinh và chúc mừng Ngày Quốc tế Phụ nữ, cũng là dịp để mọi người tri ân những người phụ nữ xung quanh bằng những câu từ đậm chất văn.
II. THÔNG TIN CUỘC THI
* Đối tượng tham gia: các bạn học sinh trong cộng đồng Hoc24.vn
* Nội dung cuộc thi: Viết về một người phụ nữ có ý nghĩa quan trọng trong cuộc đời em.
* Hình thức làm bài:
- Đánh máy
- Viết tay (khuyến khích trang trí thêm cho đẹp) và chụp hình tải lên.
Sau đó gửi Bài dự thi + Họ Tên + Link trang cá nhân hoc24 về mail: hoc24.cfs@gmail.com
Những bài viết hay sẽ được chia sẻ lên trang chủ HOC24.VN.
III. THỜI GIAN TỔ CHỨC
* 24/02/2023: thông báo tổ chức cuộc thi và chính thức nhận bài làm
* 05/03/2023: kết thúc nhận bài thi
* 08/03/2023: thông báo kết quả cuộc thi
Bài thi sẽ được chấm song song với thời gian thi cho đến ngày 07/03/2023.
IV. LƯU Ý KHI LÀM BÀI
* Tránh lạc đề và tuyệt đối không copy.
* Ngoài nội dung bài viết, BTC cũng rất chú ý đến điểm chính tả, không ghi tắt hay ký hiệu, không sử dụng teencode, dấu câu cần đặt đúng chỗ, tách đoạn tách dòng hợp lý, viết hoa đúng.
* Đối với bài thi viết tay phải trình bày rõ ràng, sạch đẹp, khi chụp hình gửi thì cần đảm bảo hình ảnh rõ ràng, ngay ngắn, không bị mờ (chữ đẹp, trình bày bắt mắt cũng là một lợi thế nha).
V. GIẢI THƯỞNG
01 giải nhất: 150 coin
01 giải nhì: 100 coin
01 giải ba: 70 coin
02 Giải khuyến khích: 50 coin
Ngoài ra, mọi bài thi hợp lệ đều sẽ nhận được phần thưởng khích lệ là 5 GP.
Các bạn gửi Bài dự thi + Họ Tên + Link trang cá nhân hoc24 về mail: hoc24.cfs@gmail.com nhé!
Ô! Thế thì hay quá, cuối cùng thì cũng có thể viết thư :3
Nói chung BTC chỉ đưa ra hình thức trình bày chứ không có đưa ra thể loại dự thi đúng không? Mình có thể viết thư, làm thơ, tản văn cũng có thể làm truyện ngắn, làm chương hồi,...đúng không nà?
Bài 2 ạ, em cần gấp lắm giáo viên giải hộ em nhanh chút được không ạ? Em cám ơnnn
thầy nguyễn việt lâm giúp em với ạ

5.
\(\sqrt{\left(a+b\right)\left(c+a\right)}\ge\sqrt{\left(\sqrt{ac}+\sqrt{ab}\right)^2}=\sqrt{ac}+\sqrt{ab}\)
\(\Rightarrow\dfrac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\le\dfrac{a}{a+\sqrt{ac}+\sqrt{ab}}=\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Tương tự:
\(\dfrac{b}{b+\sqrt{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
\(\dfrac{c}{c+\sqrt{\left(a+c\right)\left(b+c\right)}}\le\dfrac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Cộng vế với vế:
\(P\le\dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1\)
Dấu "=" xảy ra khi \(a=b=c\)
6.
\(P=\dfrac{a}{1+b-a}+\dfrac{b}{1+c-b}+\dfrac{c}{1+a-c}\)
Thay \(1=a+b+c\)
\(\Rightarrow P=\dfrac{a}{2b+c}+\dfrac{b}{2c+a}+\dfrac{c}{2a+b}\)
\(P=\dfrac{a^2}{2ab+ac}+\dfrac{b^2}{2bc+ab}+\dfrac{c^2}{2ac+bc}\)
\(P\ge\dfrac{\left(a+b+c\right)^2}{3ab+3bc+3ca}\ge\dfrac{3\left(ab+bc+ca\right)}{3\left(ab+bc+ca\right)}=1\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
7.
\(T=\left(x^2\right)^2+\left(y^2\right)^2+\left(z^2\right)^2\ge\dfrac{1}{3}\left(x^2+y^2+z^2\right)^2\)
\(T\ge\dfrac{1}{3}\left(xy+yz+zx\right)^2=\dfrac{1}{3}\)
\(T_{min}=\dfrac{1}{3}\) khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)
Thầy Nguyễn Việt Lâm giúp em với ạ
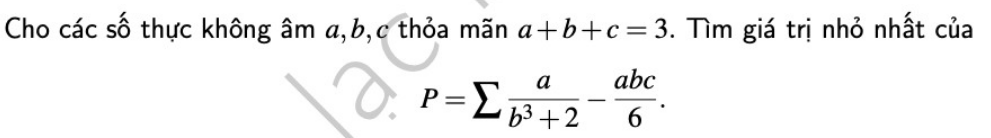
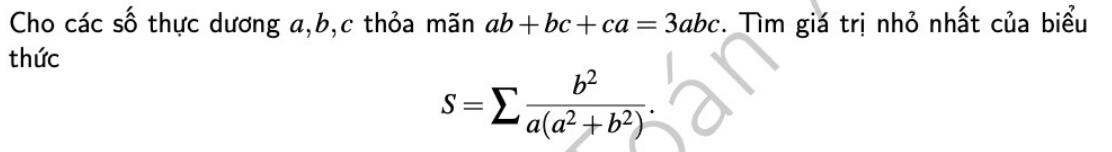
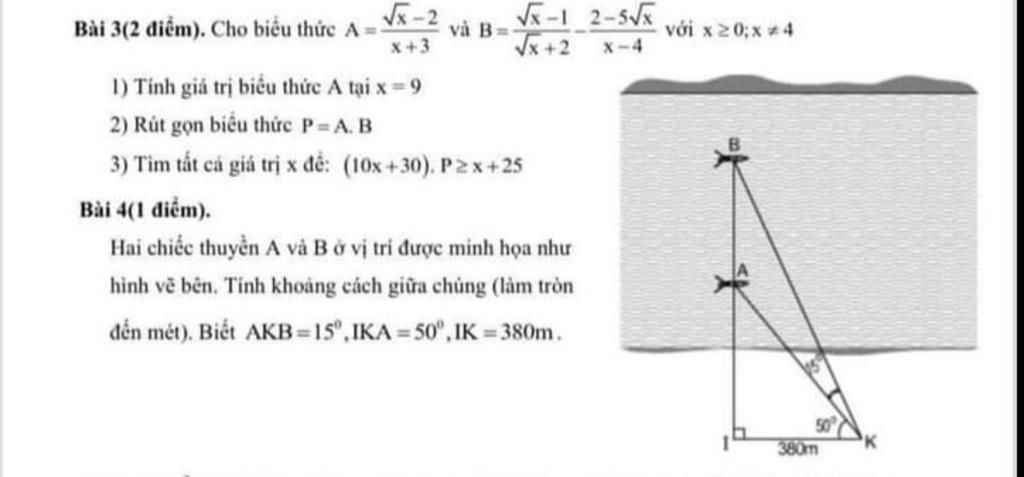
làm hộ em bài 3 thôi ạ
Bài 3:
a: Thay x=9 vào A, ta được:
\(A=\dfrac{3-2}{3+3}=\dfrac{1}{6}\)
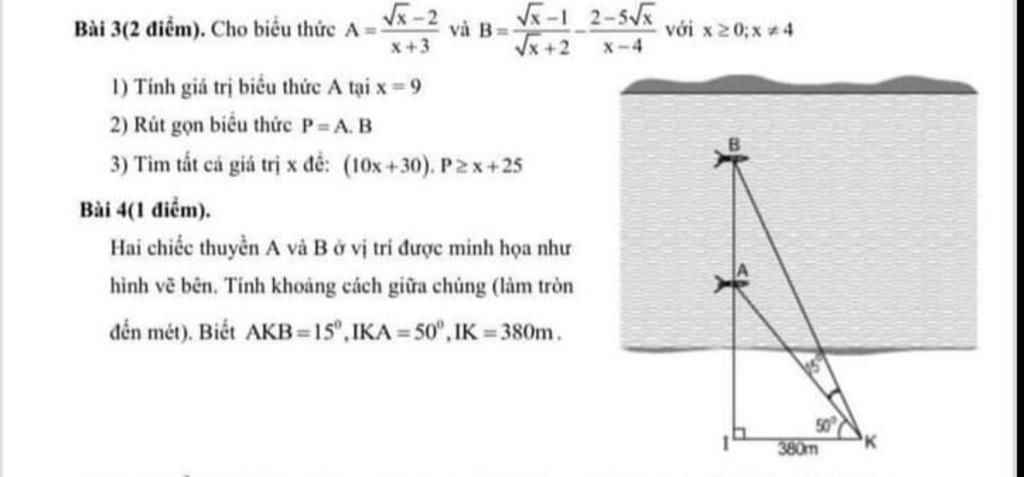
làm hộ em bài 1 thôi ạ
Bài 3:
\(1,x=9\Leftrightarrow A=\dfrac{3-2}{9+3}=\dfrac{1}{12}\\ 2,P=AB=\dfrac{\sqrt{x}-2}{x+3}\cdot\dfrac{x-3\sqrt{x}+2-2+5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(x+3\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{x+3}\\ 3,\left(10x+30\right)P\ge x+25\\ \Leftrightarrow\dfrac{3\sqrt{x}\left(x+3\right)}{x+3}-x-25\ge0\\ \Leftrightarrow3\sqrt{x}-x-25\ge0\\ \Leftrightarrow-\left(x-3\sqrt{x}+\dfrac{9}{4}\right)-\dfrac{91}{4}\ge0\\ \Leftrightarrow-\left(\sqrt{x}-\dfrac{3}{2}\right)^2-\dfrac{91}{4}\ge0\left(vô.lí\right)\\ \Leftrightarrow x\in\varnothing\)
làm hộ em bài 1 vs bài 2 thôi ạ

1)
a) 4y2-4xy+x2= x2-4xy+4y2= (x-2y)2
b) 9x2-12xy+4y2= (3x)2-2.3x.2y+(2y)2= (3x-2y)2
c) 16x2-25=(4x)2-52= (4x-5)(4x+5)
d) 1-9y2= 12-(3y)2=(1-3y)(1+3y)
g) x3-27y3= (x-3y)(x2+3xy+9y2)
h) 64 + 8x3=(4+2x)(16+8x+4x2)
i) x4+4y4-4x2y2= (x2)2-2x22y2+(y2)2=(x2-y2)2