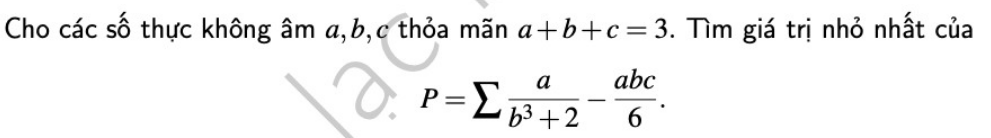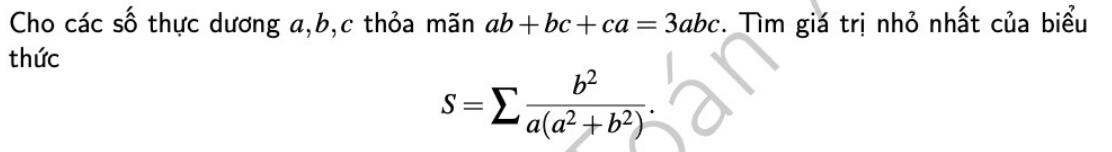5.
\(\sqrt{\left(a+b\right)\left(c+a\right)}\ge\sqrt{\left(\sqrt{ac}+\sqrt{ab}\right)^2}=\sqrt{ac}+\sqrt{ab}\)
\(\Rightarrow\dfrac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\le\dfrac{a}{a+\sqrt{ac}+\sqrt{ab}}=\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Tương tự:
\(\dfrac{b}{b+\sqrt{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
\(\dfrac{c}{c+\sqrt{\left(a+c\right)\left(b+c\right)}}\le\dfrac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Cộng vế với vế:
\(P\le\dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1\)
Dấu "=" xảy ra khi \(a=b=c\)
6.
\(P=\dfrac{a}{1+b-a}+\dfrac{b}{1+c-b}+\dfrac{c}{1+a-c}\)
Thay \(1=a+b+c\)
\(\Rightarrow P=\dfrac{a}{2b+c}+\dfrac{b}{2c+a}+\dfrac{c}{2a+b}\)
\(P=\dfrac{a^2}{2ab+ac}+\dfrac{b^2}{2bc+ab}+\dfrac{c^2}{2ac+bc}\)
\(P\ge\dfrac{\left(a+b+c\right)^2}{3ab+3bc+3ca}\ge\dfrac{3\left(ab+bc+ca\right)}{3\left(ab+bc+ca\right)}=1\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
7.
\(T=\left(x^2\right)^2+\left(y^2\right)^2+\left(z^2\right)^2\ge\dfrac{1}{3}\left(x^2+y^2+z^2\right)^2\)
\(T\ge\dfrac{1}{3}\left(xy+yz+zx\right)^2=\dfrac{1}{3}\)
\(T_{min}=\dfrac{1}{3}\) khi \(x=y=z=\dfrac{1}{\sqrt{3}}\)
8.
\(S=a+b+c+ab+bc+ca\le\sqrt{3\left(a^2+b^2+c^2\right)}+a^2+b^2+c^2=6\)
\(S_{max}=6\) khi \(a=b=c=1\)
Đặt \(a+b+c=x\Rightarrow ab+bc+ca=\dfrac{\left(a+b+c\right)^2-\left(a^2+b^2+c^2\right)}{2}=\dfrac{x^2-3}{2}\)
\(\Rightarrow S=x+\dfrac{x^2-3}{2}=\dfrac{x^2+2x-3}{2}=\dfrac{\left(x+1\right)^2}{2}-2\ge-2\)
\(S_{min}=-2\) khi \(a+b+c=-1\)
Các câu hình em tự làm những ý a;b;c
6.d
Do AEPF là hình chữ nhật \(\Rightarrow PF||CD\) ; \(PE||BC\)
Talet tam giác ACD: \(\dfrac{AP}{AC}=\dfrac{AF}{AD}\)
Talet tam giác ABC: \(\dfrac{AP}{AC}=\dfrac{AE}{AB}\)
\(\Rightarrow\dfrac{AF}{AD}=\dfrac{AE}{AB}\Rightarrow EF||BD\) (Talet đảo)
Gọi G là giao điểm OQ và EF, do \(EF||BD\) theo cmt
Talet: \(\dfrac{EG}{OD}=\dfrac{QG}{OQ}\) ; \(\dfrac{FG}{OB}=\dfrac{QG}{OQ}\Rightarrow\dfrac{EG}{OD}=\dfrac{FG}{OB}\)
Mà OD=OB theo t/c hình chữ nhật \(\Rightarrow EG=FG\)
\(\Rightarrow G\) là trung điểm EF
\(\Rightarrow A;G;O\) thẳng hàng (cùng thuộc trung tuyến tam giác ABD)
Mà \(Q;G;O\) thẳng hàng \(\Rightarrow A;Q;O\) thẳng hàng
7c,d.
\(\widehat{EAH}=\widehat{FCH}\) (cùng phụ \(\widehat{ABC}\))
\(\widehat{AHE}=\widehat{CHF}\) (cùng phụ \(\widehat{AHF}\))
\(\Rightarrow\Delta AHE\sim\Delta CHF\left(g.g\right)\Rightarrow\dfrac{AE}{CF}=\dfrac{AH}{CH}=\dfrac{HE}{HF}\Rightarrow AE.CH=AH.CF\)
Đồng thời \(\Rightarrow\dfrac{HE}{AH}=\dfrac{HF}{CH}\)
\(\Rightarrow\Delta_VHEF\sim\Delta_VHAC\left(c.g.c\right)\)
Mà \(\Delta_VHAC\sim\Delta_VABC\) (chung góc C)
\(\Rightarrow\Delta_VHEF\sim\Delta_VABC\) theo tỉ số đồng dạng \(k=\dfrac{HE}{AB}\)
\(\Rightarrow S_{EHF}=k^2.S_{ABC}=\dfrac{HE^2}{AB^2}.S_{ABC}\)
Do AB và \(S_{ABC}\) cố định \(\Rightarrow S_{EHF}\) đạt min khi HE đạt min
\(\Rightarrow E\) là chân đường vuông góc hạ từ H xuống AB