X4 = 1.

Những câu hỏi liên quan
(x2-1/x2):(x2+1/x2) =a tinhsd (x4-1/x4):(x4-1/x4)
phân tích đa thức thành nhân tử
a) x4+\(\dfrac{1}{4}\)y8
b) \(\dfrac{1}{4}\)x4+y8
c) 64x4+y4
d) x4+\(\dfrac{1}{64}\)y4
Lời giải:
a.
$=(x^2)^2+(\frac{1}{2}y^4)^2+2.x^2.\frac{1}{2}y^4-x^2y^4$
$=(x^2+\frac{1}{2}y^4)^2-(xy^2)^2$
$=(x^2+\frac{1}{2}y^4-xy^2)(x^2+\frac{1}{2}y^4+xy^2)$
b.
$=(\frac{1}{2}x^2)^2+(y^4)^2+2.\frac{1}{2}x^2.y^4-x^2y^4$
$=(\frac{1}{2}x^2+y^4)^2-(xy^2)^2$
$=(\frac{1}{2}x^2+y^4-xy^2)(\frac{1}{2}x^2+y^4+xy^2)$
c.
$=(8x^2)^2+(y^2)^2+2.8x^2.y^2-16x^2y^2$
$=(8x^2+y^2)^2-(4xy)^2=(8x^2+y^2-4xy)(8x^2+y^2+4xy)$
d.
$=\frac{64x^4+y^4}{64}=\frac{1}{64}(8x^2+y^2-4xy)(8x^2+y^2+4xy)$
Đúng 1
Bình luận (0)
c: \(64x^4+y^4\)
\(=64x^4+16x^2y^2+y^4-16x^2y^2\)
\(=\left(8x^2+y^2\right)^2-\left(4xy\right)^2\)
\(=\left(8x^2+y^2-4xy\right)\left(8x^2+y^2+4xy\right)\)
Đúng 0
Bình luận (0)
Tìm giá trị của m để bất phương trình
1
-
x
4
+
1
+
x
4
+
x
4
-
2
x
2
≤
m
nghiệm đúng với
∀
m
∈
-
1
;...
Đọc tiếp
Tìm giá trị của m để bất phương trình 1 - x 4 + 1 + x 4 + x 4 - 2 x 2 ≤ m nghiệm đúng với ∀ m ∈ - 1 ; 1
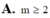
![]()
![]()
![]()
Biết x+1/x=5 .Tính x4+1/x4
D = ( x2 + x + 1)( x21 -x+1)( x4 - x2 + 1)( x8 - x4 + 1)
Bạn cần viết đầy đủ đề: Bao gồm yêu cầu đề và công thức toán để được hỗ trợ tốt hơn.
Đúng 0
Bình luận (0)
\(D=\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=\left[\left(x^2+1\right)^2-x^2\right]\left(x^4-x^2+1\right)\left(x^8-x^4+1\right)\)
\(=\left(x^4+x^2+1\right)\left(x^4-x^2+1\right)\cdot\left(x^8-x^4+1\right)\)
\(=\left(x^8+2x^4+1-x^4\right)\left(x^8-x^4+1\right)\)
\(=\left(x^8+1\right)^2-x^8\)
\(=x^{16}+x^8+1\)
Đúng 0
Bình luận (0)
Thực hiện phép tính g) (x + 2)(1 + x - x2 + x3 - x4) - (1 - x)(1 + x +x2 + x3 + x4); a) (x + 1)(1 + x - x2 + x3 - x4) - (x - 1)(1 + x + x2 + x3 + x4); b) ( 2b2 - 2 - 5b + 6b3)(3 + 3b2 - b); c) (4a - 4a4 + 2a7)(6a2 - 12 - 3a3); d) (2ab + 2a2 + b2)(2ab2 + 4a3 - 4a2b) e) (2a3 - 0,02a + 0,4a5)(0,5a6 - 0,1a2 + 0,03a4).
\(a,=x+x^2-x^3+x^4-x^5+1+x-x^2+x^3-x^4-x-x^2+x^3-x^4+x^5+1+x-x^2+x^3-x^4\\ =2x-2x^2+2x^3-2x^4\)
Đúng 3
Bình luận (0)
1) x4 - 8x2 + 4x + 3 = 0
2) x4 - 3x3 - 7x2 + 24x - 8 = 0
3) x4 - x3 - x2 + x + 1 = 0
Giải phương trình??? sử dụng Hooc-ne cho nhanh nhá :v
1) \(x^4-8x^2+4x+3=0\)
( dùng máy tính ta đoán được 1 nghiệm chính xác là -3 )
\(\Leftrightarrow\left(x+3\right)\left(x^3-3x^2+x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^3-3x^2+x+1=0\left(2\right)\end{matrix}\right.\)
Tiếp tục dùng máy tính ta tìm được 1 nghiệm chính xác của pt ( 2 ) là 1
\(\Leftrightarrow\left(x+3\right)\left(x-1\right)\left(x^2-2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-1=0\\x^2-2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\\x=1+\sqrt{2}\\x=1-\sqrt{2}\end{matrix}\right.\)
rồi mấy câu còn lại tương tự
Đúng 1
Bình luận (0)
cho 5 số:x1,x2,x3,x4,x5 mỗi số =1 hoặc = -1.Chứng minh: x1.x2+x2.x3+x3.x4+x4.x5+x5.x1 khác 0
x1;x2;x3;x4;x5=-1 hoặc 1
=>x1.x2;x2.x3;x3.x4;x4.x5;x5.x1 bằng 1 hoặc -1
giả sử x1.x2+x2.x3+x3.x4+x4.x5+x5.x1=0
=>số các số hạng 1 và -1 bằng nhau
=>số các số hạng chia hết cho 2
=>5 chia hết cho 2(có 5 số hạng) Vô lí
=>x1.x2+x2.x3+x3.x4+x4.x5+x5.x1\(\ne0\)
=>đpcm
Đúng 0
Bình luận (0)
chtt
ai làm ơn tích mình ,mình tích lại cho
Đúng 0
Bình luận (0)
x1x2+x2x3+x3x4+x4x5+x5x1=[(x2)*2]+[(x2)*6]+[(x2)*12]+[(x2)*20]+[(x2)*5]=(x2)*(2+6+12+20+5)
Mà x2 là số dương và 2+6+12+20+5 cũng là số dương nên x1x2+x2x3+x3x4+x4x5+x5x1 khác 0
tick nha
Đúng 0
Bình luận (0)
cm pt vô nghiệm
a)x4 +x3 +1=0
b)x4+x+1=0
a.
\(x^4+x^3+1=\left(\dfrac{x^4}{4}+x^3+x^2\right)+\left(\dfrac{3x^4}{4}-x^2+\dfrac{1}{3}\right)+\dfrac{2}{3}\)
\(=\left(\dfrac{x^2}{2}+x\right)^2+\dfrac{3}{4}\left(x-\dfrac{2}{3}\right)^2+\dfrac{2}{3}>0\) ; \(\forall x\)
\(\Rightarrow x^4+x^3+1=0\) vô nghiệm
b.
\(x^4+x+1=\left(x^4-x^2+\dfrac{1}{4}\right)+\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{1}{2}\)
\(=\left(x^2-\dfrac{1}{2}\right)^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{2}>0\) ; \(\forall x\)
\(\Rightarrow x^4+x+1=0\) vô nghiệm
Đúng 1
Bình luận (0)
Lời giải:
a.
$2(x^4+x^3+1)=2x^4+2x^3+2=(x^4+2x^3+x^2)+x^4-x^2+1$
$=(x^2+x)^2+(x^2-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow x^4+x^3+1>0, \forall x\in\mathbb{R}$
Do đó pt $x^4+x^3+1=0$ vô nghiệm.
b.
$x^4+x+1=(x^4-x^2+\frac{1}{4})+(x^2+x+\frac{1}{4})+\frac{1}{2}$
$=(x^2-\frac{1}{2})^2+(x+\frac{1}{2})^2+\frac{1}{2}\geq \frac{1}{2}>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow x^4+x+1=0$ vô nghiệm (đpcm).
Đúng 1
Bình luận (0)
g) (x + 2)(1 + x - x2 + x3 - x4) - (1 - x)(1 + x +x2 + x3 + x4);
\(=x+x^2-x^3+x^4-x^5+2+2x-2x^2+2x^3-2x^4-\left(1+x+x^2+x^3+x^4-x-x^2-x^3-x^4-x^5\right)\\ =2+3x-x^2+x^3-x^4-x^5-1\\ =-x^5-x^4+x^3-x^2+3x+1\)
Đúng 1
Bình luận (0)























