a) ĐKXĐ:

x³ - 1 khác 0

x khác 1

b) A = (5x² + 5x + 5)/(x³ - 1)

= 5(x² + x + 1)/[(x - 1)(x² + x + 1)]

= 5/(x - 1)

Thay x = 7 vào A, ta được:

A = 5/(7 - 1)

= 5/6

I.

1 D

2 B

3 D

4 A

5 C

6 A

7 A

8 C

II.

1 am listening

2 Are you playing

3 am reading/is watching

4 is cooking

5 is riding

II.

1 am listening (keep silent! . DHNB thì HTTD)

2 Are you playing ( now : DHNB thì HTTD)

3 am reading/is watching ( at the moment )

4 is cooking (at the moment  DNNB thì HTTD)

5 is riding ( look)

I.

1.A

2.D

3.D

4.A

5.C

6.A

7.A

8.C

II.

1.am listening

2.Are you playing

3.am reading

4.is cooking

5.is riding

1 A

2 C

3 D

4 A

5 D

6 B

7 C

8 C

9 B

10 B

11 A

12 B

13 D

14 B

15 B

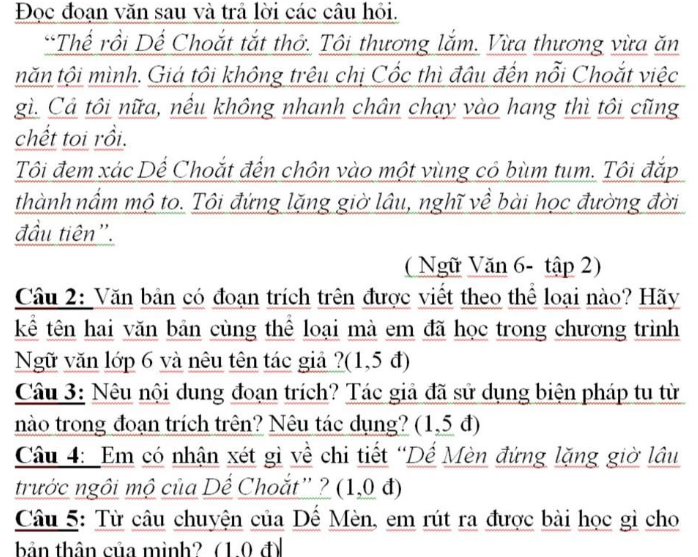
2. Thể loại truyện dài

2 tác phẩm cùn thể loại là: Sông nước Cà Mau (Đoàn Giỏi) và Vượt thác (Võ Quảng)

3. 

Tham khảo nha em:

- Dế Mèn tự tả chân dung.

- Dế Mèn trêu chị Cốc dẫn đến cái chết của Dế Choắt. Dế Mèn ân hận rút ra bài học đường đời đầu tiên.

4. Dế Mèn hối hặn vì sự nông nổi, dại dột của mình đã gây ra cái chết cho Dế Choắt và rút ra bài học cho bản thân

5. 

Tham khảo nha em:

- Qua sự việc ấy, Dế Mèn đã rút ra được bài học đường đời đầu tiên cho mình. Đó là: Không được kiêu căng, tự phụ. Không được cậy vào sức khỏe của mình mà hung hăng làm bậy. Nếu không suy nghĩ cẩn thận trước khi làm sẽ mang họa vào thân.

a. \(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\Rightarrow sin^2x+cos^2x+2sinx.cosx=\dfrac{1}{25}\)

\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)

\(P=tanx+cotx=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)

b. \(\left(tana-cota\right)^2=\left(2\sqrt{3}\right)^2\Leftrightarrow\left(tana+cota\right)^2-4tana.cota=12\)

\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)

\(\Rightarrow\left|tana+cota\right|=4\)

a, - 1 ≤ cosx ≤ 1 ⇔ - 1 ≤ - cosx ≤ 1 

⇔ 4 ≤ 5 - cosx ≤ 6

⇔ 4 ≤ y ≤ 6.

Vậy y_min = 4 khi cosx = 1 ⇔ x = k2π

y_max = 6 khi cosx = - 1 ⇔ x = π + k2π

b, - 1 ≤ sinx ≤ 1 ⇔ - 4 ≤ 4sinx ≤ 4

⇔ - 3 ≤ 4sinx + 1 ≤ 5 ⇔ - 3 ≤ y ≤ 5

y_min = - 3 khi sinx = - 1

y_max = 5 khi sinx = 1

c, sinx - cosx + 7

= \(\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)\) + 7

min = 7 - \(\sqrt{2}\) và max = 7 + \(\sqrt{2}\)

d, Đặt cosx = t ta có hàm số f(t) = 3t² + t - 2 với t ϵ [- 1 ; 1]

Dùng BBT của hs bậc 2 là được

e, chuyển sin²x = 1 - cos²x

f, \(\sqrt{3}sinx-cosx=2sin\left(x-\dfrac{\pi}{6}\right)\)

g, \(sinx+\sqrt{3}cosx=2sin\left(x+\dfrac{\pi}{3}\right)\)

h, Đặt a = arcsin\(\dfrac{4}{5}\) = arcsin\(\dfrac{3}{5}\)

⇒ 3sinx + 4cosx = 5 sin (x + a) với a = arcsin\(\dfrac{4}{5}\) = arcsin\(\dfrac{3}{5}\)

i, 2sin²x - 1 = - cos2x

k, 7 - 2sin²x . cosx = 7 - (1- cos2x) . cosx

= 7 + cos2x . cosx - cosx 

= 7 + \(\dfrac{1}{2}cos3x+\dfrac{1}{2}cosx-cosx\)

= 7 + \(\dfrac{1}{2}cos3x-\dfrac{1}{2}cosx\)

Ta có - 1 ≤ cos3x ≤ 1; -1 ≤ - cosx ≤  1

nên cos3x - cosx ∈ [- 2 ; 2]

Từ đó suy ra min max. Dấu bằng có xảy ra

Tham khảo bài sau nhé:

https://mathx.vn/hoi-dap-toan-hoc/142780.html

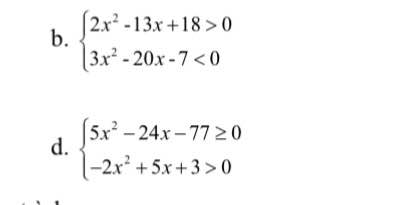
b.

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 2\\x>\dfrac{9}{2}\end{matrix}\right.\\-\dfrac{1}{3}< x< 7\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}-\dfrac{1}{3}< x< 2\\\dfrac{9}{2}< x< 7\end{matrix}\right.\)

Hay \(S=\left(-\dfrac{1}{3};2\right);\left(\dfrac{9}{2};7\right)\)

d.

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le-\dfrac{11}{5}\\x\ge7\end{matrix}\right.\\-\dfrac{1}{2}< x< 3\end{matrix}\right.\) \(\Rightarrow x\in\varnothing\) hay BPT vô nghiệm