Tham Khảo e nhá chj ngu ném ko bik làm☹

https://hoc24.vn/cau-hoi/cho-tam-giac-abc-m-la-trung-diem-bc-chung-minh-ab2-ac2-2am2-bc22.249563555147

Kẻ AH vuông góc BC.

Xét tam giác AHM vuông tại H (^AHM = 90⁰) có:

AM² = AH² + HM² (định lý Pytago).

Xét tam giác AHB vuông tại H (^AHB = 90⁰) có:

AB² = AH² + BH² (định lý Pytago).

Xét tam giác AHC vuông tại H (^AHC = 90⁰) có:

AC² = AH² + CH² (định lý Pytago).

Ta có: BH = BM - HM.

          CH = CM + HM. 

Vì M là trung điểm của BC (gt) => BM = CM; BM = \(\dfrac{BC}{2}\) => BM² = \(\dfrac{BC^2}{4}\).

Ta có: AB² + AC² = AH² + BH² + AH² + CH².

          AB² + AC² = AH² + AH² + BH² + CH².

                            = 2AH² + (BM - HM)² + (CM + HM)².

                            = 2AH² + BM² - 2BM.HM + HM² + CM² + 2CM.HM + HM².

                            = 2AH² + BM² - 2BM.HM + HM² + BM² + 2BM.HM + HM².

                            = 2AH² + 2HM² + 2BM².

                            = 2(AH² + HM²) + 2\(\dfrac{BC^2}{4}\).

          AB² + AC² = 2AM² + \(\dfrac{BC^2}{2}\) (đpcm). 

a, Sử dụng định lí Pytago cho các tam giác vuông HAB và HAC để có đpcm

b, 1. Chứng minh tương tự câu a)

2. Sử dụng định lí Pytago cho tam giác vuông AHM

Xét ΔABC có 

M là trung điểm của AB

N là trung điểm của AC

Do đó:MN là đường trung bình

=>MN//BC và MN=BC/2

Áp dụng HTL: \(AB^2=BH.BC;AC^2=CH.BC\)

\(\Leftrightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}=\dfrac{BH}{CH}\)

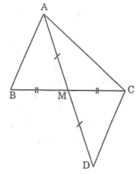
Trên tia đối của tia MA lấy điểm D sao cho MA = MD.

Xét ΔAMB và ΔDMC, ta có:

MA = MD (theo cách vẽ)

∠(AMB) = ∠(DMC) (đối đỉnh)

MB = MC (gt)

Suy ra: ΔAMB = ΔDMC (c.g.c)

Suy ra: AB = CD (hai cạnh tương ứng)

Trong ΔACD, ta có: AD < AC + CD

(bất đẳng thức tam giác)

Suy ra: AD < AC + AB

Mà AD = AM + MD = 2AM

Suy ra: 2AM < AC + AB hay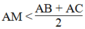 

Câu 20: Tam giác ABC vuông tại B suy ra:

   A.  AC²  = AB² + BC^{2 ­}                                   B.  AC²  = AB² - BC²

   C.  BC²  = AB² + AC²                                    D.  AB²  = BC² + AC²

Câu 21: Tam giác ABC có BC = 5cm; AC = 12cm; AB = 13cm. Tam giác ABC vuông tại đâu?

   A.  Tại  B                                                      B.  Tại C

   C.  Tại A                                                       D.  Không phải là tam giác vuông

Câu 22: Cho ABC có  = 90⁰ ; AB = 4,5 cm ; BC = 7,5 cm. Độ dài cạnh AC là:

   A.  6,5 cm                    B.  5,5 cm                     C.  6 cm                       D.   6,2 cm

Câu 23: Tam giác nào là tam giác vuông trong các tam giác có độ dài các cạnh là:

A.  3cm, 4dm, 5cm.         B.  5cm, 14cm, 12cm. 

C.  5cm, 5cm, 8cm.         D.  9cm, 15cm, 12cm.

Câu 24: Cho ABC có  AB = AC và  = 60⁰, khi đó tam giác ABC là:

   A.  Tam giác vuông                                       B.   Tam giác cân

   C.  Tam giác đều                                           D.  Tam giác vuông cân

Câu 25: Nếu A là góc ở đáy của một tam giác cân thì:

A.  ∠A ≤ 90⁰                                 B. ∠A > 90⁰                            C. ∠A < 90⁰                       D. ∠A = 90⁰

Bài 9:

1: Xét ΔABC có

E,K lần lượt là trung điểm của AB,AC

=>EK là đường trung bình của ΔABC

2: Vì EK là đường trung bình của ΔABC

nên EK//BC và \(EK=\dfrac{1}{2}BC\)

=>EI//BH

Xét ΔABH có

E là trung điểm của AB

EI//BH

Do đó: I là trung điểm của AH

3: \(EK=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot10=5\left(cm\right)\)

bài 10:

1: Xét ΔADC có

M là trung điểm của AD

MN//DC

Do đó: N là trung điểm của AC

Xét hình thang ABCD có

M là trung điểm của AD

MK//AB//CD

Do đó: K là trung điểm của BC

2: \(AB=\dfrac{1}{2}DC=\dfrac{1}{2}\cdot20=10\left(cm\right)\)

Xét ΔADC có

M,N lần lượt là trung điểm của AD,AC

=>MN là đường trung bình của ΔADC

=>\(MN=\dfrac{DC}{2}=10\left(cm\right)\)

Xét ΔCAB có

N,K lần lượt là trung điểm của CA,CB

=>NK là đường trung bình của ΔCAB

=>\(NK=\dfrac{1}{2}AB=5\left(cm\right)\)

MK=MN+NK

=10+5

=15(cm)